 統計学的検定:共通の平均の検定; tmean
統計学的検定:共通の平均の検定; tmean
統計学の分野では,すべてのデータの集合を母集団,そこからランダムに取り出した幾つかのデータを標本とよびます.母集団についてのある特性を知りたい場合は,標本についてその特性を測定し,その測定結果に基づいて母集団の特性を結論づけます.以後,平均,標準偏差,分散を,標本については, \(\bar x\), \(s\), \(s\)\(^2\),母集団については, \(\mu\), \(\sigma\), \(\sigma\)\(^2\) と記します.統計学的検定では,標本の測定から計算されたある量(統計量)が,ある既知の分布に従うという定理(命題)を使用します.よく知られている例としては,正規分布(ガウス分布)に従う母集団から得られた \(n\) 個のデータの平均, \(\bar x=\frac{1}{n}\sum_{i=1}^n x_i\),の分布も正規分布となり,その平均は \(\mu\) で分散は \(\sigma^2/n\) となるという定理があります.このよく知られた定理でさえ,統計学の教科書が詳細に記述することから分かるように,その証明は難解です.しかし,統計学的検定を応用する者としては,定理の正当性を単に信じれば,検定を実行することは容易です.
共通の平均の検定
プログラム "tmean" は,スカラー・データの2つの標本が1つの母集団平均を共有するかを検定します.プログラムは母集団の分散が等しい場合は Student's \(t\)-test を,等しくないときは Welch's \(t\)-test を実行します.標本1のデータ数,平均,分散を \(n_1\), \(\bar x_1\), \(s_1^2\) とし,標本2については \(n_2\), \(\bar x_2\), \(s_2^2\) と記すこととします.ここで,次の帰無仮説を設定します. \begin{equation} \mu_1 - \mu_2 = 0. \nonumber \end{equation} この仮説のもとでは,母集団の分散が等しいときは(student's \(t\)-test),次の統計量 \(t\) は自由度が \(\nu = n_1 + n_2 - 2\) の \(t\)-分布に従います. \begin{equation} t = \frac{\bar x_1 - \bar x_2}{s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}, \label{eq01} \end{equation} ここに, \begin{equation} s_p^2 = \frac{s_1^2(n_1-1) + s_2^2(n_2-1)}{n_1 + n_2 - 2}, \label{eq02} \end{equation} はプールした分散(合成分散)です.母集団の分散が等しくないときは(Welch's \(t\)-test),次の統計量 \(t\) が \(t\)-分布に従い, \begin{equation} t = \frac{\bar x_1 - \bar x_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}, \label{eq03} \end{equation} 自由度 \(\nu\) は, \begin{equation} \nu = \frac{ \left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2 }{ \frac{s_1^4}{n_1^2(n_1-1)} + \frac{s_2^4}{n_2^2(n_2-1)} }, \label{eq04} \end{equation} で与えられますが,これは必ずしも整数ではありません.検定を実行するには,観測結果から \eqref{eq01} または \eqref{eq03} を使用して \(t\) を計算します.有意水準を \(\alpha\) として,もし \(t\) が \(t\)-分布の下方 \(\alpha/2\) 点より小さいか,上方 \(\alpha/2\) 点より大きい場合(両側検定),帰無仮説は棄却され,2つの母集団の平均は異なると結論します.下図は典型的な \(t\)-分布曲線(\(\nu=5\))で, \(\alpha\)=5% での棄却域を赤色で示しています.
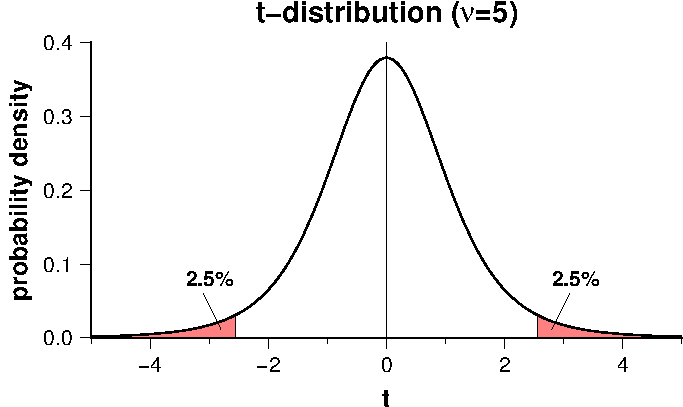
共通の分散の検定
上で示した共通の平均の検定を行う前に,2つの母集団が共通の分散を有するかを知る必要があります.この目的には,次の帰無仮説を設定して, \(F\) 検定を実施します. \begin{equation} \frac{\sigma_1^2}{\sigma_2^2} = 1. \nonumber \end{equation} この仮説のもとでは,2つの標本分散の比, \begin{equation} F = \frac{s_1^2}{s_2^2}, \label{eq05} \end{equation} は \(F\) 分布に従い,自由度は次式で与えられます. \begin{equation} \nu_1 = n_1 - 1, \quad \nu_2 = n_2 - 1, \label{eq06} \end{equation} ここに, \(n_1\) と \(n_2\) はそれぞれ標本1と2に含まれるデータ数です.もし観測結果から得られた統計量 \(F\) が規定の有意水準 \(\alpha\) に対応する上下の基準値より大きいか小さい場合は,帰無仮説は棄却されます.実際には,より大きい分散を\eqref{eq05}の分子に取り,常に \(F\) が1よりも大きいようにして計算します.もし \(F\) が上方 \(\alpha/2\) 点より大きければ帰無仮説は棄却されます.ここで注意点として,次のような誤った記述を含む教科書があることを指摘します:『常に \(F\) は1より大きいので,上方 \(\alpha/2\) 点ではなく,上方 \(\alpha\) 点を使用します』.これは誤りで,常に \(F\)>1 を取るのは \(F\)<1 の範囲の \(F\) 分布表がないための便宜的な手段だからです.原理的には,計算だけに頼れば \(F\) の事前の操作は不要です.下図に示すのは, \(\nu_1\)=10, \(\nu_2\)=20 の \(F\) 分布の下方 2.5% 点(0.2925)が, \(\nu_1\)=20, \(\nu_2\)=10 の \(F\) 分布の上方 2.5% 点(3.4185)の逆数となっていることです.
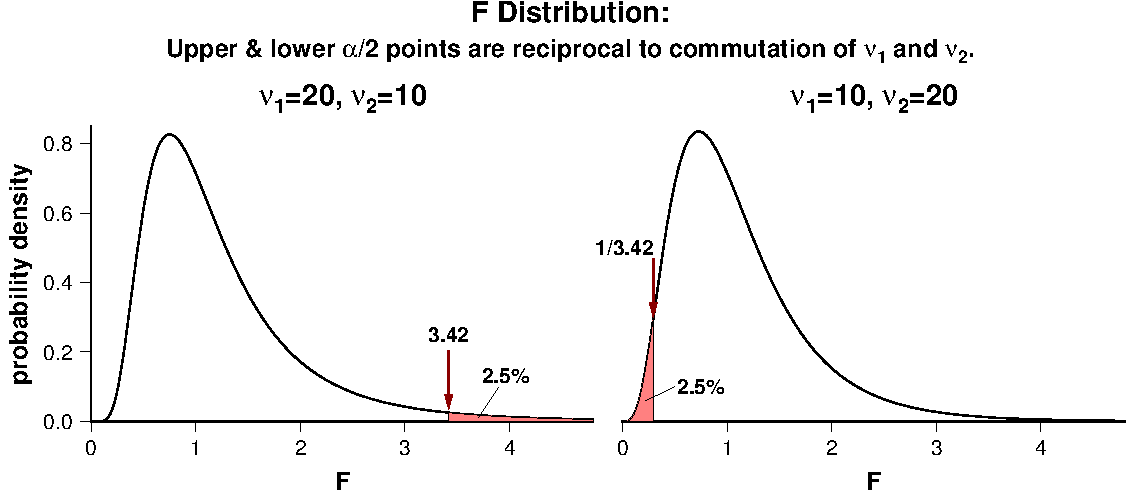
もし共通の母集団分散が棄却されたら,2つの母集団の分散は異なると結論し, Welch's \(t\)-test を使用して,共通の平均の検定を実行します.そうでなければ, Student's \(t\)-test が使用されます.ここで後者では,避けることのできない問題が生じます.それは帰無仮説が棄却されない場合には,我々は分散の差については何も言うことはできないからです.2つの母集団の分散が等しいと主張することはできません.帰無仮説が棄却されなかった理由は,少ないデータ数かもしれないし,大きい誤差かもしれません.それでも我々は, \(F\) 検定の結果は等しい分散と矛盾するわけではないとして, Student's \(t\)-test の実行に進みます.この状況は古地磁気学における逆転テストの正の結果と似ています.
プログラムのダウンロードとインストール
\(t\)-分布と \(F\) 分布で使用される関数の概要
以下, \(f(x)\) は \(x\) の確率密度で \(P(x_c)\) は \(x\) が基準値 \(x_c\) を超える確率です.定義や表記は次のマニュアルや教科書を参考にしています: Crow et al. (1960), 小針 (1973), Press et al. (1992).
\(t\)-分布:
\begin{eqnarray} f(t) & = & \frac{\Gamma({\nu+1 \over 2})}{\sqrt{\nu}\Gamma({\nu \over 2})\Gamma({1 \over 2})}\left(1+{t^2 \over \nu}\right)^{-{\nu+1 \over 2}}, \nonumber \\ & = & \frac{1}{\sqrt{\nu}B({\nu \over 2},{1 \over 2})}\left(\frac{\nu}{\nu+t^2}\right)^{{\nu+1 \over 2}}, \label{eq07} \end{eqnarray} ここに, \[ \Gamma(z) = \int_0^\infty u^{z-1}e^{-u} du, \] はガンマ関数で, \(z\) が整数のときは階乗(ファクトリアル)関数(\(\Gamma(n+1)=n!\))になります.また, \(\Gamma(1/2)=\sqrt{\pi}\) という関係もあります.式 \eqref{eq07} の \(B(\nu/2,1/2)\) はベータ関数であり, \[ B(z,w) = B(w,z) = \int_0^1 u^{z-1}(1-u)^{w-1} du, \] で与えられ,ガンマ関数とは次式のように関係しています. \[ B(z,w) = \frac{\Gamma(z)\Gamma(w)}{\Gamma(z+w)}. \] 式 \eqref{eq07} の \(f(t)\) を積分して, \[ P(t) = \int_t^\infty f(t)dt = \frac{1}{\sqrt{\nu}B({\nu \over 2},{1 \over 2})}\int_t^\infty \left(\frac{\nu}{\nu+t^2}\right)^{{\nu+1 \over 2}}dt. \] 次のように変数変換をすると, \[ z = \frac{\nu}{\nu+t^2}, \quad dt = -\frac{\sqrt{\nu}}{2}z^{-{3 \over 2}}(1-z)^{-{1 \over 2}}dz, \] \(P(t)\) は次式となります. \begin{eqnarray} P(t) & = & \frac{1}{2 B({\nu \over 2},{1 \over 2})}\int_0^{\nu \over \nu+t^2}z^{{\nu \over 2}-1}(1-z)^{{1 \over 2}-1}dz, \nonumber \\ & = & \frac{1}{2}I_{{\nu \over \nu+t^2}}\left({\nu \over 2},{1 \over 2}\right), \label{eq08} \end{eqnarray} ここに, \[ I_x(a,b) = \frac{1}{B(a,b)}\int_0^x z^{a-1}(1-z)^{b-1} dz \quad (a,b > 0), \] は不完全ベータ関数です.与えられた確率 \(P_c\) に対応する \(t_c\) を決定するためには,次のように Press et al. (1992) の関数 "rtsafe" を用いて, \eqref{eq08} を方程式として数値計算で解きます. \[ P_c - (1/2)I_{\nu/(\nu+t_c^2)}(\nu/2,1/2) = 0. \]
\(F\) 分布:
\begin{eqnarray} f(F) & = & \frac{\Gamma({\nu_1+\nu_2 \over 2})}{\Gamma({\nu_1 \over 2})\Gamma({\nu_2 \over 2})} \frac{\nu_1^{\nu_1 \over 2} \nu_2^{\nu_2 \over 2} F^{\nu_1-2 \over 2}}{(\nu_2+\nu_1 F)^{\nu_1+\nu_2 \over 2}} \quad (F ≥ 0), \nonumber \\ & = & \frac{1}{B({\nu_1 \over 2},{\nu_2 \over 2})} \frac{\nu_1^{\nu_1 \over 2} \nu_2^{\nu_2 \over 2} F^{\nu_1-2 \over 2}}{(\nu_2+\nu_1 F)^{\nu_1+\nu_2 \over 2}} \quad (F ≥ 0). \label{eq09} \end{eqnarray} これを積分すると次式を得ます. \[ P(F) = \int_F^\infty f(F)dF = \frac{1}{B({\nu_1 \over 2},{\nu_2 \over 2})} \int_F^\infty \frac{\nu_1^{\nu_1 \over 2} \nu_2^{\nu_2 \over 2} F^{\nu_1-2 \over 2}}{(\nu_2+\nu_1 F)^{\nu_1+\nu_2 \over 2}} dF. \] 次のように変数変換して, \[ z = \frac{\nu_2}{\nu_2+\nu_1 F}, \quad dF = -\frac{\nu_2}{\nu_1}\frac{1}{z^2} dz, \] \(P(F)\) は次式で表されます. \begin{eqnarray} P(F) & = & \frac{1}{B({\nu_2 \over 2},{\nu_1 \over 2})} \int_0^{{\nu_2 \over \nu_2+\nu_1 F}}z^{{\nu_2 \over 2}-1}(1-z)^{{\nu_1 \over 2}-1} dz, \nonumber \\ & = & I_{\nu_2 \over \nu_2+\nu_1 F}\left({\nu_2 \over 2},{\nu_1 \over 2}\right). \label{eq10} \end{eqnarray} 与えられた確率 \(P_c\) に対応する \(F_c\) を求めるには,次のように Press et al. (1992) の関数 "rtsafe" を用いて, \eqref{eq10} を方程式として数値計算で解きます. \[ P_c - I_{\nu_2/(\nu_2+\nu_1 F_c)}(\nu_2/2,\nu_1/2) = 0. \]
参考文献:
- Crow, E. L., F. A. Davis, and M. W. Maxfield, Statistics Manual, 288 pp., Dover Pub. Inc., New York, 1960.
- 小針アキ宏, 確率・統計入門, 300 pp., 岩波書店, 東京, 1973.
- Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery, Numerical Recipes in C: The Art of Scientific Computing (Second Edition), 994 pp., Cambridge University Press, Cambridge, 1992.