問題３−３−１ 解答

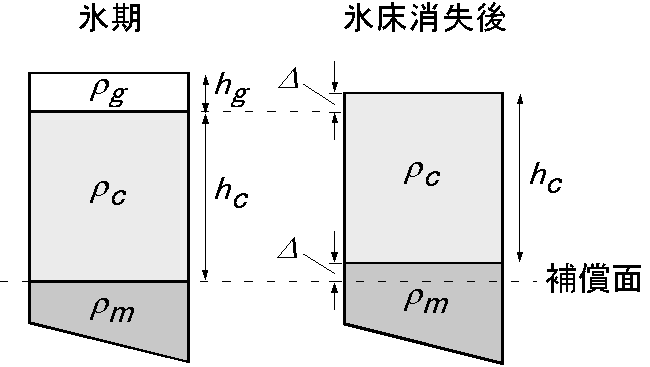
図のように補償面を氷期の沈んだ地殻の底面に取り，補償面での圧力を等しいとおくと， \[ \rho_g h_g + \rho_c h_c = \rho_c h_c + \rho_m \mit\Delta. \] となり，次の２式を得ます． \[ h_g = \frac{\rho_m}{\rho_g}\mit\Delta, \quad \mit\Delta = \frac{\rho_g}{\rho_m}h_g. \]

（１） 計算結果は，\(h_g = 1100\ \mathrm{m} \approx 1\ \mathrm{km}\).

（２） \(\mit\Delta\) の計算結果は 681.8 m となります．約 680 m 隆起すると，南極大陸も特に異常ではない平均高度になります．

問題３−３−２ 解答

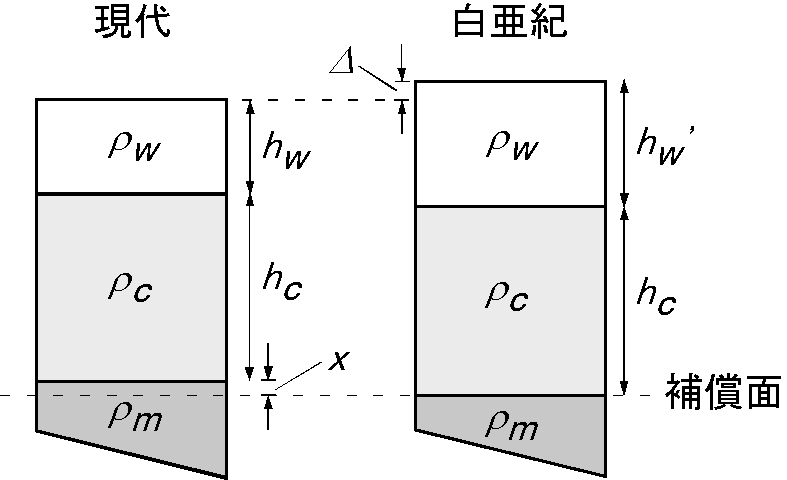
図のように補償面を白亜紀の沈んだ地殻の底面に取ります．地殻の沈み量は現代の地殻の底面の補償面からの高さとなりますが，これを \(x\) とします．高さの明らかな関係 \[ \mit\Delta + h_w + h_c + x = h_w^\prime + h_c, \] より， \[ x = h_w^\prime - h_w - \mit\Delta. \] 補償面での圧力を等しいとおいて， \[ \rho_w h_w + \rho_c h_c + \rho_m x = \rho_w h_w^\prime + \rho_c h_c. \] これに上の \(x\) を代入して変形します． \begin{eqnarray*} \rho_w h_w + \rho_m(h_w^\prime - h_w - \mit\Delta) & = & \rho_w h_w^\prime, \\ \rho_m(h_w^\prime - h_w) - \rho_m\mit\Delta & = & \rho_w(h_w^\prime - h_w), \\ (\rho_m - \rho_w)(h_w^\prime - h_w) & = & \rho_m\mit\Delta. \end{eqnarray*} よって， \[ h_w^\prime - h_w = \frac{\rho_m}{\rho_m - \rho_w}\mit\Delta. \] この式に， \(\mit\Delta\) = 200 m， \(\rho_w\) = 1000 kg/m³， \(\rho_m\) = 3300 kg/m³ を代入して， \[ h_w^\prime - h_w = \frac{3300}{3300-1000}\times 200 = 287\ \mathrm{m}. \]

問題３−３−３ 解答

計算結果は以下の通りです．

\(Ra\) は 1000 を超え，マントルは対流していると考えられます．

→ ホーム