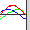
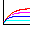
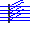
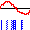
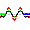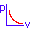位相速度と群速度

\[ y=A\sin(kx-ωt) \] \[ y'=A\sin(k'x-ω't) \]

を重ね合わせると

\[ y+y'=2A\cos(\frac{k'-k}{2}x-\frac{ω'-ω}{2}t)\sin(\frac{k'+k}{2}x-\frac{ω'+ω}{2}t) \] \[ \approx2A\cos(\frac{k'-k}{2}x-\frac{ω'-ω}{2}t)\sin(kx-ωt) \]

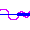
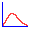
\(k'\approx k\)のとき、上の式の第一因子はゆっくり変化するので第二因子の波の振幅のようなものであり、この振幅の0と0の間が波束である。この振幅が最大の点は

\[ \frac{k'-k}{2}x-\frac{ω'-ω}{2}t=0 \] より、群速度\(Vg\)は

\[ Vg=\frac{ω'-ω}{k'-k}=\frac{dω}{dk} \]

位相速度\(Vp\)は第二因子より

\[ Vp=\frac{ω'+ω}{k'+k}\approx\frac{ω}{k} \]