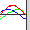
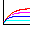
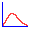
(random walk によって1次元正規分布で広がる酔っ払い) drunk

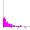
一直線上の酔っ払い、または、拡散シミュレーション(参考：米沢富美子「ブラウン運動」共立出版　p.12)
原点からの変位の二乗の平均値を s^2 とし、その平方根を s とする。十分時間が経つと、s^2 は時間 t に比例するらしい。(左下の計算で、s^2 / t = 一定値に近づいていく。)　 よって、s は √t に比例する。つまり、右往左往する酔っ払い達の出発点からの平均のずれは時間 t の平方根に比例して増加する。規格化されたガウス分布曲線を -s から s まで積分(数値解析)すると 0.6826 くらいになる。この範囲の酔っ払いの人数をコンピューターで数え上げると左下のように、実際、6800 人くらいになってる。