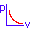ドーム球場の設計 京都大2000年度後期試験
「最大の初速度Vで、あらゆる方向に打ち分けることができる最強の打者を想定して、ドーム球場の屋根を設計せよ。」javaScript表示 download(HTML5+javaScript)zip
ボールの初速度の向きが水平となす角度を \( \theta \) とすると、時刻 \( t \) でのボールの座標 \( x \)、\( y \) は
\[ x = Vt\cos\theta \] \[ y = Vt\sin\theta - \frac{1}{2}gt^2 \]これらの式から \( t \) を消去して、ボールの軌跡を表す式を求めると
\[ y = x\tan\theta - \frac{1}{2} g \left( \frac{x}{V\cos\theta} \right)^2 \]\(\tan\theta = a\) と置くと、\( x = X \) でのボールの高さ \( y \) は
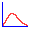
\[ y =\frac{gX^2}{2V^2}(a-\frac{V^2}{gX})^2+\frac{V^2}{2g}-\frac{gX^2}{2V^2} \]よって\( x=X \)でのボールの高さ\(y\)の最大値\(Y\)は
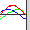
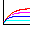
\[ Y=\frac{V^2}{2g}-\frac{gX^2}{2V^2} \]これがボールの無数の放物線の包絡線を表す式であり、ドームの屋根の形状は上の放物線の回転体である