その他： X-Y データの円近似； pcirc

プログラム "pcirc" は Taubin (1991) の方法で２次元 X-Y データ（N≥3）の円近似を実行し，近似された円のポストスクリプトによる図を描きます．この方法は，"代数学的"距離 \(r_i^2-R^2\) の二乗の合計を最小にするような円のパラメータを探すのであり，"幾何学的"距離 \(r_i-R\) については考慮しません．ここに， \(r_i\) と \(R\) はそれぞれデータ点の円中心からの距離と円の半径です．代数学的方法は幾何学的方法より正確さは劣りますが，前者は速い計算速度のために実践的です．理論の簡単な解説は → このページにあります． "pcirc" のプログラム・コードは Chernov (2012) による C++ ルーチンを C 言語用に変更しました．

円近似の例

次の例で使用するデータのファイル test.d には４つの点 (1.1, 0), (0, 0.9), (-1.1, 0), (0, -0.9) が含まれています．これらのデータに円近似を実行するには次のようにタイプします．

pcirc test.d -c -l

ここに "-C" と "-L" はそれぞれ円中心のプロットと画面に入力データを表示するオプションです．円近似の結果は次のように表示されます．

Circle fitting of test.d
  PS file: test.ps
   N     X0         Y0         R          k          SSE
  4    0.000      0.000      1.005      0.000      0.04010  
  Input data:
    i   X          Y          Error
    1  1.100      0.000      0.09501  
    2  0.000      0.9000    -0.1050   
    3 -1.100      0.000      0.09501  
    4  0.000     -0.9000    -0.1050

ここに "(X0,Y0)" と "R" はそれぞれ近似された円の中心と半径です． "k" と "SSE" はそれぞれ曲率を表すパラメータと， \(r_i-R\) で表される誤差の２乗の合計です．これらは古地磁気強度データの評価に使用され，一般のデータには不要です（"pmagm302.tar.gz" に含まれる "MEMOS_pmagm302.pdf" を参照してください）．下図は出力されたポストスクリプト・ファイル "test.ps" です．

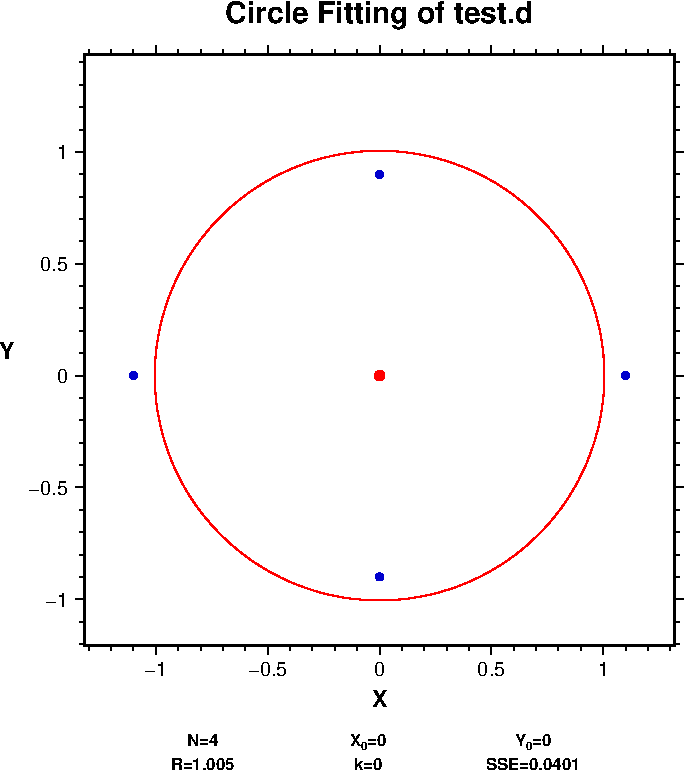
注意すべき点として，半径 R が本来の値 1 よりも僅かに大きいことです．前述したように，代数学的方法は幾何学的方法よりも正確さは劣ります．それは前者では， "\(r_i - R\)" ではなく "\(r_i^2 - R^2\)" の二乗の合計を最小にするからです．しかしながら，前者はアルゴリズムがより単純で計算速度も速いため広く使用されています．

プログラムのダウンロードとインストール

→ このページにあります．

参考文献：

Chernov, N, Fitting ellipses, circles, and lines by least squares, 2012. (URL: →http://people.cas.uab.edu/~mosya/cl/ index.html)
Taubin, G., Estimation of planar curves, surfaces and nonplanar space curves defined by implicit equations, with applications to edge and range image segmentation, IEEE Trans. Pattern Analysis Machine Intelligence, 13, 1115-1138, 1991.

↑ ページ冒頭 ← 前ページ