問題５−２−１ 解答

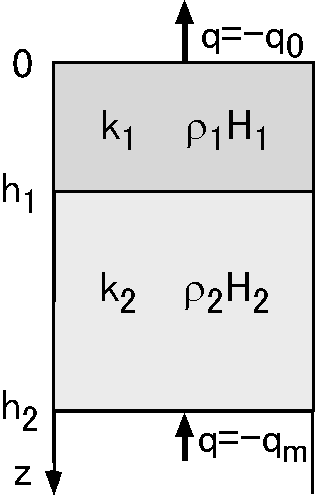
（１） 発熱源が一様分布で発熱量も一定の場合の熱伝導方程式は一般に， \begin{equation} \frac{d^2T}{dz^2} = -\frac{\rho H}{k}, \label{eq01} \end{equation} ですが，これを積分すると， \begin{equation} \frac{dT}{dz} = -\frac{\rho H}{k}z + C_1. \label{eq02} \end{equation} さらに積分して， \begin{equation} T = -\frac{\rho H}{2k}z^2 + C_1z + C_2, \label{eq03} \end{equation} となります．但し，\(C_1\) と \(C_2\) は積分定数です．よって，各層の熱流量 \(-k\frac{dT}{dz}\) と温度はこれらの積分定数をそれぞれの層の境界条件から決定することで得られます．

第１層（\(0\leq z\leq h_1\)）：

地表の熱流量が \(-q_0\) より，式 (2) から \[ \left[-k_1\frac{dT}{dz}\right]_{z=0} = -k_1C_1 = -q_0, \] より \(C_1=q_0/k_1\) となり， \(q\) は次式となります． \begin{equation} q = -k_1\frac{dT}{dz} = -q_0 + \rho_1H_1z. \label{eq04} \end{equation} 式 (3) で \(z=0\) で \(T=T_0\) より \(C_2=T_0\) となり次の温度の式を得ます． \begin{equation} T = T_0 + \frac{q_0}{k_1}z - \frac{\rho_1H_1}{2k_1}z^2. \label{eq05} \end{equation}

第２層（\(h_1\leq z\leq h_2\)）：

マントルからの熱流量が \(z=h_2\) で \(-q_m\) より，式 (2) から \[ \left[-k_2\frac{dT}{dz}\right]_{z=h_2} = \rho_2H_2h_2 - k_2C_1 = -q_m, \] より \(C_1 = (q_m+\rho_2H_2h_2)/k_2\) となり，次の \(q\) の式を得ます． \begin{equation} q = -k_2\frac{dT}{dz} = -q_m + \rho_2H_2(z - h_2). \label{eq06} \end{equation} 温度については， \(T\) が \(z=h_1\) で連続の条件から， \(C_2\) を決定します．式 (3) と式 (5) から， \[ -\frac{\rho_2 H_2}{2k_2}h_1^2 + \frac{q_m+\rho_2H_2h_2}{k_2}h_1 + C_2 = T_0 + \frac{q_0}{k_1}h_1 - \frac{\rho_1H_1}{2k_1}h_1^2, \] となり，整理すると次のようになります． \[ C_2 = T_0 + \left(\frac{q_0}{k_1}-\frac{q_m}{k_2}\right)h_1 - \frac{\rho_2H_2}{k_2}h_1h_2 + \left(\frac{\rho_2H_2}{k_2}-\frac{\rho_1H_1}{k_1}\right)\frac{h_1^2}{2}. \] よって，温度は式 (3) に \(C_1\) と \(C_2\) を代入して次式で表わされます． \begin{eqnarray} T & = & T_0 + \left(\frac{q_0}{k_1}-\frac{q_m}{k_2}\right)h_1 - \frac{\rho_2H_2}{k_2}h_1h_2 + \left(\frac{\rho_2H_2}{k_2}-\frac{\rho_1H_1}{k_1}\right)\frac{h_1^2}{2} \nonumber \\ & & + \frac{q_m + \rho_2H_2 h_2}{k_2}z - \frac{\rho_2H_2}{2k_2}z^2. \label{eq07} \end{eqnarray}

（２） この問題では \(q_m\) が既知で \(q_0\) を未知としています． \(q_0\) は \(z=h_1\) で熱流が連続であることから求めます．式 (4) と式 (6) から， \[ -q_0 + \rho_1H_1h_1 = -q_m + \rho_2H_2(h_1 - h_2), \] より， \begin{equation} q_0 = q_m + \rho_1H_1h_1 + \rho_2H_2(h_2 - h_1). \label{eq08} \end{equation} \(T_1\) は式 (5) に \(h_1\) を代入し， \(T_2\) は式 (7) に \(h_2\) を代入し整理すると次のようになります． \begin{eqnarray} T_1 & = & T_0 + \frac{q_0}{k_1}h_1 - \frac{\rho_1H_1}{2k_1}h_1^2, \label{eq09} \\ T_2 & = & T_0 + \frac{q_0}{k_1}h_1 + \frac{q_m}{k_2}(h_2-h_1) - \frac{\rho_1H_1}{2k_1}h_1^2 + \frac{\rho_2H_2}{2k_2}(h_2-h_1)^2. \label{eq10} \end{eqnarray}

\(h_1\) = 10 km， \(h_2\) = 40 km， \(k_1\) = \(k_2\) = 3 W/m K， \(\rho_1H_1\) = 2.5 μW/m³， \(\rho_2H_2\) = 0.5 μW/m³， \(q_m\) = 25 mW/m²， \(T_0\) = 0 °C とし，式 (8)〜(10) を計算すると， \[ q_0 = 65\ \mathrm{mW/m^2}, \quad T_1 = 175\ °\mathrm{C}, \quad T_2 = 500\ °\mathrm{C}. \]

問題５−２−２ 解答

球表面の熱流量 \(q_0\) は本文の式 (9) より， \[ q_0 = \frac{\rho Ha}{3}. \] 中心温度 \(T_C\) は本文の式 (8) より， \[ T_C = T_0 + \frac{\rho H}{6k}a^2. \] 上の \(q_0\) の式に地球の値を代入して単位体積当たりの発熱量 \(\rho H\) を求めると， \[ \rho H = 0.0375\ \mathrm{\mu W/m^3} \] と，マントルの推定値0.02 \(\mathrm{\mu W/m^3}\) より少し大きい程度となります．しかし，中心温度は， \[ T_C = 64000\ ^\circ\mathrm{C} \] と極端に大きな非現実的な値となります．これは地球内部の熱流や温度については熱伝導では説明できないことを示唆します．

問題５−２−３ 解答

（１） 熱伝導方程式， \[ \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dT}{dr}\right) = -\frac{\rho H_0}{k}\left(\frac{r}{a}\right)^n. \] を次のように変形し， \[ \frac{d}{dr}\left(r^2\frac{dT}{dr}\right) = -\frac{\rho H_0a^2}{k}\left(\frac{r}{a}\right)^{n+2} \] \(C_1\) と \(C_2\) を積分定数として積分します． \begin{align*} r^2\frac{dT}{dr} & = -\frac{\rho H_0a^3}{(n+3)k}\left(\frac{r}{a}\right)^{n+3} + C_1, \\ \frac{dT}{dr} & = -\frac{\rho H_0a}{(n+3)k}\left(\frac{r}{a}\right)^{n+1} + \frac{C_1}{r^2}, \\ T & =\! -\frac{\rho H_0a^2}{(n+2)(n+3)k}\!\left(\frac{r}{a}\right)^{n+2}\! -\! \frac{C_1}{r}\! +\! C_2. \end{align*} \(r\) = 0 で \(T\) が発散しない条件から \(C_1\) = 0．\(r=a\) で \(T=T_0\) より， \[ C_2 = T_0 + \frac{\rho H_0a^2}{(n+2)(n+3)k}. \] よって， \begin{align*} T & = T_0 + \frac{\rho H_0a^2}{(n+2)(n+3)k}\left(1 - \left(\frac{r}{a}\right)^{n+2}\right), \\ q & = \frac{\rho H_0a}{n+3}\left(\frac{r}{a}\right)^{n+1}. \end{align*}

（２） 表面の発熱量 \(\rho H_0\) と中心温度 \(T_C\) は， \[ \rho H_0 = \frac{(n+3)q_0}{a}, \quad T_C = T_0 + \frac{\rho H_0a^2}{(n+2)(n+3)k} \] となり，\(n\) = 2 と地球の値を代入すると， \[ \rho H_0 = 0.0625\ \mathrm{\mu W/m^3}, \quad T_C = 32000\ ^\circ\mathrm{C} \] となります．この発熱量はマントルの推定値0.02 \(\mathrm{\mu W/m^3}\) の 3 倍程度です．中心温度は発熱源が一様分布よりは低いですが，やはり非現実的な高温です．このモデルは，\(n\) が大きいほど発熱源の分布が球表面の近くに集中するので，試みに \(n\) = 20 で計算すると， \[ \rho H_0 = 0.2875\ \mathrm{\mu W/m^3}, \quad T_C = 5818\ ^\circ\mathrm{C} \] となり，発熱量は海洋地殻の平均値の推定値 0.5 \(\mu\)W/m³ より少し小さい程度で，中心温度も内核と外核の境界温度の推定値の約 6400°C (Bukowinski 1999) と符合します．しかし，球内部の温度分布は実際の地球とは全く異なります．例えば深さ 660 km の上部マントルと下部マントルの境界は約 2000°Cですが，このモデルでは 5000°C を超えてしまいます．問題5.2.2 と同様に，地球内部の熱の移動は熱伝導では説明できないことを示します．

参考文献：

• Bukowinski, M., Taking the core temperature, Nature, 401, 432-433, 1999.

→ ホーム