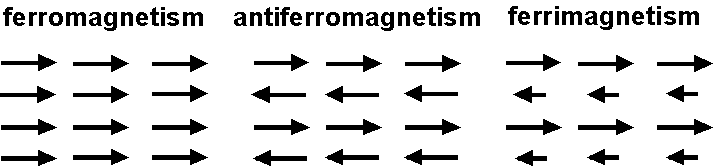
物質の磁性:強磁性(フェロ磁性)
強磁性は物質が磁性原子を含み,それらに強い相互作用がある場合に現れます.強磁性物質は原子の磁気モーメントの強い相互作用のために,磁場がなくても自発磁化(spontaneous magnetization)を示します.強磁性を示す元素は Fe, Ni, Co, Gd の4つだけですが,それらのいづれかの元素を含む多くの化合物も強磁性を示します.強磁性は ferromagnetism の和訳で,強い磁性についての一般的な用語です.しかし,厳密には ferromagnetism は下図のように原子の磁気モーメントの相互作用により生じる磁性の1つですので,以後フェロ磁性という用語を使用します.反強磁性(antiferromagnetism)は常磁性に似た弱い磁性ですが,磁化率は常磁性のそれよりも小さいです.それは反強磁性では,原子の磁気モーメントの強い相互作用のために熱擾乱の影響が小さいためです.フェリ磁性(ferrimagnetism)は基本的にはフェロ磁性と似ていますが,逆向きの磁気モーメントに異なる温度依存性があるときには,複雑な温度変化を示す場合があります.これらの磁性は全て,温度が臨界点のキューリー温度(Curie temperature) \(T_C\) を超えると常磁性となります.岩石の主要な磁性鉱物であるマグネタイト(magnetite) Fe3O4 はフェリ磁性です.
ワイスの理論
原子の磁気モーメントに働く強い相互作用は交換相互作用(exchange interaction)と呼ばれる量子力学でのみ説明される力が原因です.しかし,ワイスの理論(Weiss theory)を使えば基礎レベルの物理学の範囲でフェロ磁性の基本を理解できます.ワイスの理論では,相互作用は分子磁界(molecular field)とよばれる強い内部磁場 \({\bf H_m}\) が原因し,その磁場は物質の磁化 \({\bf M}\) に比例すると仮定します.即ち, \begin{equation} H_m = w M, \label{eq01} \end{equation} ここに, \(w\) は比例定数です.常磁性の理論で使用したと同じ統計力学を適用すると,ボルツマン因子は次のようになります. \[ \exp\left(\frac{\mu_0 m(H + wM)}{kT}\cos\theta\right). \] この係数を使用して, \(M\) は 常磁性と同じ方程式に異なる \(\alpha\) を代入した形で表すことができ, \begin{eqnarray} M & = &N m L(\alpha), \label{eq02} \\ \alpha & = & \frac{\mu_0 m(H + wM)}{kT}, \label{eq03} \end{eqnarray} となります.ここに, \(L(\alpha)\) はランジュバン関数です.ここで,自発磁化の温度変化を見るために \(H=0\) とします. (3) で \(H=0\) と置いて \(M\) は, \begin{equation} M = \frac{kT}{\mu_0 m w}\alpha. \label{eq04} \end{equation} となります. \(\alpha\) と \(M\) は \(T\) をパラメータとして方程式 (2) と (4) を解くことで決定できます.その解は下図のように, (2) (ランジュバン関数)の曲線と (4) の直線との交点となります. 温度 \(T\) が 0 K から高くなるにつれ,交点はランジュバン関数の曲線上を右上方から左下方へ移動します.臨界点のキューリー温度 \(T_C\) では交点は原点に到達します.キューリー温度を超えると,分子磁界 \(H_m\) 即ち \(wM\) は消失し,フェロ磁性は常磁性となります.
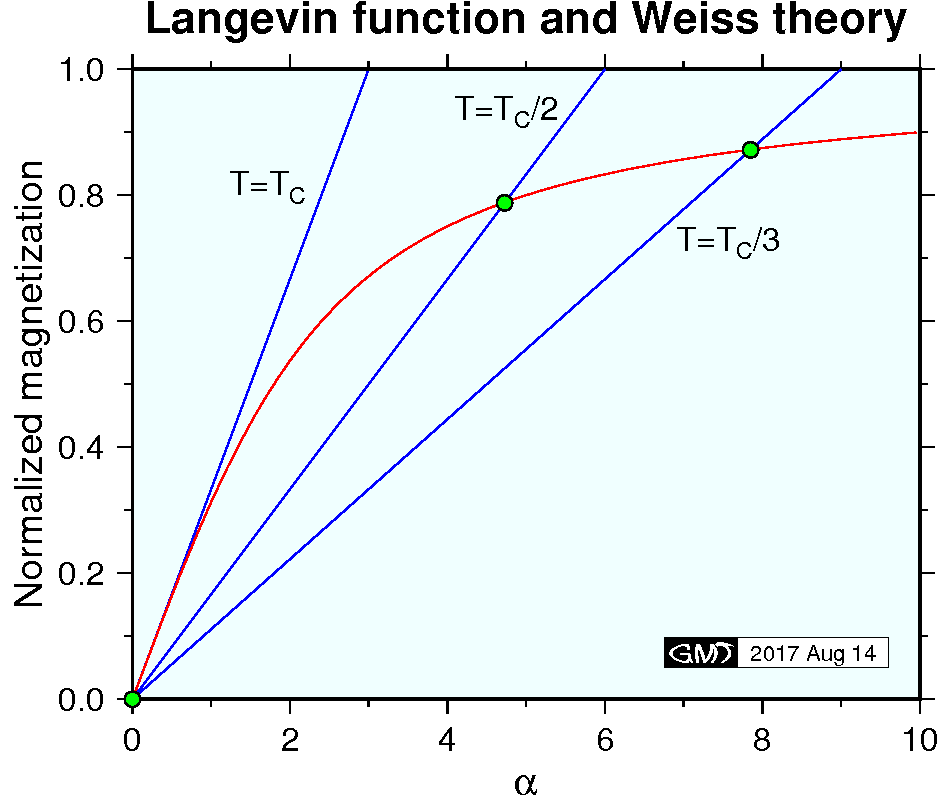
キューリー温度 \(T_C\) では, (2) と (4) の接線は等しくなります.小さな \(\alpha\) に対する近似式 \(L(\alpha) \sim \alpha/3\) を適用し, (2) と (4) の傾きが \(\alpha=0\) で等しいと置くと,次の関係が得られます. \[ \frac{N m}{3} = \frac{k T_C}{\mu_0 m w}. \quad (\alpha \ll 1) \] この式から定数 \(w\) は次のように表されます. \begin{equation} w = \frac{3 k T_C}{\mu_0 N m^2}. \label{eq05} \end{equation} (5) を (4) に代入すると \(M\) は, \begin{equation} M = \frac{N m}{3} \frac{T}{T_C} \alpha. \label{eq06} \end{equation} となります.規格化した変数 \(M^*=M/Nm\) と \(T^*=T/T_C\) を導入すると, (2) と (6) は次式で与えられます. \begin{eqnarray} M^* & = & L(\alpha) \label{eq07} \\ M^* & = & \frac{T^*}{3} \alpha \label{eq08} \end{eqnarray} これらの方程式の解析解はありませんが,標準的なルーチンを使用して数値計算で解を求めることは容易です(Press et al. 1992, 等).下図は数値計算で得られた \(M^*\)-\(T^*\) 曲線(赤線)です.また, Ni の常温より高い温度範囲での測定結果(青線)も載せています.
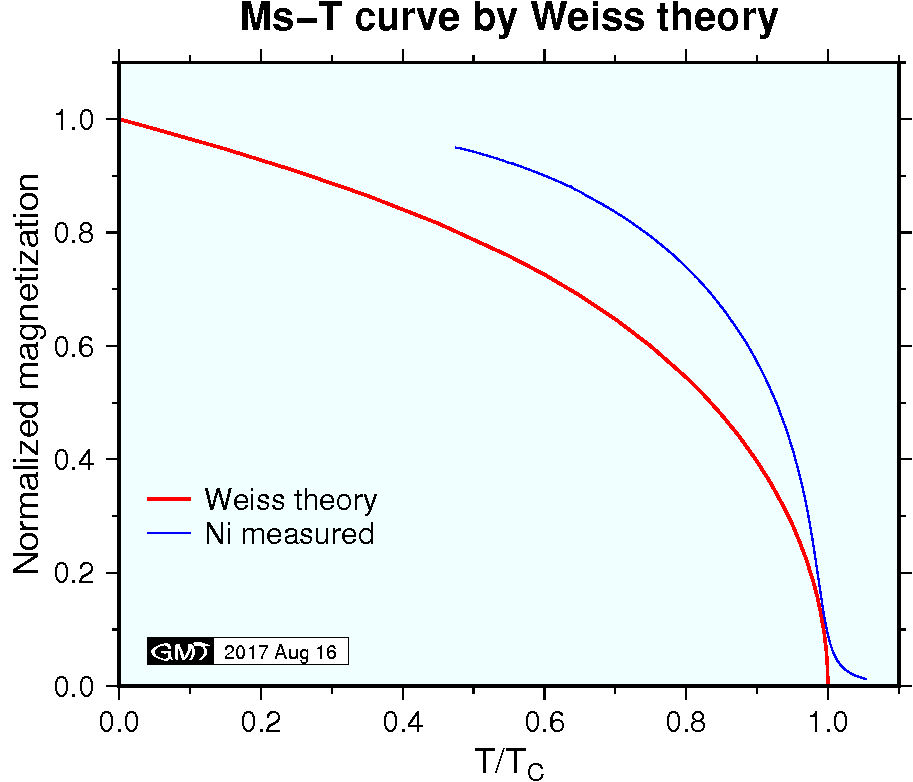
上図で, Ni の測定結果に低温のデータが無いことは別にして,理論と実験の曲線の不一致は小さくないです.ワイスの理論は量子力学を導入することで改善し,測定結果との一致も大変良くなります(近角, 1978).また,理論曲線は \(H\) = 0 として計算したのに対して, Ni のデータは \(B\) = 1 T の強磁場のもとで測定されたことには注意する必要があります.それ故, Ni の曲線には \(T_C\) より高い温度で常磁性の振る舞いが見られます.
キューリー温度 \(T_C\) が分かれば, \(w\) を (5) から計算し, \(H_m\) を (1) から見積もることができます.鉄の場合は, 分子量は 55.8 g で密度は 7.87 g/cm3 です.よって, \[ N = \frac{6.022\times10^{23}}{55.8/7.87} = 8.49\times10^{22}\ \mathrm{cm^{-3}} = 8.49\times 10^{28}\ \mathrm{m^{-3}}. \] \(T_C\) は 1044 K で \(m\) は 2.2 \(m_B\) (Fe イオンとは異なります)ですので, (5) を用いて \(w\) は, \[ w = \frac{3(1.3807\times10^{-23})(1044)} {(4\pi\times10^{-7})(8.49\times10^{28})(2.2\times9.273\times10^{-24})^2} = 974. \] となります.これらの値を用いて, (1) から \(H_m\) は次のように見積もれます. \[ H_m = wM = wNm = 974(8.49\times10^{28})(2.2\times9.273\times10^{-24}) = 1.69\times10^{9}\ \mathrm{A/m}. \] これは人工的に作り出すことが不可能な巨大な磁場(\(B\) = 2120 T)で,量子力学の交換相互作用のみで説明することができます.
参考文献:
- 近角聰信, 強磁性体の物理(上)--物質の磁性--, 299 pp., 裳華房, 東京, 1978.
- Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing (Second Edition), 994 pp., Cambridge University Press, Cambridge 1992.