物質の磁性：反磁性と常磁性

反磁性

反磁性の正確な記述には電子軌道のラーモア歳差運動（Larmor precession）の理論に基づく難解な物理学が必要ですので，ここでは入門的な説明を記します．反磁性は電子による環状の電流と外部磁場との電磁誘導によって生じます．外部磁場が新たに加えられると，その磁場を打ち消すように電流が変化し，外部磁場と逆向きの磁気モーメントが発生します．反磁性は全ての原子に備わる磁性ですが，より磁性の大きな常磁性が現れる原子ではそれにより隠されてしまいます．典型的な反磁性の物質は石英（quartz, SiO₂）です．石英はしばしば種々の磁気測定で試料ホルダーとして利用されます．そのため，サンプルの磁気が小さい場合には試料ホルダーによる負の磁気の影響について注意する必要があります．

常磁性

常磁性は，磁気モーメントを持つ原子を含むが，それらの間に相互作用が無いような物質に生じます．熱擾乱により原子の磁気モーメントはランダムな方向を向いており，そのため物質全体としては磁気モーメントはゼロとなります．磁場が加えられた場合は，原子の磁気モーメントは部分的に磁場方向に揃うことになります．

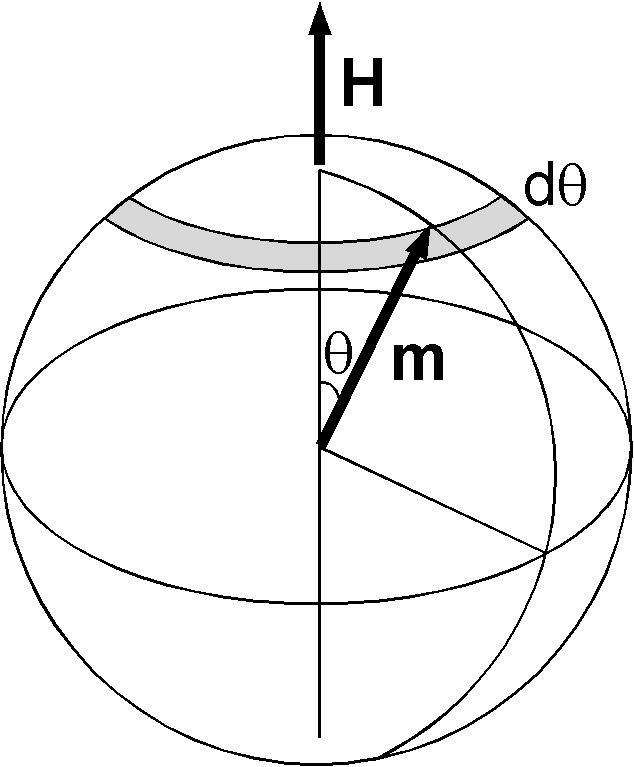
右図は原子の磁気モーメント \({\bf m}\) が，加えられた磁場 \({\bf H}\) から角度 \(\theta\) 傾いた状態を示します．この状態の磁気ポテンシャルエネルギー \(U\) は次式で表されます． \begin{equation} U = -\mu_0 m H \cos\theta. \label{eq01} \end{equation} 統計力学によると，温度 \(T\) K でのこの状態の発生確率は次のボルツマン因子（Boltzmann's factor）で与えられます． \begin{equation} \exp\left(-\frac{U}{kT}\right) = \exp\left(\frac{\mu_0mH}{kT}\cos\theta\right), \label{eq02} \end{equation} ここに， \(k\) = 1.3807×10^-23 J/K はボルツマン定数（Boltzmann's constant）です． 磁気モーメントが \(\theta\) と \(\theta+d\theta\) の間の方向を向く確率は次式で与えられます． \begin{equation} p(\theta)d\theta = \frac{2\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta} {2\pi \int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta}. \label{eq03} \end{equation} 磁場により誘起される物質の磁化 \({\bf M}\) は \({\bf m}\) の \({\bf H}\) 方向の成分により生じます．よって， \(M\) は， \[ M = N m \overline{\cos\theta}, \] となります．ここに， \(N\) は単位体積あたりの原子数です． (3) を使用して \(M\) は， \begin{eqnarray*} M & = & N m \int_0^\pi \cos\theta p(\theta) d\theta, \\ & = & N m \frac{\int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \cos\theta \sin\theta d\theta} {\int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta}. \end{eqnarray*} となります． \(\frac{\mu_0mH}{kT} = \alpha\) と \(\cos\theta = x\) を代入すると， \[ M = N m \frac{\int_{-1}^1 e^{\alpha x} x dx}{\int_{-1}^1 e^{\alpha x} dx}. \] 分母は次のように容易に求まります． \[ \int_{-1}^1 e^{\alpha x} dx = \frac{e^\alpha - e^{-\alpha}}{\alpha}. \] この結果を \(\alpha\) で微分すると分子は次のように求まります． \[ \int_{-1}^1 e^{\alpha x} x dx = \frac{e^\alpha + e^{-\alpha}}{\alpha} - \frac{e^\alpha - e^{-\alpha}}{\alpha^2}. \] それ故， \(M\) は， \begin{eqnarray} M & = & N m \left( \frac{e^\alpha + e^{-\alpha}}{e^\alpha - e^{-\alpha}} - \frac{1}{\alpha} \right) \nonumber \\ & = & N m L(\alpha) \label{eq04} \end{eqnarray} となります．ここに， \(L(\alpha)\) は次のランジュバン関数（Langevin function）です． \begin{equation} L(\alpha) = \left( \coth\alpha - \frac{1}{\alpha} \right). \label{eq05} \end{equation} 一般に \(\alpha\) は概して小さな値となります． 1 ボーア磁子に 1×10⁶ A/m (1.26 T の \(B\)) の非常に強い磁場が加えられた場合は， \[ \alpha = \frac{\mu_0m_BH}{kT} = \frac{(4\pi\times10^{-7})(9.274\times10^{-24})(1\times10^6)} {(1.3807\times10^{-23})(300)} = 0.0028. \] となります． \(\alpha \ll 1\) では，次の近似式が成立します． \begin{eqnarray*} \frac{e^\alpha + e^{-\alpha}}{e^\alpha - e^{-\alpha}} & = & \frac{1}{\alpha}\frac{1+\frac{1}{2}\alpha^2+\frac{1}{24}\alpha^4+\cdots} {1+\frac{1}{6}\alpha^2+\frac{1}{120}\alpha^4+\cdots} \\ & \approx & \frac{1}{\alpha}\left(1+\frac{1}{2}\alpha^2+\frac{1}{24}\alpha^4+\cdots\right) \left(1-\frac{1}{6}\alpha^2-\frac{1}{120}\alpha^4+\frac{1}{36}\alpha^4+\cdots\right) \\ & \approx & \frac{1}{\alpha}\left(1+\frac{1}{3}\alpha^2-\frac{1}{45}\alpha^4+\cdots\right). \end{eqnarray*} よって， \begin{equation} L(\alpha) \approx \frac{1}{3} \alpha \quad (\alpha \ll 1). \label{eq06} \end{equation} (6) を使用して， (4) の \(M\) は， \[ M = \frac{N m}{3} \alpha = \frac{\mu_0 N m^2 H}{3 k T}, \] となり，磁化率 \(\chi = M/H\) は次式で与えられます． \begin{equation} \chi = \frac{\mu_0 N m^2}{3kT}. \label{eq07} \end{equation} これは常磁性でのキューリーの法則（Curie's law） で， \(\chi\) が温度の逆数に比例することを表します．

常磁性の \(\chi\) を正確に導くには量子力学を導入する必要があるものの， (7) はかなり尤もな値を与えます．例として，イルメナイト（ilmenite, FeTiO₃）の磁化率を考えます．イルメナイトは極低温では反強磁性（次ページ参照）ですが， 300 K では常磁性です．イルメナイトの分子量は 151.7 g ですので， \[ N = 6.022\times10^{23}/151.7 = 3.970\times10^{21}\ \mathrm{g^{-1}} = 3.970\times10^{24}\ \mathrm{kg^{-1}}, \] となり， Fe²⁺ イオンの磁気モーメントを， \[ m = 5.4m_B = 5.4\times9.273\times10^{-24}\ \mathrm{Am^2}, \] とすれば， (7) から次の値を得ます． \[ \chi_{mass} = 101\times10^{-8}\ \mathrm{m^3/kg}. \] これは報告されている値， (100~113)×10^-8 m³/kg （Dunlop & Ozdemir, 1997）と良く一致しています．

参考文献：

• Dunlop, D. J., and O. Ozdemir, Rock Magnetism --- Fundamentals and frontiers ---, 573 pp., Cambridge University Press, Cambridge, 1997.

↑ ページ冒頭   ← 前ページ   → 次ページ