直線近似 y = a + bx: York (1966) の特別解
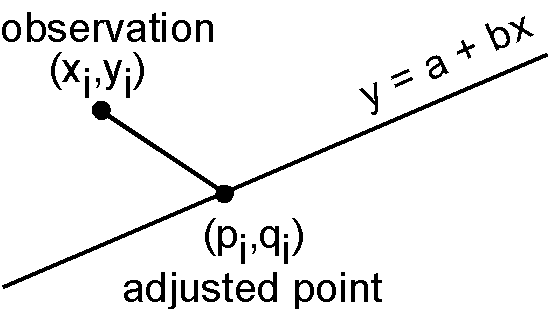古地磁気強度（古地球磁場強度）の実験における Arai plot の解析のために York (1966) の特別解を使用することが Coe et al. (1978) で提唱されました． York の理論では次の \(t\) を最小にします．
\[ t = \sum_{i=1}^n \{w(x_i)(x_i - p_i)^2 + w(y_i)(y_i - q_i)^2\}, \]
ここに \(w(x_i)\) と \(w(y_i)\) は観測値の重みです．理論は非常に複雑な \(b\) の一般的方程式を展開しますがここでは示しません．より簡単ないくつかの特別解のうち，
\[ \frac{w(x_i)}{w(y_i)} = c \quad (\mathsf{constant}) \]
と仮定したときの方程式は，
\[
\left( \sum_{i=1}^n w(x_i) u_i v_i \right)b^2
- \left( \sum_{i=1}^n w(x_i) v_i^2 - c\sum_{i=1}^n w(x_i) u_i^2 \right)b
- c\sum_{i=1}^n w(x_i) u_i v_i = 0,
\]
で与えられます．但し， \(u_i\) と \(v_i\) は次のとおりです．
\[ u_i = x_i - \bar x, \quad v_i = y_i - \bar y. \]
この特別方程式には３つのケースがあり， Coe et al. (1978) は次の条件で与えられる最後のケースを採用することを提唱しました．
\[
w(x_i) = \frac{1}{\sigma_x^2} = \frac{n-1}{\sum_{i=1}^n u_i^2}, \quad
w(y_i) = \frac{1}{\sigma_y^2} = \frac{n-1}{\sum_{i=1}^n v_i^2}.
\]
すると， \(b\) は次の簡単な式で与えられます．
\begin{equation}
b = \sqrt{ \frac{\sum_{i=1}^n v_i^2}{\sum_{i=1}^n u_i^2} } = \frac{\sigma_y}{\sigma_x}. \label{eq01}
\end{equation}
York (1966) はまた次の \(b\) の標準誤差と呼ばれる \(\sigma_b\) の推定値も導いています．
\begin{equation}
\sigma_b^2 = \frac{1}{n-2}\frac{2\sum_{i=1}^n v_i^2 - 2b\sum_{i=1}^n u_i v_i}{\sum_{i=1}^n u_i^2}, \label{eq02}
\end{equation}
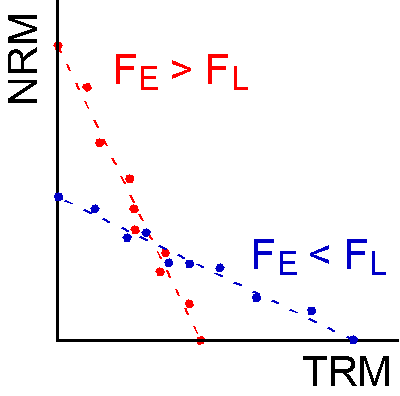
上の重み \(w(x_i)\) と \(w(y_i)\) に適用した \(\sigma_x^2\) と \(\sigma_y^2\) は必ずしも \(x_i\) と \(y_i\) の誤差を反映するものではありません．というのは，それらは平均の周りの分散だからです．しかし，それらは Arai plot における誤差に対する一般的認識と合います．即ち，測定誤差の絶対値は残留磁化強度に比例するというものです．その場合，図から分かるように \(x_i\) と \(y_i\) の誤差は次式で表されます． \[ \sigma_{x_i}^2 = (F_L \sigma)^2, \quad \sigma_{y_i}^2 = (F_E \sigma)^2, \] ここに \(F_L\) と \(F_E\) はそれぞれ実験室磁場と古地磁気の強度で， \(\sigma\) は一般的測定誤差を反映する定数です．よって，上の \eqref{eq01} と \eqref{eq02} で与えられる \(b\) と \(\sigma_b\) は正しいと考えられます．
参考文献:
- Coe, R. S., S. Gromme, and E. A. Mankinen, Geomagnetic paleointensities from radiocarbon-dated lava flows on Hawaii and the question of the Pacific nondipole low,J. Geophys. Res., 83, 1740-1756, 1978.
- York, D., Least-squars fitting of a straight line,Can. J. Phys., 44, 1079-1086, 1966.