直線近似 y = a + bx: yとxの両方が誤差を含む
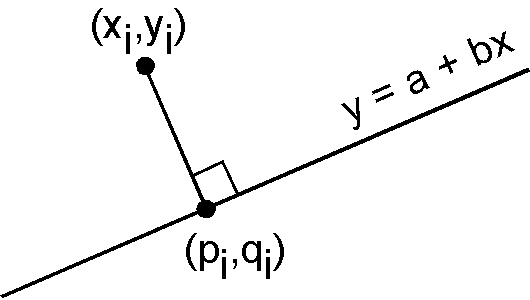次の \(t\) を最小にします．
\[ t = \sum_{i=1}^n \{(x_i - p_i)^2 + (y_i - q_i)^2\}. \]
容易に分かるように \(t\) は次式で表されます．
\[ t = \frac{1}{b^2 + 1} \sum_{i=1}^n (y_i - a - bx_i)^2. \]
\(\partial t/\partial a = 0\) から \(a = \bar y - b\bar x\) を得ます．但し， \(\bar x = \sum_{i=1}^n x_i/n\)， \(\bar y = \sum_{i=1}^n y_i/n\) です．よって， \(t\) は
\begin{eqnarray*}
t & = & \frac{1}{b^2+1}\sum_{i=1}^n \{(y_i - \bar y) - b(x_i - \bar x)\}^2, \\
& = & \frac{1}{b^2+1}\sum_{i=1}^n (v_i - bu_i)^2,
\end{eqnarray*}
となります．ここに， \(u_i = x_i - \bar x\)， \(v_i = y_i - \bar y\) です． \(\partial t/\partial b = 0\) とし， \(S_{uu} = \sum_{i=1}^n u_i^2\)， \(S_{vv} = \sum_{i=1}^n v_i^2\)， \(S_{uv} = \sum_{i=1}^n u_i v_i\) と置けば次式が得られます．
\[ S_{uv}b^2 - (S_{vv} - S_{uu})b - S_{uv} = 0. \]
この方程式を解くことで， \(b\) が次のように得られます．
\begin{equation}
b = \frac{(S_{vv} - S_{uu}) \pm \sqrt{(S_{vv} - S_{uu})^2 + 4S_{uv}^2}}{2S_{uv}}. \label{eq01}
\end{equation}
しかし，古地磁気強度（古地球磁場強度）の研究における Arai plot の解析には通常この方法や前ページで示した方法は使用しません．代わって，次頁に示すように York (1966) の特別解を使用します．