偏心双極子: Hurwitz (1960) の公式
地磁気は通常,地心双極子磁場に高次の非双極子磁場を加えて表現されます.これは数学上の扱いとして便利だからで,地磁気を1つの偏心双極子として表すことも可能です.地磁気の正確な表現のためには,地心双極子のずれにより生じるガウス係数を,低次の項だけではなく高次の項まで決定することが望ましいです.いかなる次数のガウス係数も求めることが可能な公式が Hurwitz (1960) により提出されました. Hurwitz の論文は記述が簡潔なため,数学を得意としない者にはその理論を理解することは困難です.以下の易しい解説は佐納(2000)に基づいてます.
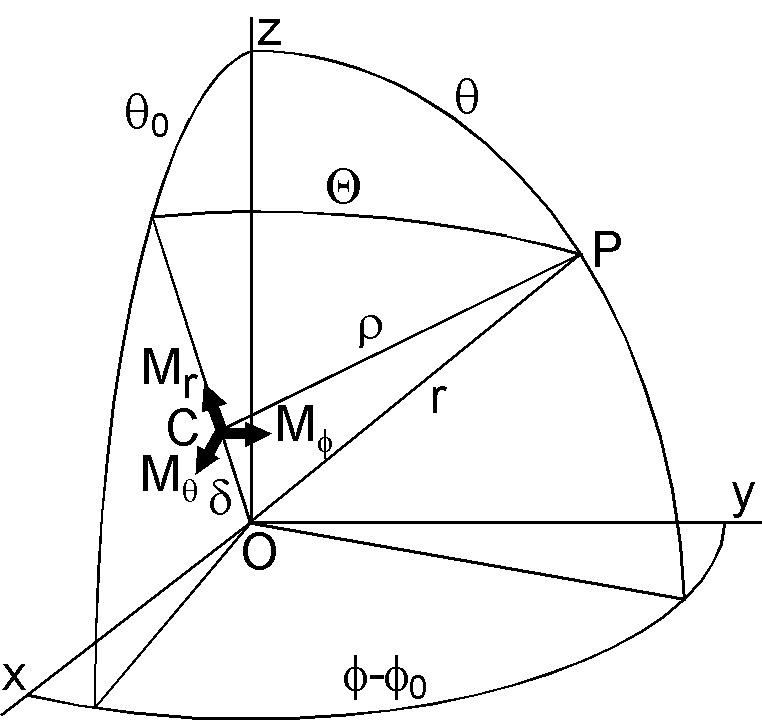
地球の中心 O に位置する双極子を \({\bf M}=(M_x,M_y,M_z)\) とします.いま,この双極子をその向きは保ったまま点 C \((x_c,y_c,z_c)\) へずらします.ずれ \(\overrightarrow{\mathsf{OC}}\) を表すベクトル \(\boldsymbol{\delta}=(x_c,y_c,z_c)\) を導入し,極座標系では \((\delta,\theta_0,\phi_0)\) とします.また,観測点を P \((r,\theta,\phi,)\), \(\overrightarrow{\mathsf{CP}}\) をベクトル \(\boldsymbol{\rho}\), 角度 \(\angle\mathsf{COP}\) を \(\Theta\) とします.
偏心双極子の直交座標系における成分は \((M_x,M_y,M_z)\) で,偏心双極子がどこに位置しようと同じです.しかし,球座標系における成分 \((M_r,M_\theta,M_\phi)\) は \(\boldsymbol{\delta}\) に依存します.各座標系での成分は座標系の回転行列によって次のような関係にあります. \begin{equation} \left(\begin{array}{c} M_\theta \\ M_\phi \\ M_r \end{array}\right) = \left(\begin{array}{ccc} \cos\phi_0\cos\theta_0 & \sin\phi_0\cos\theta_0 & -\sin\theta_0 \\ \label{eq01} -\sin\phi_0 & \cos\phi_0 & 0 \\ \cos\phi_0\sin\theta_0 & \sin\phi_0\sin\theta_0 & \cos\theta_0 \end{array}\right) \left(\begin{array}{c} M_x \\ M_y \\ M_z \end{array}\right) \end{equation}
そこで,点 P におけるポテンシャル \(W\) を3つのポテンシャルの和として表します. \begin{equation} W = W_r + W_\theta + W_\phi, \label{eq02} \end{equation} ここで, \(W_r\), \(W_\theta\), \(W_\phi\) はそれぞれ \({\bf M_r}\), \({\bf M}_\boldsymbol{\theta}\), \({\bf M}_\boldsymbol{\phi}\) によるポテンシャルです.ポテンシャル \(W_r\) は次式で与えられます. \[ W_r = \frac{\mu_0}{4\pi}\frac{{\bf M_r}\cdot\boldsymbol{\rho}}{\rho^3} = \frac{\mu_0}{4\pi}\frac{{\bf M_r}\cdot({\bf r} - \boldsymbol{\delta})}{\rho^3} = \frac{\mu_0}{4\pi}\frac{M_r r\cos\Theta -M_r\delta}{\rho^3}. \] 次の \(\cos\Theta\) に関する式, \begin{equation} \cos\Theta = \cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0), \label{eq03} \end{equation} を利用して, \(W_r\) は次式のようになります. \begin{equation} W_r = \frac{\mu_0}{4\pi}\frac{M_r r\left(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - \frac{\delta}{r}\right)}{\rho^3}. \label{eq04} \end{equation} \(W_\theta\) については, \({\bf M}_\boldsymbol{\theta}\) と \({\bf r}\) とのなす角度を \(\Theta'\) とすると, \(\cos\Theta'\) は \eqref{eq03} で \(\theta_0\) を \(\theta_0+\pi/2\) で置き換えれば良いことを利用します.よって, \(W_\theta\) は次式となります. \begin{equation} W_\theta = \frac{\mu_0}{4\pi}\frac{M_\theta r\left(-\cos\theta\sin\theta_0 + \sin\theta\cos\theta_0\cos(\phi-\phi_0)\right)}{\rho^3}. \label{eq05} \end{equation} 同様にして, \(W_\phi\) は次式で与えられます. \begin{equation} W_\phi = \frac{\mu_0}{4\pi}\frac{M_\phi r\sin\theta\sin(\phi-\phi_0)}{\rho^3}. \label{eq06} \end{equation}
次に, \(r\) で規格化された2つの距離の変数を導入します; \begin{equation} \xi = \frac{\rho}{r}, \qquad h = \frac{\delta}{r}. \label{eq07} \end{equation} すると,3つのポテンシャルは以下の式で与えられることは容易に分かります. \begin{eqnarray} W_r & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\left(\frac{1}{\xi}\right), \label{eq08} \\ W_\theta & = & \frac{\mu_0}{4\pi}\frac{M_\theta}{r^2}\frac{1}{h}\frac{\partial}{\partial\theta_0}\left(\frac{1}{\xi}\right), \label{eq09} \\ W_\phi & = & \frac{\mu_0}{4\pi}\frac{M_\phi}{r^2}\frac{1}{h\sin\theta_0}\frac{\partial}{\partial\phi_0}\left(\frac{1}{\xi}\right). \label{eq10} \end{eqnarray} 式 \eqref{eq08} を確認するために, \eqref{eq07} の定義を用いて, \(\xi\) を以下のように変形します. \begin{eqnarray*} \xi & = & \rho/r = \left.\sqrt{r^2 - 2r\delta\cos\Theta + \delta^2}\right/r, \\ & = & \sqrt{1 - 2h(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0)) + h^2}. \end{eqnarray*} そして, \(1/\xi\) を \(h\) で偏微分すると, \begin{eqnarray*} \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\left(\frac{1}{\xi}\right) & = & -\frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{1}{\xi^2}\frac{\partial \xi}{\partial h} \\ & = &\frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - h}{\xi^3} \\ & = & \frac{\mu_0}{4\pi}\frac{M_r r\left(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - \frac{\delta}{r}\right)}{\rho^3}, \end{eqnarray*} を得ますが,これは式 \eqref{eq04} そのものです.同様にして, \eqref{eq09} と \eqref{eq05},及び \eqref{eq10} と \eqref{eq06} が同一であることが確認されます.
最後に,ルジャンドル陪関数に関する2つの式を使います.1つは次の母関数です. \[ \frac{1}{\xi} = \frac{1}{\sqrt{1 - 2\cos\Theta h + h^2}} = \sum_{n=0}^\infty P_n(\cos\Theta)h^n. \] 他の1つは次の加法定理です. \begin{eqnarray*} P_n(\cos\Theta) & = & P_n(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0)), \\ & = & \sum_{m=0}^n P_n^m(\cos\theta)P_n^m(\cos\theta_0)\cos m(\phi-\phi_0). \end{eqnarray*} これらの式を \eqref{eq08} に代入すると, \(W_r\) は以下のように変形されます. \begin{eqnarray*} W_r & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\sum_{n=0}^\infty\sum_{m=0}^n P_n^m(\cos\theta)P_n^m(\cos\theta_0)\cos m(\phi-\phi_0) h^n, \\ & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{\delta}{r}\right)^{n-1}n P_n^m(\cos\theta_0) \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta), \\ & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_r}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}n P_n^m(\cos\theta_0) \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta). \end{eqnarray*} よって, \(W_r\) から生じるガウス係数は次式で与えられます. \begin{equation} {g_r}_n^m = \frac{\mu_0 M_r}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}n P_n^m(\cos\theta_0)\cos m\phi_0, \quad {h_r}_n^m = {g_r}_n^m \tan m\phi_0. \label{eq11} \end{equation} 同様に, \eqref{eq09} の \(W_\theta\) は, \begin{eqnarray*} W_\theta & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_\theta}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{d P_n^m(\cos\theta_0)}{d\theta_0} \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta), \end{eqnarray*} となるので \(W_\theta\) によるガウス係数は次式で与えられます. \begin{equation} {g_\theta}_n^m = \frac{\mu_0 M_\theta}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{d P_n^m(\cos\theta_0)}{d\theta_0}\cos m\phi_0, \quad {h_\theta}_n^m = {g_\theta}_n^m \tan m\phi_0. \label{eq12} \end{equation} 式 \eqref{eq10} の \(W_\phi\) も, \begin{eqnarray*} W_\phi & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_\phi}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{m}{\sin\theta_0} P_n^m(\cos\theta_0) \\ & & \times(-\sin m\phi_0 \cos m\phi + \cos m\phi_0 \sin m\phi)P_n^m(\cos\theta), \end{eqnarray*} と表され, \(W_\phi\) によるガウス係数は次式となります. \begin{eqnarray} {g_\phi}_n^m & = & -\frac{\mu_0 M_\phi}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{m}{\sin\theta_0} P_n^m(\cos\theta_0)\sin m\phi_0, \label{eq13} \\ {h_\phi}_n^m & = & -{g_\phi}_n^m \cot m\phi_0. \nonumber \end{eqnarray}
まとめとしては,点 C \((x_c,y_c,z_c)\),即ち \((\delta,\theta_0,\phi_0)\),に位置する偏心双極子 \({\bf M}=(M_x,M_y,M_z)\) に起因するガウス係数を求める手順は次の通りです.まず最初に,式 \eqref{eq01} を用いて \({\bf M}\) を \((M_\theta,M_\phi,M_r)\) に変換します.そして, \(W_r\), \(W_\theta\), \(W_\phi\) に対するガウス係数を,それぞれ \eqref{eq11}, \eqref{eq12}, \eqref{eq13} を用いて計算します.最後に全体のガウス係数は次式で与えられます. \[ g_n^m = {g_r}_n^m + {g_\theta}_n^m + {g_\phi}_n^m, \quad h_n^m = {h_r}_n^m + {h_\theta}_n^m + {h_\phi}_n^m. \]
References:
- Hurwitz, L., Eccentric dipoles and spherical harmonic analysis, J. Geophys. Res., 65, 2555-2556, 1960.
- 佐納康治, 私信, 朝日大学, 2000.