■このページでは数式を表示するのに MathJaxを使っています。一部のブラウザで表示されない、または表示が乱れる可能性があります。他のブラウザで試してみてください。(Google Chrome推奨)
目次
- 第1章
- 運動方程式を解いてみよう(1次元の運動)
- (1-1)
- 一定の力が働く物体の運動を考えてみよう
- (1-2)
- 水ロケットカー(水を噴出して進む車)の原理とその運動方程式
- (1-3)
- 圧力タンク型水ロケットカーの原理とその運動方程式
- (1-4)
- 空気ロケットカー(圧縮空気を噴出する勢いで進む車)の原理とその運動方程式
- 第2章
- ロケットの軌道計算にチャレンジ(2次元の運動)
- (2-1)
- 初速度を与えられたロケットの運動(放物運動)
- (2-2)
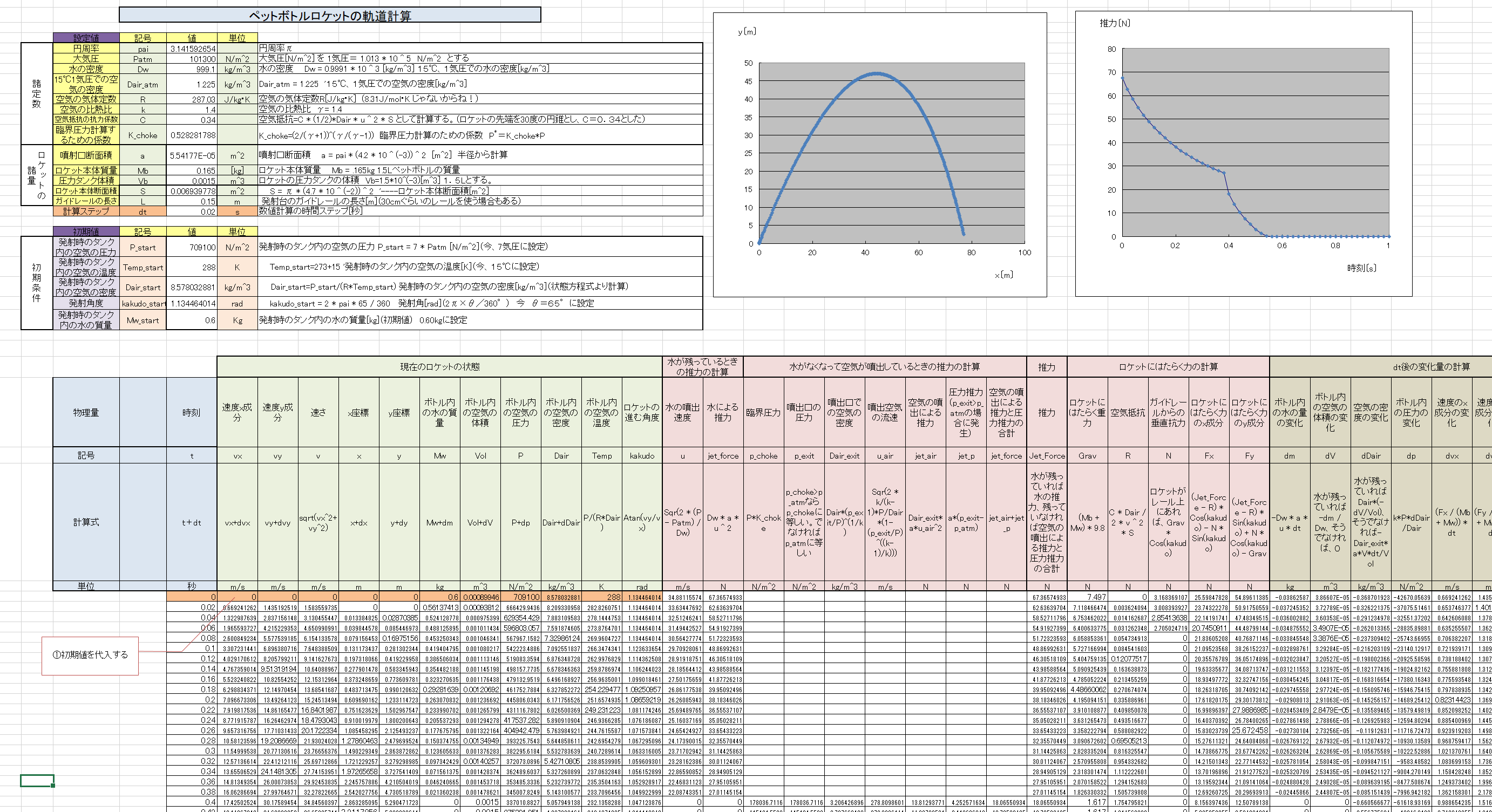
- ペットボトルロケットの軌道計算
- 第3章
- 参考文献
第1章 運動方程式を解いてみよう(1次元の運動)
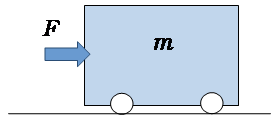
(1-1)一定の力が働く物体の運動を考えてみよう
図のように、質量\(m\)の物体に、一定の力\(F\)の力を加えた場合を考えよう。物体の運動方程式は
 \begin{equation}
ma=F
\end{equation}
となる。加速度\(a\)は、\(\frac{F}{m}\)となり、
\begin{equation}
ma=F
\end{equation}
となる。加速度\(a\)は、\(\frac{F}{m}\)となり、
時刻\(t\)での速度\(v\)および、位置\(x\)は、
\begin{align}
v=v_{0}+\frac{F}{m}t, x=x_0+v_{0}t+\frac{1}{2}\frac{F}{m}t^2
\end{align}
となることがわかっている。この運動は、等加速度直線運動と呼ばれている運動である。
ここで、\(v_0\)、\(x_0\)は、時刻0での速度、位置を表している。
これ以降の問題では全て\(v_0=0\)、\(x_0=0\)として計算することにする。
加速度\(a\)は、\(\frac{dv}{dt}\)と表すことができる。(1)式を書き直すと、
\begin{equation}
m\frac{dv}{dt}=F
\end{equation}
となる。このような式を微分方程式という。ここでは、このような微分方程式を数値計算で解いていこう。
\(\frac{dv}{dt} \fallingdotseq \frac{\varDelta v}{\varDelta t}\)として、この式を変形してみると、
\begin{align}
\varDelta v=\frac{F}{m} \varDelta t
\end{align}
今、時刻\(t\)での速度を\(v(t)\)、位置を\(x(t)\)として、
時刻\(\varDelta t\)後の速度\(v(t+\varDelta t)\)、および
位置\(x(t+\varDelta t)\)を求めるには、
\begin{align}
v(t+\varDelta t) =v(t) +F/m・\varDelta t
\end{align}
\begin{align}
x(t+\varDelta t) =x(t) +v(t)・\varDelta t
\end{align}
とする。このようにして、少しずつ時間を進めて、速度、位置を求めていく。
これはオイラー法と呼ばれる方法である。
つまり、物体の運動方程式をたてることができれば、物体の運動を調べる(速度と位置を調べる)ことができる。
それでは、エクセルを使って数値計算することで、この運動方程式を解いてみよう。
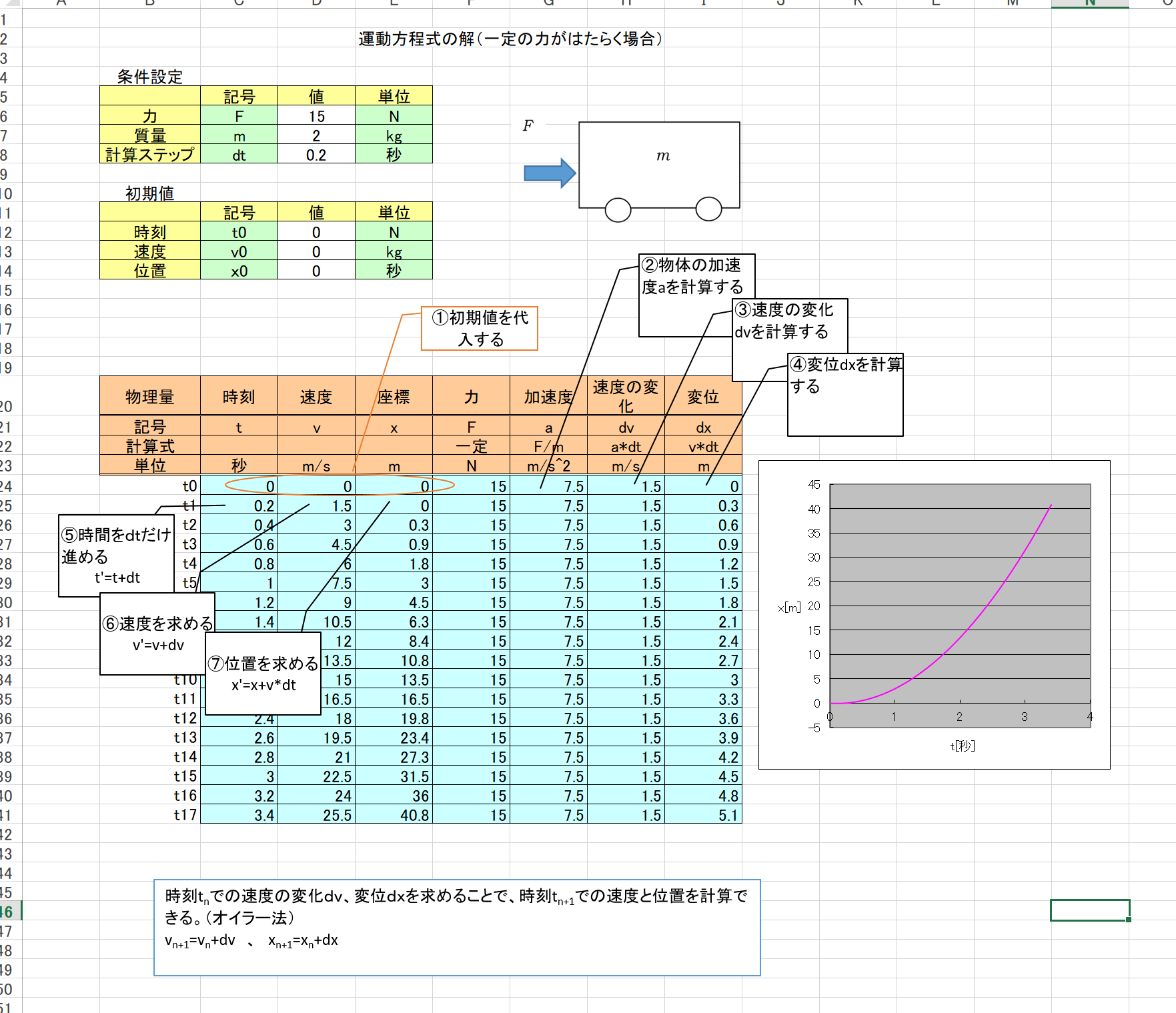
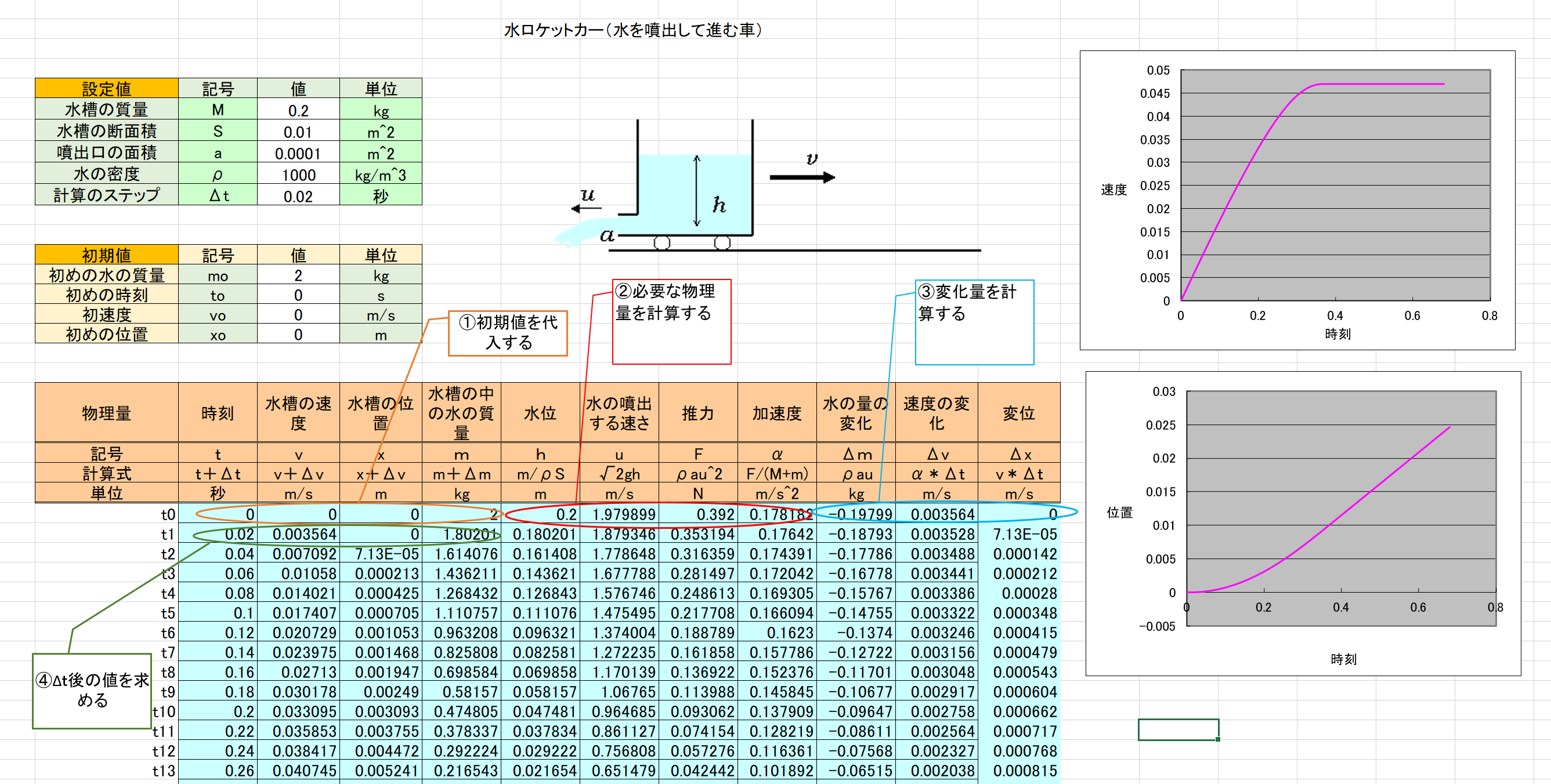
(1-2)水ロケットカー(水を噴出して進む車)の原理とその運動方程式
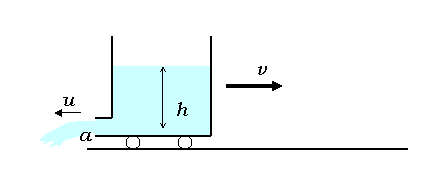
図のように、水槽(水タンク)の底に小さな穴があり、水を噴出しながら進む台車(水ロケットカー)を考えてみよう。
水を噴出するとき、台車(水ロケットカー)は図右向きに力を受ける。この力を推力と呼ぶ。
この水ロケットカーの推力を求めてみよう。
今、水ロケットカーの質量(中に入っている水の質量を含むロケットカー全体の質量)が\(m\)とする。
このロケットカーが毎秒、質量\(\beta\)の水を、ロケットカーに対して、\(u\)の速さで噴出しているとする。
微小な時間\(\varDelta t\)間に、ロケットカーの速さが\(v\) から\(v+\varDelta v\)に変化したとする。
地面に対するの水の速度を\(w\) とすれば、相対速度の関係式より、\(-u=w-v\)であり、\(w=v-u\)となり、また
ロケットカーが噴出する水の質量は\(\beta\cdot\varDelta t\)なので、運動量保存の法則より、
\begin{align}
mv=( m-\beta\varDelta t)(v+\varDelta v)+ \beta\varDelta t\cdot w
\end{align}
すなわち、
\begin{align}
mv=( m-\beta\varDelta t)(v+\varDelta v)+\beta\varDelta t\cdot (v-u)
\end{align}
ここで\(\varDelta t×\varDelta v\)の項は無視して整理すると、
\begin{align}
m\frac{\varDelta v}{\varDelta t}=\beta u
\end{align}
となる(文献5)。
微分方程式の形で書けば、
\begin{align}
m\frac{dv}{dt}=\beta u
\end{align}
となる。これは、ロケットの運動方程式を表している。ということは、
右辺はロケットカーにはたらく力なので、これはすなわち推力を表している。
さて、水が噴出している穴(噴出口)の面積を\(a\)、水の密度を\(\rho_w\)とすると、
\begin{align}
\beta=\rho_w a u
\end{align}
と表されるので、(10)式を書き換えると、
\begin{align}
m\frac{dv}{dt}=\rho_w a u^2
\end{align}
また、この式の中の\(m\)は、時間とともに変化することに注意しよう。この\(m\)の変化は、水が出て行った分だけ減少するので、
\begin{align}
\frac{dm}{dt}=-\beta
\end{align}
\begin{align}
\frac{dm}{dt}=-\rho_w a u
\end{align}
と書くことができる。
また、これまで、噴出する水の速さを\(u\)としてきたが、
これは、水タンクの中の水の水位(噴出口から水面の高さ)を\(h\)として、噴出口が十分小さい場合には、ベルヌーイの定理より、
\begin{align}
u=\sqrt{2gh}
\end{align}
となることがわかっている。(参考文献 6および8)
また、この\(h\)は、水が噴出するとともに減少する。
単位時間に、水は\(au\)だけ外に出るので、水タンクの断面積を\(A\)として、
\begin{align}
\frac{dh}{dt}=-\frac{1}{A} au
\end{align}
と表される。
ここまで、時間とともに変化する物理量として、\(v,u,m,h\)が出てきた。
式(12)、(14)、(15)、(16)をまとめてみると、
\begin{eqnarray}
\left\{
\begin{array}{llll}
m\frac{dv}{dt}=\rho_w a u^2\\
\frac{dm}{dt}=-\rho_w a u\\
\frac{dh}{dt}=-\frac{1}{A}au\\
ここで、\\
u=\sqrt{2gh}
\end{array}
\right.
\end{eqnarray}
これらの式は、連立の微分方程式の形をしているが、これらを解けば、この物体の運動を調べることができる。
前述したオイラー法の考え方がわかっていれば、数値計算の方法は難しくない。
それでは、エクセルを使ってこの微分方程式を解いてみよう。
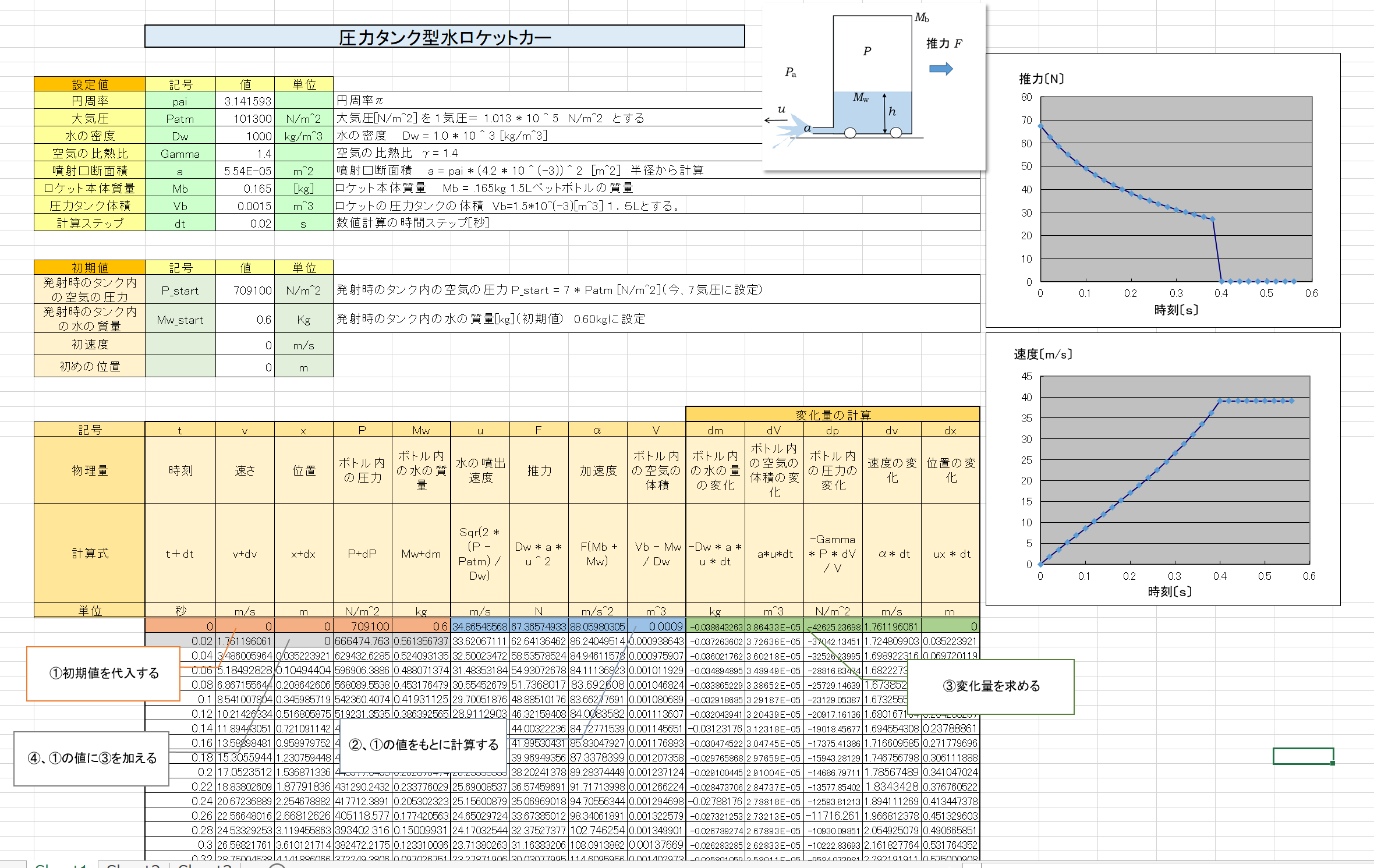
(1-3)圧力タンク型水ロケットカーの原理とその運動方程式
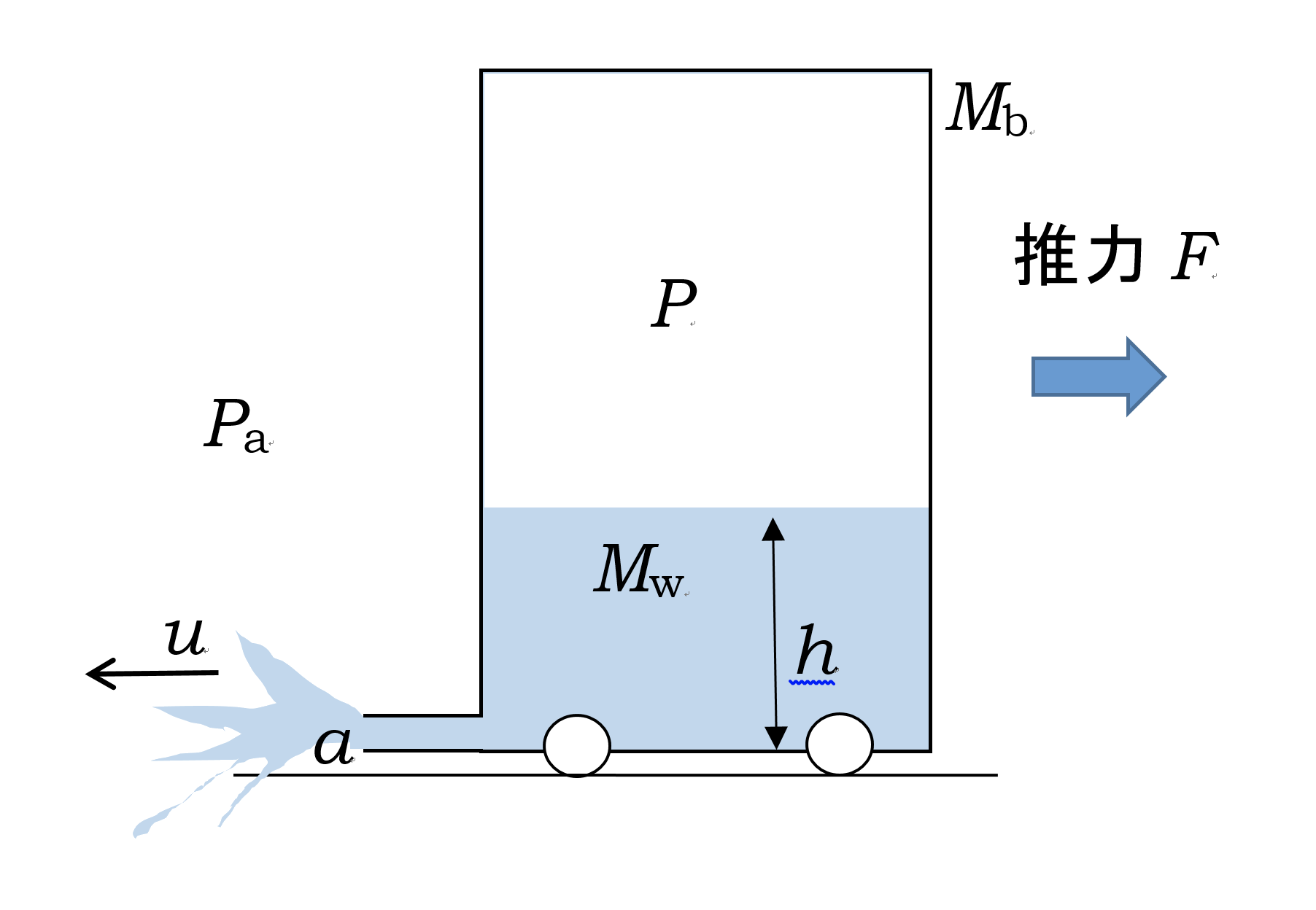 図のように、密閉型のタンクに水を入れ、中に圧縮空気を入れた台車(圧力タンク型水ロケットカー)を考えよう。
水が圧力タンク内の圧力により噴出し、その推力によって台車は進む。ここでは、水が全部出てしまう前までの運動を考えてみる。水が出終わってまだ圧縮空気が残っていれば、空気が噴出することでさらにロケットカーは加速されるが、空気の噴出による運動は、次の節(1−4)を参照してほしい。
図のように、密閉型のタンクに水を入れ、中に圧縮空気を入れた台車(圧力タンク型水ロケットカー)を考えよう。
水が圧力タンク内の圧力により噴出し、その推力によって台車は進む。ここでは、水が全部出てしまう前までの運動を考えてみる。水が出終わってまだ圧縮空気が残っていれば、空気が噴出することでさらにロケットカーは加速されるが、空気の噴出による運動は、次の節(1−4)を参照してほしい。
水(密度\(\rho_w\))が、断面積\(a\) の噴出口から、ロケットカーに対し速さ \(u\) で噴出するとき、
推力\(F\)は、(9)式の右辺と同様に
\begin{align}
F=\beta u =\rho_w au^2
\end{align}
となる。よって、運動方程式は、(10)式と同様に、
\begin{align}
m\frac{dv}{dt}=\rho_w a u^2
\end{align}
と表される。ここで水ロケットカーの質量(中に入っている水の質量を含むロケットカー全体の質量)を\(m\)とする。
この\(m\)の変化は、水が出て行った分だけ減少するので、式(14)と同様に、
\begin{align}
\frac{dm}{dt}=-\rho_w a u
\end{align}
さて、ここで水が噴出する速さ\(u\)はどのような式で表されるか考えてみよう。
圧力タンク内の圧力を\(P\)、タンクの断面積を\(A\)、タンク内の水の流速を\(U\)、
また、噴射口の断面積を\(a\)、 噴射口での水の流速を\(u\)、そして大気圧を\(P_a\)とすると、
流体力学の基礎式であるベルヌーイの式および連続の式より、
\begin{align}
\frac{1}{2}\rho_w U^2 + P +\rho_w g h=\frac{1}{2}\rho_w u^2 + P_a
\end{align}
\begin{align}
U\cdot A=u\cdot a
\end{align}
がなりたつ。ここで\(g\)は重力加速度、\(h\)は噴射口から水面までの高さである。この2式から、
\begin{align}
u=\frac{1}{\sqrt{1-(a/A)^2}}\sqrt{2(P-P_a)/\rho_w +2gh}
\end{align}
となる(文献7)。
これを式(18)に代入すれば推力は
\begin{align}
F=\frac{2a}{1-(a/A)^2}(P-P_a+\rho_w gh)
\end{align}
となる。
ちなみに、噴出口が十分小さく、
また、中に入れた圧縮空気が大気圧より十分大きく、
\(A \gg a , (P-P_a)\gg \rho_w gh \)が成り立っているとすれば、
近似的には、
\begin{align}
u=\sqrt{2(P-P_a)/\rho_w }
\end{align}
\begin{align}
F=2a(P- P_a)
\end{align}
としても大きな違いはない。後述する数値計算では、この近似を使うことにする。
圧力タンク内の圧力\(P\)は水の噴出に伴い急激に減少するが、この変化は断熱変化とみなし計算してみよう。
今、圧力タンクの中の空気の体積を\(V\)、圧力を\(P\)とし、微小な時間\(dt\)後、それぞれ、\(V+dV\)、\(P+dp\) と変化したとすると、断熱変化の関係式より
\begin{align}
PV^\gamma=(P+dp)(V+dV)^\gamma
\end{align}
ここで、\(\gamma\)は、空気の比熱比である。
この式を変形すると、
\begin{align}
PV^\gamma=PV^\gamma(1+\frac{dp}{P})(1+\frac{dV}{V})^\gamma
\end{align}
さらに、
\begin{align}
(1+\frac{dV}{V})^\gamma \fallingdotseq 1+\gamma \frac{dV}{V}
\end{align}
の近似式を用い、また、\(\frac{dP}{P} \times \frac{dV}{V} \)の項を無視して整理すると、
\begin{align}
\frac{dP}{P}=-\gamma \frac{dV}{V}
\end{align}
圧力タンクの圧縮空気の体積は、水が外に噴出した分だけ増加するので、
\begin{align}
dV=au\cdot dt
\end{align}
となる。これを代入して
\begin{align}
\frac{dP}{dt}=-\frac{\gamma P}{V} au
\end{align}
これで、計算の準備ができた。時間とともに変化する物理量として、\(v,u,m,P,V\)が出てきた。
式(19)、(20)、(25)、(31)、(32)をまとめてみると、
\begin{eqnarray}
\left\{
\begin{array}{llll}
m\frac{dv}{dt}=\rho_w a u^2\\
\frac{dm}{dt}=-\rho_w a u\\
\frac{dP}{dt}=-\frac{\gamma P}{V}au\\
\frac{dV}{dt}=au\\
ここで、\\
u=\sqrt{2(P-P_a)/\rho_w }
\end{array}
\right.
\end{eqnarray}
これらの連立の微分方程式を解けば、この物体の運動を調べることができる。 それでは、エクセルを使ってこの微分方程式を解いてみよう。
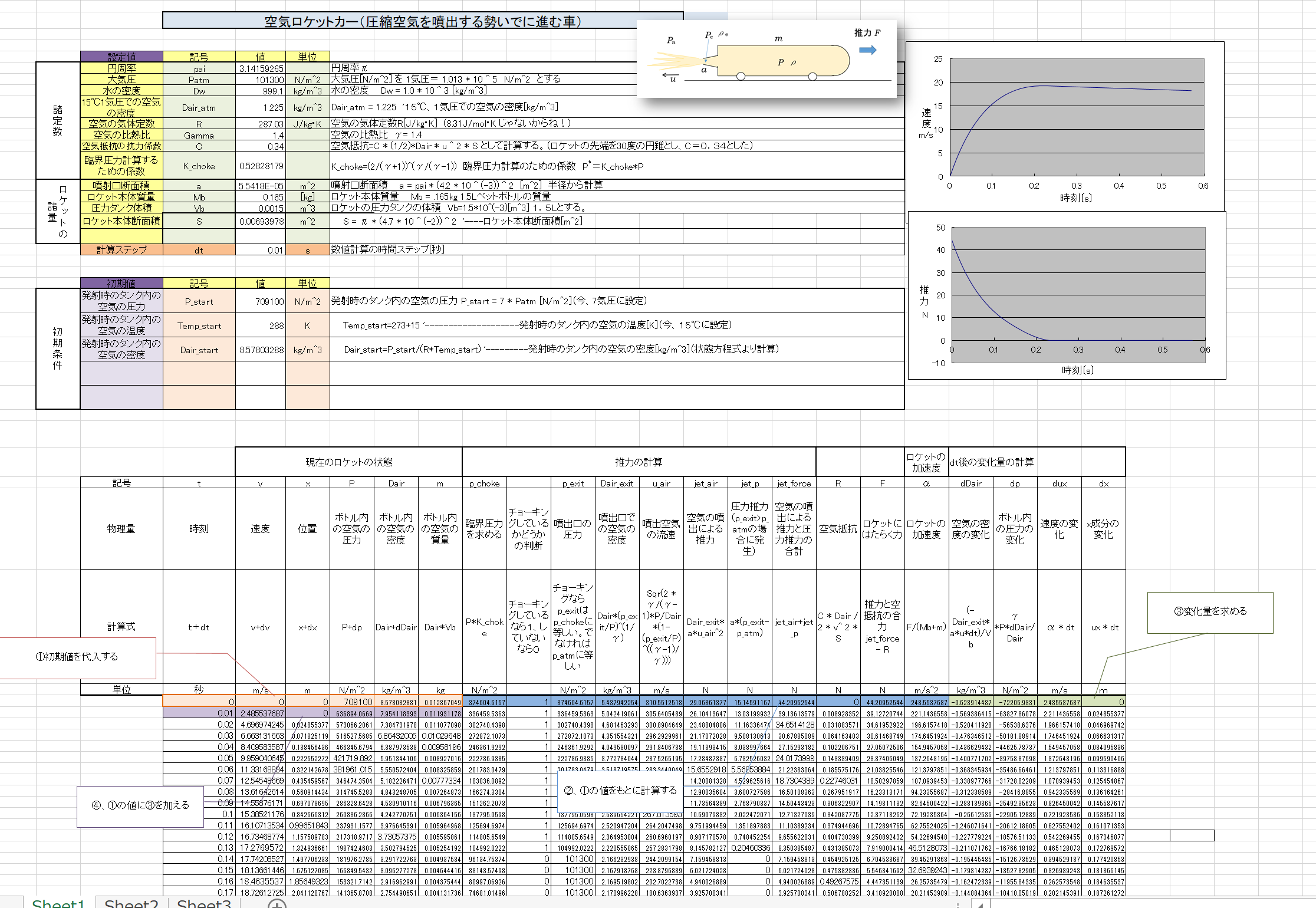
(1-4)空気ロケットカー(圧縮空気を噴出する勢いで進む車)の原理とその運動方程式
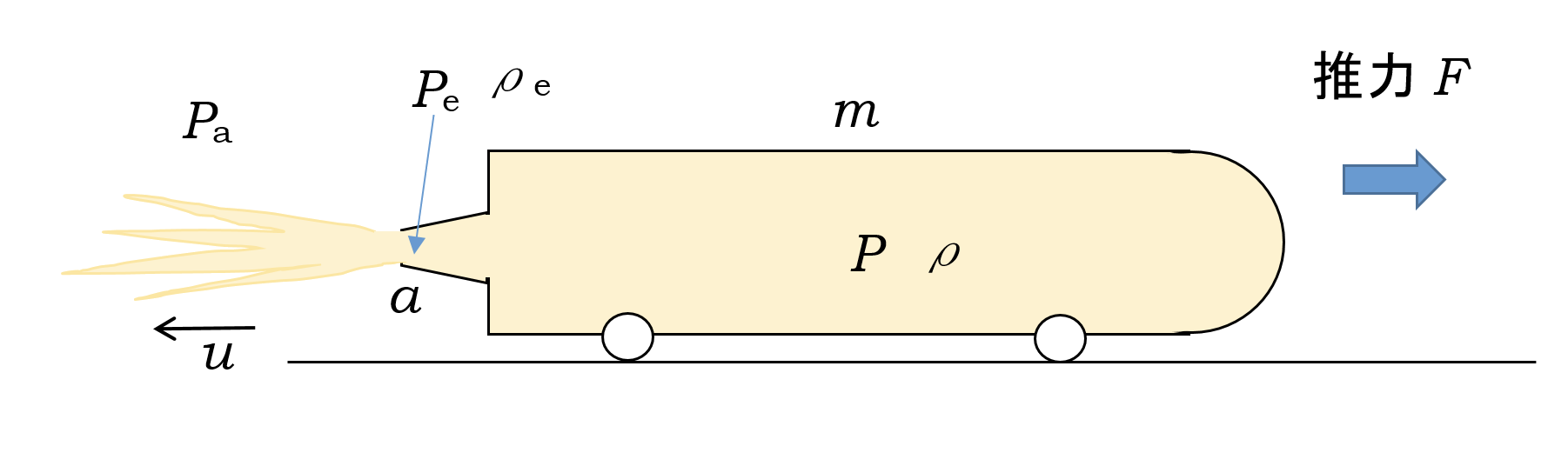
図のように、体積\(V_0\)の密閉型のタンクに圧縮空気を入れた台車(空気ロケットカー)を考えよう。
空気が圧力タンク内の圧力により、ノズルから噴出し、その推力によって台車は進む。
圧力タンク内の空気の圧力、空気の密度をそれぞれ、\(P,\rho \)、噴出口での値をそれぞれ、\(P_e,\rho_e \)、外部の大気圧を\(P_a\)とする。
断面積\(a\) の噴出口から、ロケットカーに対し速さ \(u\) で空気が噴出するとき、
運動方程式は、(19)式と同様に、
\begin{align}
m\frac{dv}{dt}=\rho_e a u^2
\end{align}
と表される。ここで空気ロケットカーの質量(中に入っている空気の質量を含むロケットカー全体の質量)を\(m\)とする。
また、式(20)と同様に、
\begin{align}
\frac{dm}{dt}=-\rho_e a u
\end{align}
さて、ここで空気が噴出する速さ\(u\)はどのような式で表されるか考えてみよう。これは、圧縮性流体についての流体力学の理論により、次式で表される。(文献8)
\begin{align}
u=\sqrt{\frac{2\gamma}{\gamma-1}\frac{P}{\rho}\left\{1-\left(\frac{P_e}{P}\right)^{\left(\gamma-1\right)/\gamma}\right\}}
\end{align}
ここで、\(\gamma\)は比熱比である。この式にでてくる\(P_e\)は、外気圧\(P_a\)とは必ずしも同じではないことに注意が必要である。内外の圧力差が大きいほど、単位時間あたりの噴出量が大きくなりそうに思われるが、実際には内部の圧力がある値より大きい時は、気体の噴出は、流れの閉塞(チョーキング)を起こし、\(P_e\)は外気圧まで下がることはない。
その状態では、噴出口での圧力\(P_e\)は、臨界圧力\(P^*\)となる(文献8)。この値は次式で表される。
\begin{align}
P^*=\left(\frac{2}{\gamma+1}\right)^\frac{\gamma}{\gamma-1}P
\end{align}
空気の比熱比\(\gamma=1.4\)を代入して計算すると、
\begin{align}
P^*=0.528P
\end{align}
となる。
例を上げて説明しょう。
今タンク内の圧力\(P\)が3気圧、外気圧\(P_a\)が1気圧だとしよう。臨界圧力を計算してみると、
\begin{align}
P^*=0.528 \times 3=1.58気圧
\end{align}
となる。この値は、外気圧の1気圧より大きいので、流れは閉塞状態になっている。
この時の噴出口の圧力\(P_e\)は
\begin{align}
P_e=P^*=1.58気圧
\end{align}
となり、外気の1気圧まで下がらない。
この値を(36)式に代入することで、\(u\)を求めることができる。
では、今タンク内の圧力\(P\)が1.8気圧まで下がったとしよう。臨界圧力は、
\begin{align}
P^*=0.528 \times 1.8=0.95気圧
\end{align}
となる。この値は、外気圧の1気圧より小さいので、流れは閉塞状態ではない。
この状態では、噴出口の圧力\(P_e\)は外気圧に等しく、
\begin{align}
P_e=P_a=1気圧
\end{align}
となる。この値を(36)式に代入して、\(u\)を求める。
さて、(34)式の右辺の推力は、運動量推力と呼ばれるが、噴出口での圧力\(P_e\)が外気圧\(P_a\)まで下がらないとき(つまり閉塞状態のとき)、圧力差による推力\(a(P_e - P_a)\)がこれに加わる(文献5)。
よって、(34)式の運動方程式は、次のように書き換えられる。
\begin{align}
m\frac{dv}{dt}=\rho_e a u^2+a(P_e - P_a)
\end{align}
( 例えば、https://www.grc.nasa.gov/www/k-12/airplane/rockth.html 又は、https://www.astronomicalreturns.com/p/section-33-rocket-thrust-equation.html を参照 )
次に、噴出口での気体の密度\(\rho_e\)の計算の仕方を考えよう。
これは、断熱変化の式
\begin{align}
\frac{P}{\rho^\gamma}=\frac{P_e}{\rho_e^\gamma}
\end{align}
より、
\begin{align}
\rho_e=\rho \left(\frac{P_e}{P}\right)^\frac{1}{\gamma}
\end{align}
として求めることができる。
最後に、気体が噴出するにつれてタンク内部の圧力\(P\)がどのように変化するか、考えてみよう。
式(35)より、時間\(dt\)間にタンクから外へ出る気体の質量\(dm\)は
\begin{align}
dm=-\rho_e a u\cdot dt
\end{align}
よって、タンク内の密度の変化は、タンクの体積を\(V_0\)として、
\begin{align}
d\rho=\frac{dm}{V_0}=\frac{-\rho_e a u}{V_0}\cdot dt
\end{align}
断熱変化の式より、
\begin{align}
\frac{P}{\rho^\gamma}=\frac{P+dp}{(\rho+d\rho)^\gamma}
\end{align}
これを整理して、
\begin{align}
1+\frac{dP}{P}=\left(1+\frac{d\rho}{\rho}\right)^\gamma
\end{align}
さらに、近似して、
\begin{align}
\frac{dP}{P}=\gamma \frac{d\rho}{\rho}
\end{align}
式(47)を代入して整理すると、
\begin{align}
\frac{dP}{dt}=-\gamma \frac{\rho_e P}{\rho V_0}au
\end{align}
これで、計算の準備ができた。時間とともに変化する物理量として、\(v,u,m,P,\rho_e,\rho\)が出てきた。
式(43)、(35)、(36)、(45)、(47)、(51)をまとめてみると、
\begin{eqnarray}
\left\{
\begin{array}{llll}
m\frac{dv}{dt}=\rho_e a u^2+a(P_e - P_a)\\
\frac{dm}{dt}=-\rho_e a u\\
\frac{d\rho}{dt}=\frac{-\rho_e a u}{V_0}\\
\frac{dP}{dt}=-\gamma \frac{\rho_e P}{\rho V_0}au\\
ここで、\\
u=\sqrt{\frac{2\gamma}{\gamma-1}\frac{P}{\rho}\left\{1-\left(\frac{P_e}{P}
\right)^{\left(\gamma-1\right)/\gamma}\right\}}\\
\rho_e=\rho \left(\frac{P_e}{P}\right)^\frac{1}{\gamma}
\end{array}
\right.
\end{eqnarray}
この式で、\(P_e\)の値については、まず臨界圧力
\(P^*=0.528P\)
を計算し、
\begin{eqnarray}
\left\{
\begin{array}{llll}
P^*\geqq P_aであれば、P_e=P^* (閉塞状態)\\
P^* < P_aであれば、P_e=P_a (閉塞状態ではない)\\
\end{array}
\right.
\end{eqnarray}
と代入する。
それでは、エクセルを使ってこの微分方程式を解いてみよう。このエクセルの数値計算では空気抵抗の影響を考慮している。これについては第2章の中で触れるのでそれを参照してほしい。
第2章 ロケットの軌道計算にチャレンジ(2次元の運動)
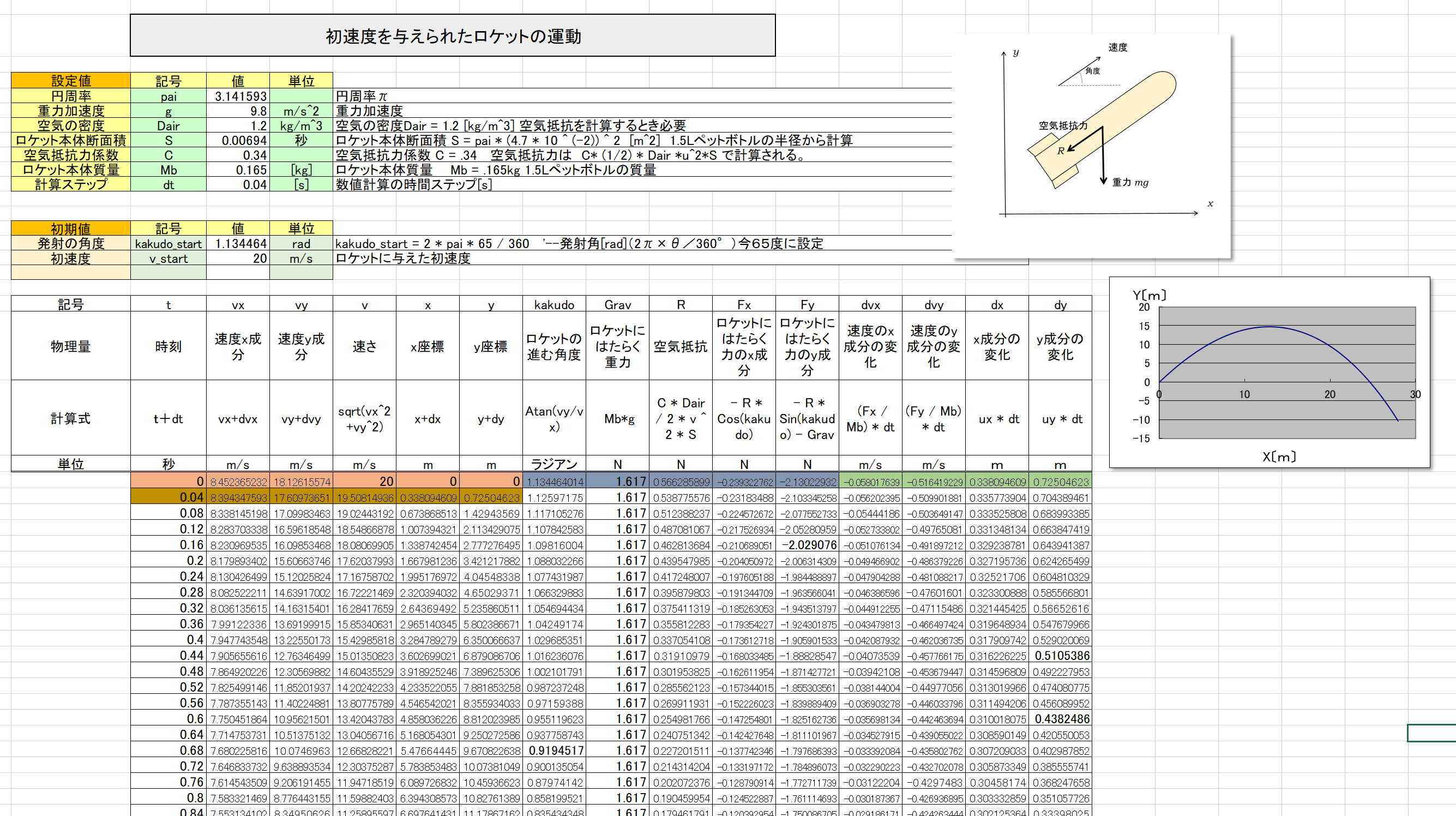
(2ー1)初速度を与えられたロケットの運動(放物運動)
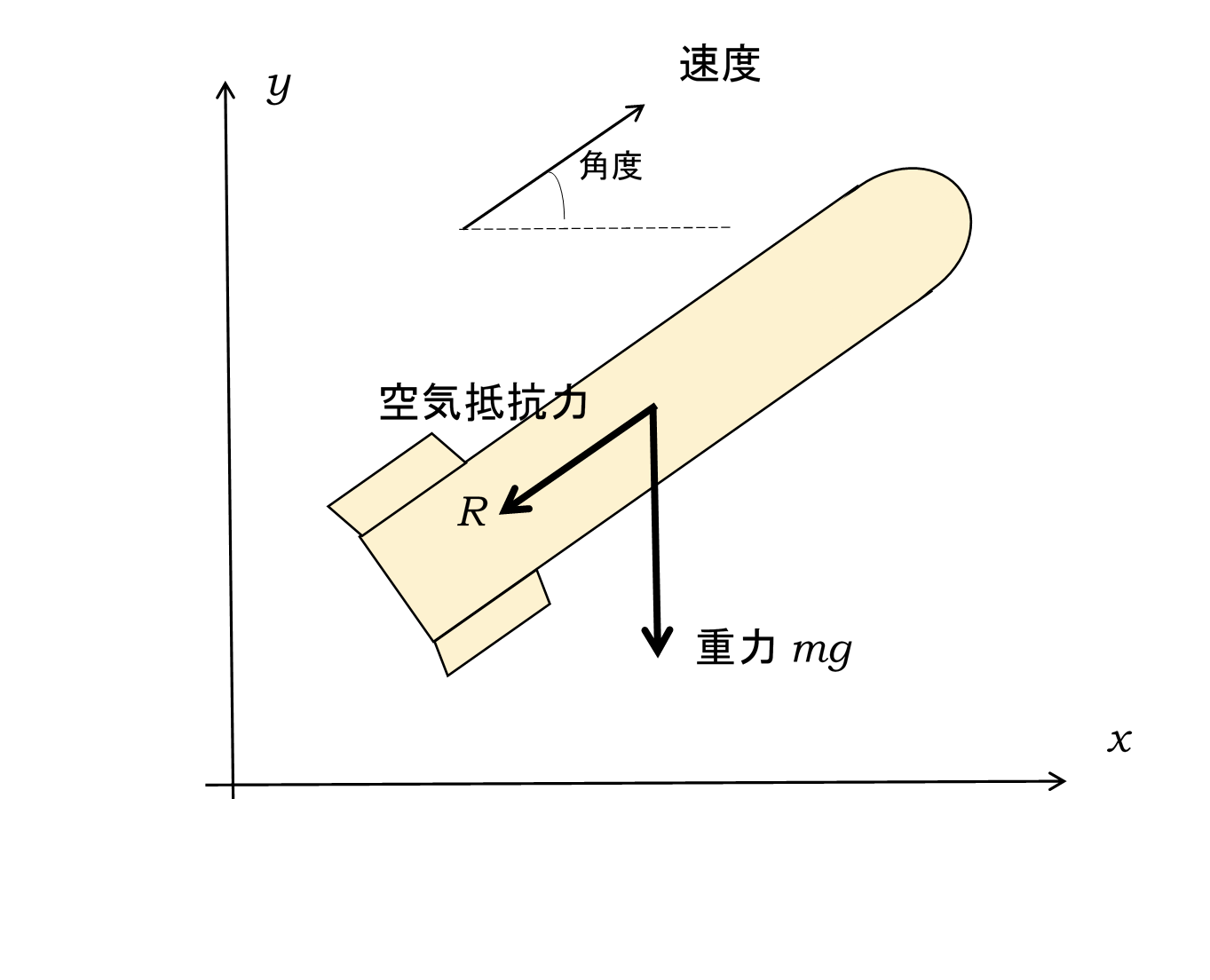 図のように、初速度を与えられたロケットの運動を考えてみよう。
図のように、水平方向をx軸、鉛直方向をy軸とし、それぞれに運動方程式をたてると、
\begin{equation}
m\frac{dv_x}{dt}=-R\cos\theta
\end{equation}
\begin{equation}
m\frac{dv_y}{dt}=-R\sin\theta-mg
\end{equation}
ここで、\(\theta\)は、ロケットの進行方向とx軸のなす角度であり、\(R\)は空気抵抗を表している。
ここで、空気抵抗\(R\)の式は、
\begin{equation}
R={1 \over 2}\rho v^{2}SC_D
\end{equation}
となる。
ここで\(\rho\) は空気の密度、\(v\) は物体の速さ( \(v=\sqrt{v_x^2+v_y^2}) \)、\(S\) は物体の代表面積(ここでは、ペットボトルの断面積)、\(C_D\) は抗力係数である。抗力係数は、物体の形状に依存する。たとえば、頂角30度の円錐の形であれば\(C_D=0.34\)となる(文献6)。
図のように、初速度を与えられたロケットの運動を考えてみよう。
図のように、水平方向をx軸、鉛直方向をy軸とし、それぞれに運動方程式をたてると、
\begin{equation}
m\frac{dv_x}{dt}=-R\cos\theta
\end{equation}
\begin{equation}
m\frac{dv_y}{dt}=-R\sin\theta-mg
\end{equation}
ここで、\(\theta\)は、ロケットの進行方向とx軸のなす角度であり、\(R\)は空気抵抗を表している。
ここで、空気抵抗\(R\)の式は、
\begin{equation}
R={1 \over 2}\rho v^{2}SC_D
\end{equation}
となる。
ここで\(\rho\) は空気の密度、\(v\) は物体の速さ( \(v=\sqrt{v_x^2+v_y^2}) \)、\(S\) は物体の代表面積(ここでは、ペットボトルの断面積)、\(C_D\) は抗力係数である。抗力係数は、物体の形状に依存する。たとえば、頂角30度の円錐の形であれば\(C_D=0.34\)となる(文献6)。
それでは、エクセルで解いてみよう。この計算では、ロケットの位置\( (x,y) \)をもとめ、軌道をグラフで表してみよう。
(2ー2)ペットボトルロケットの軌道計算
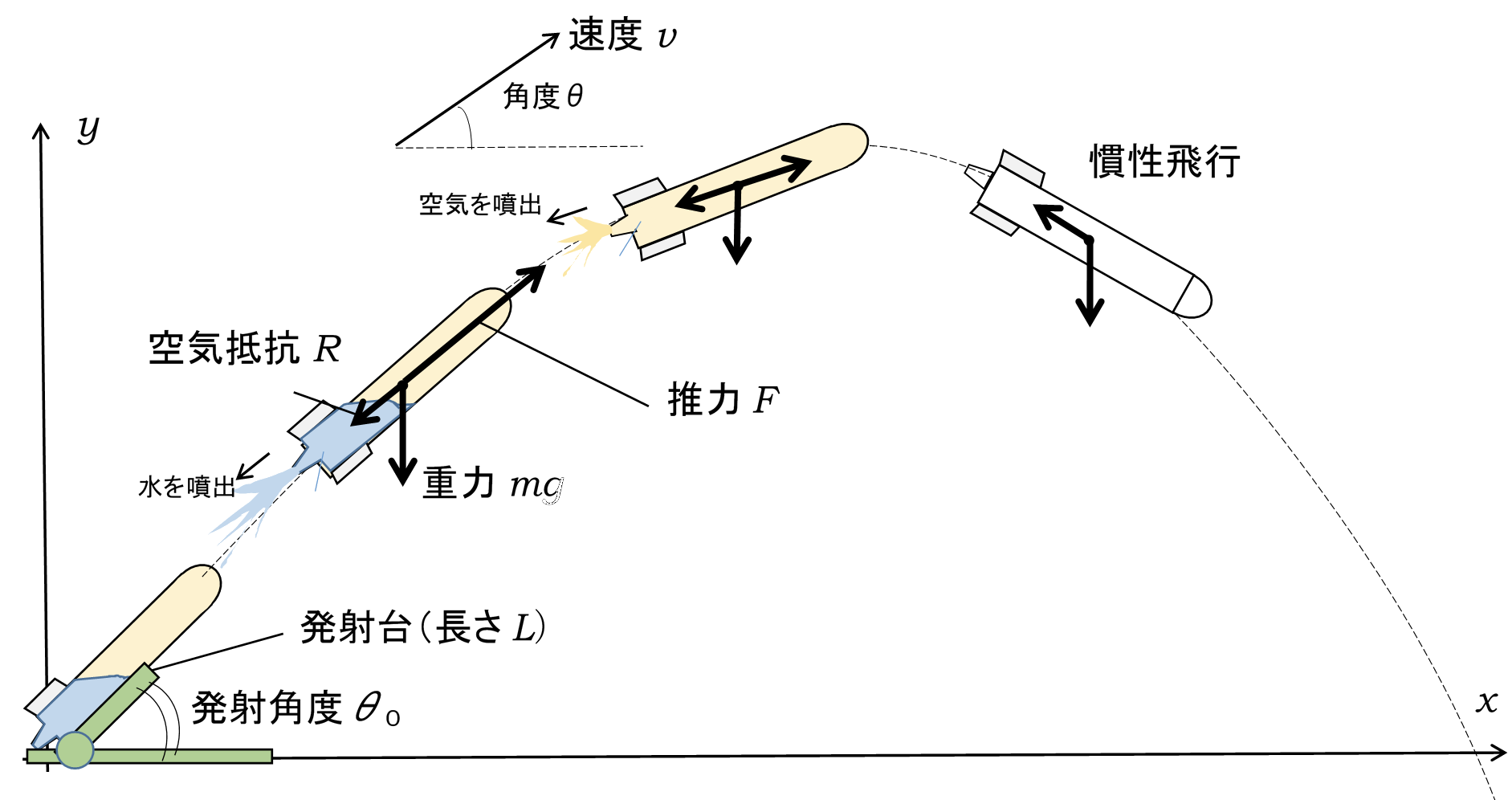
さて、いよいよ最後である。図のように、水を入れたペットボトルロケットを、ある角度\(\theta_0 \)の発射台に設置し、圧縮空気を入れ、水を噴射させロケットを飛ばすことを考える。ロケットにはたらく力は、推力\(F\)、重力\(mg\)、空気抵抗\(R\)である。さらに、発射台に沿って進んでいる間は、発射台から垂直抗力\(N\)を受ける。発射台との間の摩擦力は無視する。ロケットは水を噴出しながら発射台に沿って長さ\(L\)だけ進み、さらに水を噴出しながら飛ぶ。途中で水がなくなると空気を噴出しながら進む。さらに中の空気が大気圧と同じ圧力(1気圧)になったら、あとは慣性飛行(重力と空気抵抗だけがはたらく運動)となる。では、ロケットの運動方程式をたててみよう。
\begin{equation}
m\frac{dv_x}{dt}=(F-R)\cos\theta-N\sin\theta
\end{equation}
\begin{equation}
m\frac{dv_y}{dt}=(F-R)\sin\theta-mg+N\cos\theta
\end{equation}
ここで、\(\theta\)は、ロケットの進行方向と\(x\)軸のなす角度を表している。
ここで、発射台からの垂直抗力\(N\)は、ロケットが長さ\(L\)の発射台の上を進んでいる間は\(N=mg\cos\theta_0 \)、発射台の上を通り過ぎたら、\(N=0\)となる。もちろん、その間は\(\theta =\theta _0\)である。推力\(F\)は、水を噴出している間は、(1−3)節の考え方で、水がなくなり空気を噴出している間は(1−4)節の考え方で求めるものとする。空気が外気圧と同じになった後は\(F=0\)である。
第3章 参考文献
(1)日本ペットボトルクラフト協会編「ペットボトルロケットを飛ばそう」ダイナミックセラーズ出版
(2)松尾喬 編「ペットボトルロケットのつくりかた」英知出版
(3)愛知、岐阜物理サークル「いきいき物理、わくわく実験」新生出版株式会社
(4)前田弘「飛行力学」養賢堂
(5)原田三夫・新羅一郎「宇宙ロケット」共立出版
(6)加藤宏「流れの力学」丸善株式会社
(7)須藤浩三・長谷川富市・白樫正高「流体の力学」コロナ社
(8)谷田好通「流体の力学」朝倉書店
(9)平田邦男「BASICによる物理ドライラボ入門」共立出版