K123.東京都心部の森林(自然教育園)における熱収支解析
著者:近藤純正・菅原広史
東京都港区白金台の森林公園「自然教育園」の樹冠上で6年半にわたり観測した顕熱・潜熱の乱流
フラックスと、長波・短波の下向き・上向きの放射フラックスを解析した。
(1)潜熱輸送量の年平均値は73W/m2(年蒸発散量=940mm/y)である。この値が各地森林の水文
データや、熱収支計算から得られている1980年代の値に比べて10%程度大きいのは、乱流フラックス
の観測は降雨日に欠測が多いこと、東京都心部の近年の温暖・乾燥化によるものである。
(2)晴天日中の熱輸送量が最大になるのは、顕熱は3~5月に300W/m2前後、潜熱は7~8月に
400~500W/m2前後で、ボーエン比の気温依存性・季節変化が明瞭である。(3)晴天日中の顕熱輸送
のバルク係数として高度35mの風速=3~8m/sの範囲でCh=0.004~0.012が得られ、風速が強くなると
小さくなる傾向である。Chから交換速度をもとめると、風速=1~8m/sの範囲で、ga=ChU=
0.020m/s~0.042m/sとなる。
(4)蒸発効率βは気温上昇とともに増加する傾向にあり、着葉の状態(季節)に大きく
依存する。新緑の季節にβ=0.1程度から急激に増加し、盛夏にはβ=0.30(気温30℃前後)
に達する。その後は落葉とともに冬に向かって小さくなる。βが強風時に減少するか否かは、風速 9m/s
以下の範囲では明確ではない。
(完成:2016年2月18日)
本ホームページに掲載の内容は著作物である。
内容(新しい結果や方法、アイデアなど)の参考・利用
に際しては”近藤純正ホームページ”からの引用であることを明記のこと。
更新の記録
2016年2月9日:素案の作成
2016年2月11日:図123.1にプロットを追加、その他の細部に加筆
2016年2月13日:123.6節の改訂(ChのかわりにChUの式を与えた計算)、6節と7節の順番を入れ替え
2016年2月15日:四角の囲み文の解説を4か所追記して、分かりやすくした
2016年2月16日:四角の囲み文の解説を改訂
2016年2月18日:図123.6の下に、G の説明を加筆
目次
123.1 はしがき(林内気温の特徴)
熱収支量の配分比
従来の蒸発散量評価
123.2 観測
123.3 データの品質管理(日平均データ)
123.4 蒸発効率と交換速度
123.5 熱収支の季節変化
(a)熱収支量の日平均値
(b)日中の熱収支量とボーエン比
(c)日中の熱フラックスと風速の関係
123.6 バルク係数と蒸発効率の風速依存性
(d) バルク係数の風速依存性
(e) 蒸発効率の風速依存性
123.7 蒸発効率の着葉前後での違い、蒸発効率の季節変化
(f)着葉前後の蒸発効率
(g)蒸発効率の季節変化
123.8 まとめ
付録
付録1 従来の水収支法とフラックスの直接測定法による熱収支量の違い
付録2 日中のデータの品質管理(10-15時平均データ)
付録3 上向き放射量で定義する樹冠の実効温度Trと露場気温の関係
付録4 熱収支量の敏感度テスト
付録5 放射量観測誤差6 W/m2は実効温度Trの誤差1℃に相当
付録6 日中の熱フラックスと風速の関係(補足資料)
付録7 着葉の前・後の条件一覧表
付録8 月ごとの日中10-15時の晴天条件
付録9 熱収支式を解いて顕熱・潜熱輸送量を計算する方法
引用文献
観測協力者
萩原 信介
123.1 はしがき
熱収支量の配分比
地表面(樹冠面)に入射する放射エネルギー(=日射量-反射量+下向き長波放射量)は4成分に配分
される。森林の樹冠面で観測する場合、これら4成分は上向き長波放射量、顕熱輸送量、潜熱輸送量
(蒸発散量=蒸散量+降雨日の遮断蒸発量)、及び樹冠面から下の林床に向かう顕熱輸送量となる。
このときのエネルギー配分(上向き長波放射量、顕熱・潜熱輸送量)とボーエン比(=顕熱/潜熱)
の違いによって、森林の大気に及ぼす加熱効果が違ってくる。植物の気孔開度は日射量、気温、
湿度などに依存するので、森林の蒸発効率は日変化・季節変化することになる。
これまでに行なってきた研究によれば、空間広さが同じ観測地点における晴天日中の「日だまり効果」
による昇温量と夜間の冷却量は、周囲が樹木で囲まれている場合は、建物で囲まれている場合に比べて
2倍以上も大きい。これは、樹木の葉面群の加熱・冷却効果(顕熱の交換速度:コンダクタンス)
が大きいことによる(「K121.空間広さと気温―日だまり効果のまとめ」
の図121.6、図121.14、図121.15)。
自然林に近い森林の場合、林床の木漏れ日率40%以上の開空間における「日だまり効果」を比べると、
気温が相対的に低い春には気温上昇は+0.8℃前後であるのに対し、高温の夏期には+0.4℃前後で
小さい。その理由の一つは、ボーエン比(=顕熱/潜熱)の気温依存性によるものである。
すなわち、同じ入力放射量のもとでは、低温時ほど地表面温度(樹冠層の葉面温度)が気温に比べて
高くなり、顕熱に変換される割合が大きく大気加熱の効果が大きくなる
(「K115.新宿御苑の気温水平分布(2)」の図115.3)。
大都市に設置されている観測所が樹木に囲まれている場合(例:東京北の丸露場)、気温観測値は
森林環境・気象条件に依存し、おもにビル街からなる都市の気候を十分に代表しないことになる
(「K122.北の丸露場の気温―降雨・日照との関係まとめ」の図122.14)。
研究目的の1
上記のことを定量的に明らかにするために、東京都心部の森林(自然教育園)における熱収支量の
日変化・季節変化を調べる。ボーエン比(=顕熱/潜熱)は低温期に大きく、大気を加熱する顕熱
輸送量は春(3~5月)に大きいことを熱収支観測によって定量的に確認する。
従来の蒸発散量評価
もう一つの問題提起として、森林の潜熱・顕熱輸送量の季節変化を図123.1に示した。黒実線は東京
地域、黒破線は甲府地域を代表するモデル森林における潜熱・顕熱輸送量の季節変化(計算値)である。
上図の緑印と下図の赤印のプロットは本報告で得られる季節変化(観測値)である。
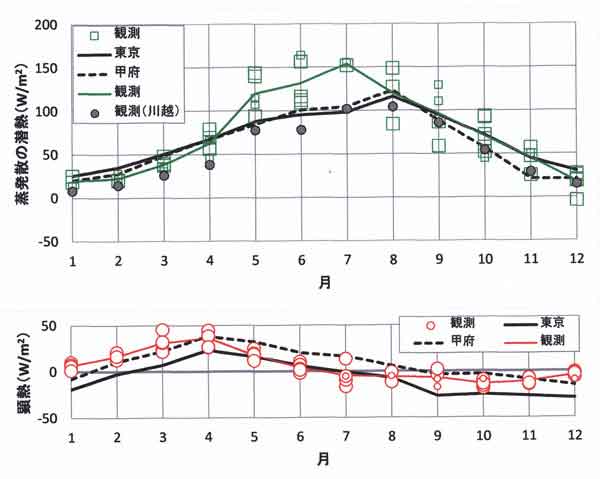
図123.1 森林における潜熱輸送量(上)と顕熱輸送量(下)の季節変化。
黒実線(東京地域)と黒破線(甲府地域)はモデル森林に対する熱収支計算値(1986年~1990年の
平均)。
プロットは自然教育園の樹冠上における乱流変動の観測による直接測定値(2009年7月~2015年12月)。
1か月間の観測日数<15日はプロットせず、観測日数<20日は小印のプロット、20日以上は大印の
プロットで示す。
上図(潜熱輸送量)
緑四角印:観測値
黒実線:計算値(東京地域)
黒破線:計算値(甲府地域)
緑実線:観測値の平均値
黒丸印:観測値(川越、1996年)
下図(顕熱輸送量)
赤丸印:観測値
黒実線:計算値(東京地域)
黒破線:計算値(甲府地域)
赤実線:観測値の平均値
上図の黒丸印は埼玉県川越の落葉広葉樹林で観測された潜熱輸送量の1996年の値、ただし、3月は1997年
の観測値である。この黒丸印は、ボーエン比法による潜熱輸送量である。ただし、日射量が10W/m2
以下の時間帯を除外した蒸発散量の積算値を潜熱輸送量に換算した値である(渡辺、2001;近藤の「地表面に
近い大気の科学」の図7.6)。
しかし、夜間を含む10W/m2 以下の時間帯でも、霧発生時など高湿時を除けば、林内の
水蒸気量の多い空気は林外へ放出(潜熱輸送量はプラス:上向きの)時間帯は多い(後掲の図12.5、図123.6)。
したがって、黒丸印で示す潜熱輸送量の月平均値とそれを換算した年蒸発散量(677mm/y)は小さめに
評価されている。
モデル森林における計算値とは、1986~1990年の5年間の気象官署における日々の気象データと、
地域を代表する地域平均風速 UBを用いた熱収支法による計算値である(近藤・中園・渡辺・桑形、
1992)。これを「1988年計算値」と呼ぶことにする。
また、顕熱輸送量(顕熱フラックス)と潜熱輸送量(潜熱フラックス)を略して「顕熱」、
「潜熱」と表すこともある。日射量と反射量は、それぞれ下向き短波放射、上向き短波放射と
して表す。
備考1:モデル森林における熱収支量の計算値
日本各地の試験流域(東山、桐生、川向、去川2号沢、竜の口北谷)における水収支法による蒸発散量
の観測値と熱収支法による蒸発散量の計算値が一致するように、森林のバルク係数 Chと蒸発効率βが
評価された。すなわち Ch=0.01、降水時の蒸発効率β=1、無降水日の蒸発効率β=0.10(2月)
~0.26(8月)と評価された。この Chとβおよび日々の気象データを用いた熱収支計算によって
日本の66地域の潜熱・顕熱が求められた(近藤・中園・渡辺・桑形、1992)。そのうちの東京地域と
甲府地域の計算値が図123.1に示されている。
備考2:地域代表風速
地域代表風速 UBは、内陸を含むやや広域を対象とした熱収支計算に利用するために考案されたもので
ある。観測地点近辺の固有な地物・地形の影響を取り除き、風速に対する空気力学的粗度
z0=1mの森林上(または都市上)の高度50mに換算した風速であり、水平スケール
100km程度の地域を代表する。その評価の方法は近藤・桑形・中園(1991)によって説明されて
おり、全国66地点の具体的数値は近藤・中園(1993)に示されている。
地域代表風速UBは、次の関係がある。
UB=αmeanU50
αmean=0.67:日本全域の平均的な地形効果による風速の減衰係数(106地点の平均)
U50 :地形の影響を受けない無限に広い粗度1mの水平一様地表面の高度50mの風速
図123.1に示された計算値と観測値には次の違いがある(詳細は付録1)。
(1)5~7月に注目すると、「1988年計算値」に比べて潜熱フラックスの観測値は大きいのに対し、
顕熱フラックスの観測値は小さい。この傾向は、熱収支理論によれば、計算に用いた蒸発効率
「0.10(2月)~0.26(8月)」よりも5~7月の蒸発効率は大きいことを意味する(Kondo & Watanabe,
1992;「水環境の気象学」の図6.3)。
いっぽう、1~3月は逆になり、潜熱フラックスの観測値は小さいのに対し顕熱フラックスの観測値
は大きい傾向にある。これは計算に用いた蒸発効率「0.10(2月)~0.26(8月)」よりも1~3月の
蒸発効率が小さいことを意味する。
このことは123.6節「蒸発効率の着葉前後での違い、蒸発効率の季節変化」で確認される。
(2)「1988年計算値」に比べて潜熱フラックスの観測値が大きい傾向にあるのは大都市・東京の
温暖・乾燥化と関係がある。1960年以後の年平均湿度は、1年につき0.1%の割合で減少しており、
この割合を1988年から2013年までの25年間に換算すると2.5%の乾燥化となる。あるいは、
1986~1990年の5年間平均湿度に比べて2011~2015年は2.6%減少している(付録1)。
この乾燥化によって、今回の潜熱輸送量(蒸発散量)の観測値は大きくなる可能性がある。
最近の25年間の東京の都市化にともなう気温上昇(0.5℃)と湿度減少(3%)による蒸散量は
おおよそ5%ほど増加する(付録4の敏感度テストを参照)。
なお、相対湿度の減少は気温が上昇したことのほか、都市化による水蒸気発生源の縮小にによるもの
である。
(3)潜熱フラックスは全体として観測値が計算値より大きい傾向にある。これは降雨時の観測値
(遮断蒸発量)が時々欠測になり、観測値はおもに無降雨日の観測(蒸散量)を多く含むこと
による。
そのため、顕熱・潜熱輸送量の月・年平均値の評価では、直接測定値の欠測を補完するために
熱収支法による計算が併用されることになる。その際、対象とする森林の交換速度(ga
=ChU)と蒸発効率(β)について、正しい値を知る必要がある。
研究目的の2:
東京都心部の森林(自然教育園)における顕熱の交換速度 ChU(コンダクタンス)と蒸発効率βを
知ることである。あるいは、ChU と平均風速 U からバルク係数 Ch をもとめることである。
蒸発効率をもとめる2つの方法:
森林の蒸発効率は2つの方法でもとめる。それらは、123.4節と123.5節(c)で説明される。
(1)前者では、樹冠の葉面温度(樹冠代表温度)と気温の差δT、および顕熱・潜熱フラックス
の3要素の観測値を用いる。その際、δT の観測値にあいまいさを含む(123.4節)。
(2)後者では、δT の観測値は用いず、気温Tと蒸気圧Vpを用いる。熱収支式からTr(樹冠葉面
の有効温度:林内の樹体・林床の温度も含む)と顕熱H・潜熱lEの3つを計算する。この計算値
(HとlE)と観測値(HとlE)の比較から蒸発効率をもとめる(123.5節 c )。
直接測定の欠測を補完する方法
ー熱収支法による顕熱・潜熱フラックス評価の具体的方法ー
(1)熱収支法で計算する際に必要な条件(入力パラメータ)は、
有効入力エネルギー Q(=入力放射量-G)、気温、蒸気圧、風速 U(または交換速度 ChU)、
および蒸発効率βである。ここに、G は葉面層からの下向き顕熱フラックスである。欠測
時は G のデータはないので、推定値を用いる。
交換速度として式(9)を用いる。蒸発効率βは図123.15(下)の
緑線を用いる。風速は高度35mの気象庁北の丸の観測値 U を用いる。自然教育園の高度20mの
風速 U20を用いる場合は、U=1.8×U20 を用いる。
降雨時で葉面が十分に濡れたと判断される時間帯には、β=1を用いる。
(2)計算で得られる結果(出力)は、
顕熱フラックス、潜熱フラックス(蒸発散量)、有効地表面温度 Te の3つである。
参考:Te は有効な樹冠葉面層の温度であり、葉面群の放射温度の平均値に近似的に等しいが、
現実には測定は難しい。なぜなら、放射温度計では、直射の当たっている葉面とそうでない
葉面温度や、森林の上部・下部層の葉面温度の平均値を測定することになるが、その放射温度
は樹冠層上面の数m上で観測される顕熱・潜熱フラックスを必ずしも十分に代表するとは限ら
ないからである。つまり、森林は水面や裸地面などと違って地表面温度の定義が複雑である。
|
図123.1からわかること
ー東京都心部の自然林における蒸発散量ー
(1)1990年代に熱収支計算法によって評価してあった東京の「1988年計算値」は、当時の東京
大手町の気象データを使って得た結果であり、位相のずれはあるが、森林からの蒸発散量を
かなりよく再現している。
(2)熱収支式を解く方法では、顕熱・潜熱フラックスの風速依存性は大きくないので、
気温と蒸気圧と入力放射量に大きな差がなければ、顕熱・潜熱フラックス(蒸発散量)に
おける違いはわずかである。
(3)東京都心部の自然林における今後の蒸発散量は地球温暖化と都市気候変化によって
変わってくると考えられる。
(4)明治神宮の森もほとんど自然林であり、場所・環境も自然教育園に近く、蒸発散量も
ほとんど同じ値と考えてよいだろう。
|
123.2 観測
顕熱・潜熱輸送量、および短波・長波の上向き・下向き放射量は東京都港区白金台の自然教育園の
ほぼ中央の自然林の中に建てられた高さ20mの観測塔で観測した。
観測塔周辺の樹木の平均的な高さは14mである(直近で16mの樹木 もある)。この周辺の樹種は、
おもに高木スダジイ、亜高木ヤブツバキ、トウネズミモチ、およびコナラ(落葉樹)からなる。
この公園は、自然森林に近い状態にある。
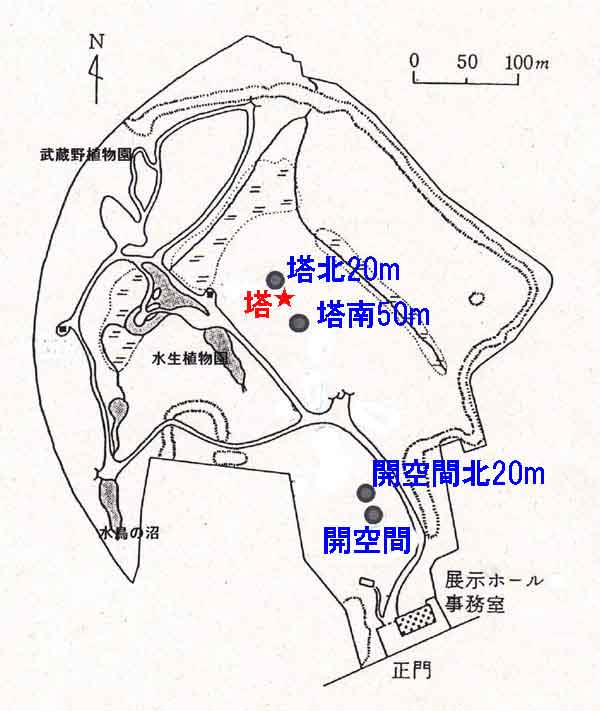
図123.2 自然教育園の地図、塔はフラックスの観測地点(赤星印)。
「塔北20m」、「塔南50m」、「開空間北20m」、「開空間」は2015年3月12日 ~6月4日の
観測点である(「K117.自然教育園の林内気温-6月~10月」の図117.1に同じ)。
測器の一覧は表123.1に示した。
表123.1 測器の一覧 (設置高度はいずれも地上高20m)
観測要素 測 器
顕熱フラックス 超音波風速計(ソニック SAT-550)
潜熱フラックス 超音波風速計(ソニック SAT-550)+水蒸気変動系(LICOR L17500)
短波・長波放射量 KIPP&ZONEN CNR-1(下向き、上向き短波と長波の4成分放射計)
風向・風速 超音波風速計(ソニック SAT-550)
気温 白金抵抗温度計(ヴァイサラ HMP-110)+ 縦型強制通風管
湿度 静電容量式湿度計(ヴァイサラ HMP-110)+ 縦型強制通風管
* 音速は気温のほか水蒸気量の関数である。したがって超音波風速計による気温は、
音仮温度を観測することになる。本観測では、水蒸気量の影響を補正した気温の真値
を用いた顕熱輸送量である。
観測データは2009年7月18日か2015年12月17日までの6年半(2341日間)を解析する。
観測項目は風向、風速、気温、湿度、顕熱、潜熱、短波・長波の下向きと上向き放射量の10要素
である。各要素について30分単位の平均値一覧表を作成した。
10要素×2341日×(24時間×2)=1,123,680データ
となる。この一覧表をもとにして、日平均値の表と日中の平均値(10時-15時)の表を作成し、
それぞれ日平均と日中平均について熱収支解析を行う。
観測装置の故障・交換などがあり、2341日間で有効なデータが得られた総日数は2151日である(92%)。
次節で示すように、観測データの品質管理を行い、誤信号などはデータ無しとして取扱い、
有効なデータは2151日間より少なくなる(観測要素によって異なる)。
123.3 データの品質管理
乱流フラックスの観測では、誤信号がしばしば発生する。データの品質管理が不十分
だと、熱収支式に大きなインバランスが生じる。
日平均データについて、誤信号データは次の順序で除去した。なお、日中(10-15時)平均データ
についての誤信号の除去は別方法による(付録2)。
(1)データ一覧表(10万行余)を数回にわたり目視し、例えば熱フラックス量に換算したとき
10000W/m2 のような異常値、長時間にわたり例えば風速=0.3m/sの継続、氷点下10℃以下の
気温が長時間継続するような明らかな誤信号は除去して、データ無しとする。
(2)日降水量>10mmの日について、日平均値の乱流フラックス(顕熱、潜熱)、及び下向き長波
放射量は除去し、データ無しとする。(ただし、123.5節の(b)以後の日中10-15時平均値に
ついては、降雨中でも明らかな誤信号と認められる場合以外は有効データとして用いる。)
(3)見落としデータがあるので、時系列グラフを描き、前後に比べて異常値と思われるデータは
削除する。あるいは、上向き長波放射量など推定が容易な要素については前後の平均値で補正する。
(4)日平均値について、熱収支量の残差は樹冠面から下層への顕熱フラックスである。
下向き・上向き短波放射をS↓・S↑、同様に長波放射をL↓・L↑とすれば、
樹冠面から下層への顕熱フラックス:G=(S↓-S↑+L↓-L↑)-(H+lE)
で表される。これを熱収支インバランスとする。このインバランスの年平均値はほぼゼロにならねば
ならない。これを確かめるために、6年間半のグラフに描くと、2013年の夏に大きなギャップが
見られる。その前後について、インバランスの長期平均値は、
前半期間:2009年7月~2013年7月22日まで・・・・+35W/m2
後半期間:2013年8月7日~2015年12月まで・・・・-1W/m2
である。
このギャップは落雷によって測器が壊れて交換した前後に相当する。
大きなインバランスが生じた原因を探るために、まず、日射量S↓について、北の丸公園の科学技術館屋上で観測している気象庁の観測値S↓(北の丸)と比較する。6年間半について両地点の日射量の比S↓/S↓(北の丸)の時系列を描くと、2013年7月以前の平均値は1.1前後であり、2013年8月以後の平均値はほぼ1.0である。
北の丸の日平均日射量>100W/m2 の条件について日射量の比を計算してみると、
前半期間:2009年7月~2013年7月22日・・・・S↓/S↓(北の丸)=1.10
後半期間:2013年8月7日~2015年12月・・・・S↓/S↓(北の丸)=1.02
となる。気象庁北の丸の観測値の精度について確かめてないが、本研究では前半期間の自然教育園
における日射量観測値を10%小さく補正することにした。
以上の補正を施すと、インバランスの平均値は、
前半期間:2009年7月~2013年7月22日まで・・・・+17±23W/m2
後半期間:2013年8月7日~2015年12月まで・・・・-1±24W/m2
となった。偏差(±23 W/m2、±24W/m2)の大きさは、解析データの
プロットにおけるバラツキの目安となる。
その他の熱収支量について吟味したが、大きな誤観測は見つけられない。日平均値データについて
(1)~(4)の品質管理を行った結果を以下の図で示す。
図123.3(上)は樹冠面から下層への熱フラックス(日平均値)の経時変化である。後半期間には
インバランスの平均値はほとんどゼロであるが、前半期間には0~50W/m2 の間に分布
しており、平均値17W/m2 程度は放射フラックスと乱流フラックスを総合したときの誤差とみな
される。
下図は日平均日射量の経時変化であり、±10W/m2 を超えるような誤差は見出し難い。
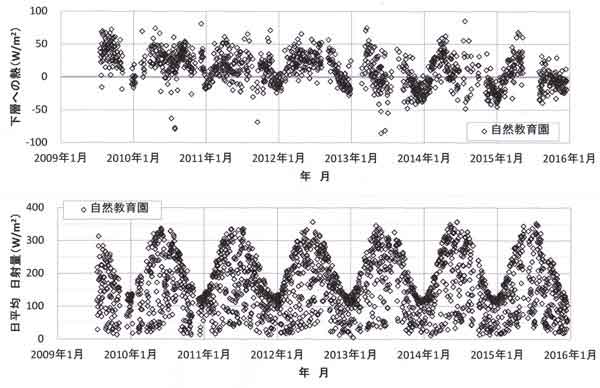
図123.3 日平均熱収支バランス(上図)と日平均日射量(下図)の経時変化、2009年7月~
2015年12月。
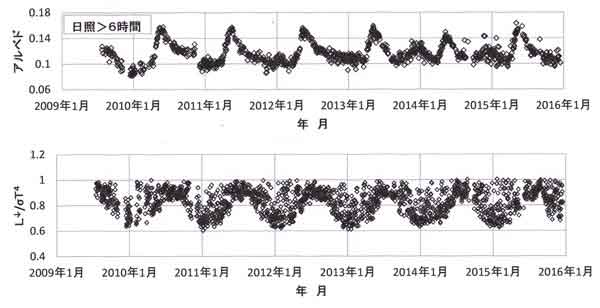
図123.4 アルベド(上図)と大気放射量(下図)の経時変化、2009年7月~2015年12月。ただし、
上図には日照時間>6時間のみをプロットしてあり、下図の大気放射量L↓は日平均気温Tに対する
黒体放射量で割算した規格化値をプロットしてある。
全期間のアルベドの平均値=0.116
である。アルベドは4下旬~6月上旬の新緑の季節に0.14~0.15に上昇し、秋~春の落葉期に
0.10~0.12に低下している。
落雷を境とする前半期間には目立たないが、後半期間の2014年と2015年の1月のアルベドが上昇する
傾向に見えるのは、両期間のいずれかの期間の日射計がわずかに傾斜している可能性がある。
アルベド0.01の誤差は、冬期晴天日の日平均日射量120~130W/m2 のうちの10W/m2
程度の誤差に相当する。
晴天日中の太陽高度の平均値が30°の場合、日射計が正常な設置に比べて1°傾斜している
場合の誤差は概略15W/m2 に相当する。
図123.4(下)は規格化した日平均大気放射量の経時変化であり、明らかな誤信号など除去した
品質管理の結果として縦軸は1以下となっている。縦軸が小さい値は快晴に近い日であり、
水蒸気量の多い夏期には0.85程度、水蒸気量の少ない冬期には0.6程度を示し妥当な値である
(「地表面に近い大気の科学」の図2.23を参照)。
誤差があるとすれば、縦軸の値で0.02程度またはそれ以下であり、放射量に換算すると
±10W/m2 程度に相当する。
以上の検討により、品質管理後の短波・長波の放射量の誤差は10W/m2 程度、または
それ以下と考えられる。
乱流フラックス(顕熱、潜熱)については、異常値や大雨時は前述のようにデータ無しとしたが、
10~20W/m2 程度の誤差の判別は難しい。年平均の熱収支のインバランス
(樹冠面から下層への熱フラックス)の平均値(+17W/m2程度)が放射フラックスと
乱流フラックスを総合したときの誤差とみなすことにする(前半期間)。後半期間については、
インバランスの平均値は概略ゼロであるので、総合したときの誤差は±10W/m2 程度、
またはそれ以下とみなしてよいだろう。
以上は、日平均値データの品質管理を述べたもので、日中(10-15時)平均の品質管理については
付録2に説明されている。
備考3:地表面のアルベドと日射量
日射量(直達光と散乱光)のうち、散乱光には地表面で反射された太陽光が大気中で散乱されて
地表面にくる成分も含まれる。それゆえ、日射量は観測地点周辺のアルベドに依存する。
アルベドが0.1大きくなれば、快晴時の日射量は概略2%大きくなる(「水環境の気象学」のp.87)。
気象庁の観測は森林公園内の科学技術館屋上で行われているので、アルベドの違いによる自然教育園
での日射量との違いは1%以下であり、無視してよい。
123.4蒸発効率と交換速度
品質管理後のデータを解析する。平均風速については、地域代表風速(高度50m)を用いた
「1988年計算値」と比較するために、観測高度の高い気象庁の北の丸公園における風速(測風塔
地上高=35m)を用いる。なお、自然教育園における風速(地上高=20m)は北の丸の風速の
およそ半分である(「K117.自然教育園の林内気温、6月~10月」
の付録を参照)。
この節では、連続晴天日に観測されたデータを用いて、森林の蒸発効率と交換速度を評価する。
連続晴天日における熱収支量の日変化を図123.5(2015年8月1日~7日の平均値)と図123.6に
(2015年10月7日~8日の平均値)、また図示しない要素は表123.2に示した。
表123.2 連続晴天日に観測された主な要素の一覧表(その他の要素は表123.3)。
8月1日~7日 10月7日~8日
10~15時 日平均値 10~15時 日平均値
高度19mの気温T ℃ 32.78 30.04 21.68 18.70
正味放射量Rn W/m2 640 199 506 94
下向き長波放射L↓ W/m2 443 424 308 297
上向き長波放射L↑ W/m2 500 478 429 408
下向き短波放射S↓ W/m2 786 286 700 231
上向き短波放射S↓ W/m2 89 34 73 27
アルベド S↓/S↑ 0.11 0.12 0.10 0.12
L↑の黒体放射の温度Tr ℃ 33.23 29.80 21.80 18.10
Tr-T ℃ 0.45 -0.24 0.12 -0.60
湿度 % 59 69 30 40
蒸気圧hPa 29.4 29.4 7.8 8.6
風速 m/s 1.88 1.58 3.41 2.79
北の丸風速 m/s 4.05 3.05 6.00 4.42
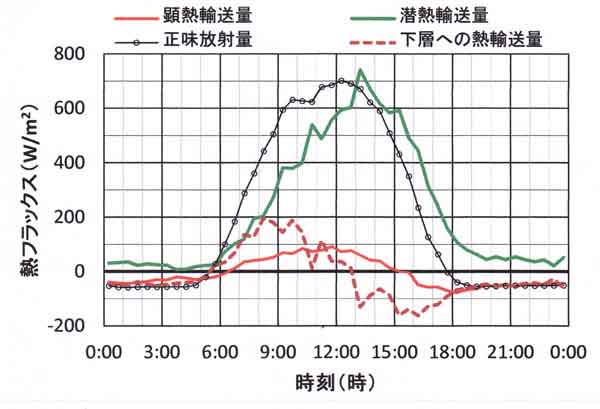
図123.5 熱収支量の日変化、2015年8月1日~7日(7日間平均)。
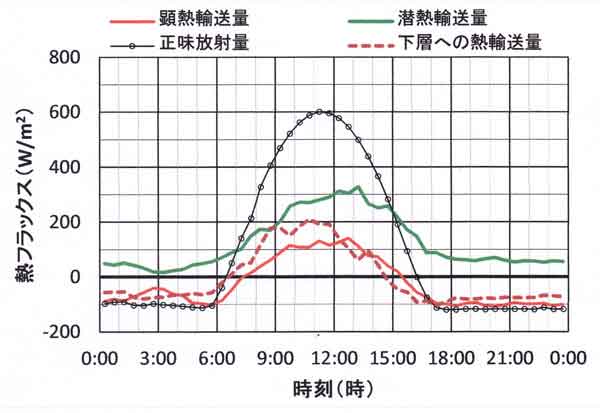
図123.6 熱収支量の日変化、2015年10月7日~8日(2日間平均)。
高温の盛夏(図123.5)と秋(図123.6)を比べると、盛夏には日中の潜熱は正味放射量に匹敵する
大きさであるのに対し、秋はおおよそ半分で小さい。一方、正午ころの顕熱に注目すると、
盛夏には100W/m2に達していないが、秋には100 W/m2を超えている。
これはボーエン比の気温依存性によるものであり、すでに前節でも示したとおりである。
両図の褐色破線は樹冠面から下向きの顕熱輸送量 G である。おもに正午前の日中の短時間は200W/m2、
夜間の長時間はマイナス(上向き)50~100W/m2である。
日中のプラスの値 G は、樹冠上面から下向きに運ばれ、林内の樹体(葉面、小枝、幹の表皮から約0.1mまでの
厚さ)の温度上昇と林床下の表層土壌(地中約0.1mまで)の温度上昇に使われる。夜間の G はマイナスであり、
林内から樹冠上面へ運ばれてくる顕熱輸送量、すなわち樹体と表層土壌の温度下降による熱エネルギーである。
観測塔の周辺は必ずしも水平一様ではないので、G の一部のわずかの量は、林床面上の微風によって観測塔
周辺との間で水平方向の移流熱交換も行なわれている可能性がある。
次に、樹冠層の蒸発効率β(無次元)と交換速度 ChU (単位はm/s: ga=ChUで表すこともある)
について、晴天日の日平均データと晴天日中の10~15時平均のデータを用いて評価する。この際、
樹冠の葉面温度と気温の差δTは±2℃以内にあるので熱収支式の近似解法にしたがい、顕熱(H)・
潜熱(lE)と温度差(δT)の観測値が正しいとして、それらの計算値(H, lE, δT)との差が
最小になるときのβと ChU の最適値をもとめる。
熱収支式の近似解法は「水環境の気象学」の式(6.33)~(6.35)を用いる。樹冠の葉面温度
(樹冠代表温度)の観測値を Tsとして、日平均値は上向き長波放射量に相当する黒体放射
温度 Trを用いる(備考4)。
なお、精度の高い逐次近似法は付録9で説明されている。
一方、日中のデータについては上述の方法が利用できない。その理由は、日中の林内気温が複雑な
鉛直分布であることによる。そのため、上向き長波放射量は樹冠層の下の低温の日陰からの放射の
寄与も一部含み、厳密には樹冠の葉面温度を代表しないからである。
備考4:樹冠の葉面温度(樹冠代表温度)
熱収支式による樹冠代表温度 Tsと顕熱・潜熱フラックスの計算値と、それらの観測値との比較から
交換速度と蒸発効率をもとめる場合、Tsの観測値は、通常、樹冠上から放射温度計で斜め方向に
測った温度を用いるのだが、本研究では観測していないので、工夫がいる。
観測塔の周辺は比較的密な森林であるが、完全に密でないために樹冠の上で観測される上向き
長波放射量には、樹冠代表温度のほか林床までの下層の低温度からの長波放射量も一部含まれる。
なお、森林の植生密度が密でない中間密度のときは、Tsの決め方はあいまいになり、バルク係数 Ch の
定義は難しく、有効温度を用いることになる(Kondo & Watanabe,1992; 「水環境の気象学」の
9.4.5「フラックスの評価法」を参照)。
樹冠の葉面温度と気温の差δT
〇日平均値について
観測によれば、林内における日平均気温の鉛直分布は高度20mの気温 Tより低温の安定成層である
(「K117.自然教育園の林内気温―6月~10月」の図117.9を参照)。
それゆえ、上向き長波放射量で定義される黒体温度 Trを樹冠の葉面温度(樹冠代表温度)Ts と
して代用し、温度差を次式で定義する。
日平均の温度差:δT=Ts-T≒Tr-T ・・・・・(1)
自然教育園の20m観測塔の周辺では、通常、δT はマイナス値として観測される。
〇日中の平均値(10時~15時)について
日中の気温鉛直分布については、平均樹高(14m)の付近で極大気温となっており、それより
下層で低温の安定成層である(「K117.自然教育園の林内気温―6月~10月」
の図117.9を参照)。
それゆえ、樹冠代表温度TsはTrよりも若干高くなり、Tsは Trで代表することはできない。
例えば、8月1~7日の日中の Tr-T=0.45℃であるが、この差は Ts-Tよりも小さく観測されている
はずである。
5月に平塚市内で観測した葉面・気温差の観測例(5月6日:2.1℃、5月9日:1.2℃、5月29日:2.1℃)
の平均値は、
5月の晴天日中の観測温度差:δT=Ts-T=1.8℃ ・・・・・(2)
である(「K83.気温観測に及ぼす樹木の加熱効果―実測」)。
高温の夏期には熱収支の特徴から温度差は小さくなるので、
夏期の温度差(仮定):δT=Ts-T=1.0℃ ・・・・・・(3)
と仮定する。なお、正確にはδTは風速に依存する。
表123.3は連続晴天日の2015年8月1~7日と10月7~8日の観測値に基づいて求めた交換速度、蒸発効率、
その他データの一覧表である。
表123.3 連続晴天日のデータの一覧と、交換速度、バルク係数、蒸発効率の計算
結果。
晴天期間 8月1日~7日 10月7日~8日
観測値 計算値 観測値 計算値
10-15時 入力放射 W/m2 R↓ 1140 934
下向き顕熱 W/m2 G -2 120
有効エネルギー Q 1142 814
気温 ℃ T 33 21
相対湿度 rh 0.60 0.33
蒸気圧 hPa Vp 29.4 7.8
蒸発効率 β 0.29 0.18
交換速度 m/s ChU 0.050 0.045
北の丸風速 m/s U 4.05 6.00
Ts-T δT 1.00 1.02 1.80 1.80
顕熱 W/m2 H 59 62 102 97
潜熱 W/m2 lE 578 579 283 282
バルク係数 Ch 0.012 0.0075
ボーエン比 H/lE 0.10 0.11 0.36 0.34
日平均 入力放射 W/m2 R↓ 676 501
下向き顕熱 W/m2 G -17 -5
有効エネルギー Q 693 506
気温 ℃ T 30 19
相対湿度 rh 0.69 0.40
蒸気圧 hPa Vp 29.4 8.6
蒸発効率 β 0.29 0.18
交換速度 m/s ChU 0.035 0.031
北の丸風速 m/s U 3.05 4.42
Ts-T δT -0.24 -0.22 -0.60 -0.61
顕熱 W/m2 H -9 -7 -26 -27
潜熱 W/m2 lE 224 222 125 124
バルク係数 Ch 0.011 0.0070
ボーエン比 H/lE -0.04 -0.03 -0.21 -0.23
この節では観測値(H, lE, δT)が熱収支法による計算値と矛盾しない最適値の蒸発効率βとバルク
係数 Ch を評価した。その際、δT の観測値にあいまいさを含んでいる(付録5を参照)。
そこで、δT に0.5℃の誤差を含む場合、βとCh の評価にいかほどの違いが生じるか、敏感度テスト
を行なった。表123.4によれば、気温が33℃の8月におけるβの違いは0.15、気温が21℃の10月に
おけるβの違いは0.05である。
表123.4 δTが0.5℃低いときの蒸発効率βとバルク係数Chに及ぼす敏感度テスト。
8月1日~7日はδT=1.0℃を0.5℃とし、10月7日~8日はδT=1.8℃を1.3℃
としたときのβ、ChU、Chの変化を → の値で表してある。
8月1日~7日(10~15時) 10月7日~8日(10~15時)
気温 T(℃) 33 21
温度差 δT(℃) 1.0 → 0.5 1.8 → 1.3
蒸発効率 β 0.29 → 0.14 0.18 → 0.13
交換速度 ChU(m/s) 0.050 → 0.111 0.45 → 0.064
バルク係数 Ch 0.012 → 0.027 0.0075 → 0.011
「水環境の気象学」の図6.3からもわかるように、水面(β≒1)など蒸発効率が1に近い地表面
では、βに誤差が0.1程度あっても熱収支量に大きな影響を及ぼさないが、森林など蒸発効率が
小さいβ=0.2~0.3の地表面ではβの精度は±0.02程度は必要である(気温が20℃の場合、
熱収支量の誤差は概略±10W/m2)。
表123.4によれば、気温が21℃のときのβの誤差0.02に対するδTの精度≒0.2℃でよいが、特に
高温時の夏の精度は0.1℃が必要であることがわかる。高精度通風筒を用いた気温観測の精度0.03℃は
可能としても、樹冠の葉面温度(樹冠代表温度)の観測精度として0.1℃は難しい。
それゆえ、本節(表123.2)で求めた蒸発効率βと交換速度ChUとバルク係数Chは、観測例も少ない
こともあり、不確実性を含む。バルク係数については、晴天日の値(0.012、0.0075)と日平均
の値(0.011、0.0070)から、次のようにまとめることができる。
連続晴天日の観測から得た森林の交換速度とバルク係数と蒸発効率:
交換速度 ga=ChU=0.031~0.050m/s(U=3.1~6.0m/s)・・(4)
バルク係数Ch=0.007~0.012 ・・・・・・・・・・・・・・・・・・・(5)
蒸発効率 β=0.29(8月、33℃) ・・・・・・・・・・・・・・・・(6)
蒸発効率 β=0.18(10月、21℃) ・・・・・・・・・・・・・・・ (7)
Ch=0.007~0.012は、日本各地の森林において水収支法で求めた降雨日の遮断蒸発量の観測値が
再現できる標準林のCh=0.008(近藤・渡辺・中園・石井、1992)、あるいは水収支法による蒸発散量
の季節変化の観測値が再現できるCh=0.008~0.011と対応している(近藤・渡辺・中園、1992)。
式(4)~(7)は、後述の別方法によって得られるCh、βと比較できる。
熱収支式を解く方法、その1
ー温度差を重視する場合の計算ー
熱収支式を解く方法によって顕熱・潜熱フラックスを求めることができる。
通常は、バルク係数Ch(または交換速度ChU)と蒸発効率βが既知として
熱収支式から地表面と気温の差δT、顕熱フラックス H、潜熱フラックス lE の3つを求めることが
多い。
ここでは、その逆で顕熱・潜熱の観測値がわかっているので、交換速度と蒸発効率を計算
から求めた。その際に、潜熱・顕熱フラックスに多少なりとも誤差を含むので、
観測値と計算値がもっとも合う最適値の交換速度と蒸発効率を求めたことになる。
この節では、計算から得られるδT、H、lE のうち、δTを重視することとした。その理由は、
本計算条件では H 、lE の変動幅が大きいのに対し、δT の変動幅が相対的に小さいからで
ある。
ところが森林の場合は、水面や裸地面のように地表面温度の定義が明確ではない。その理由は、森林
は葉面群からなる複雑な多層構造であるからである。密な森林の場合、上向き長波放射量を
黒体温度に換算した値を地表面温度(樹冠層の平均的な温度)とみなせるが、近似が
悪いこともあり、曖昧さを含む。
なお、後の節では、地表面温度を重視せずに(δT を用いずに)、交換速度と蒸発効率を求める
ことになる。
|
123.5 熱収支の季節変化
(a)熱収支量の日平均値
2009年7月18日から2015年12月17日までの6年半にわたる2341日間で有効なデータが得られた
総観測日数は2151日である(92%)。そのうち、有効な日平均潜熱データが得られた日数は62%で
もっとも少なく、次いで日平均顕熱データが得られた日数は76%である。
その他要素の日平均値について風向は94%、風速は92%、気温は90%、相対湿度は93%、
大気放射量は87%、日射量(下向き短波放射)と上向き短波放射および上向き長波放射は100%である。
潜熱データが少ないのは、降水日に誤信号(明らかな誤信号と、大雨日のデータ無しとみなした
観測値)が多いためである。以下の図では有効なデータのみがプロットされている。
図123.7は2012年~2015年の4年間の日平均熱収支量の季節変化である。樹冠面への入力放射量R↓
(=日射量S↓-反射量S↑+下向き長波放射量L↓)は、上向き長波放射量L↑と顕熱・潜熱
フラックス(H、lE)、および樹冠層から下向きの林床に向かう顕熱輸送量 G(下向きを正)
の4成分に変換される。
各々の熱収支量は晴天日に大きく、曇天・雨日に小さい。この図に示された大きな特徴は
(図123.1も参照)、入力放射量と上向き放射量は7~8月に最大であり、蒸発散の潜熱は4~5月から
増加しはじめ、梅雨明け後に大きくなる。大気を直接加熱する顕熱は3~4月に大きいが、他の月は
ゼロに近い小さな値である。
なお、月単位でまとめた潜熱と顕熱は、すでに123.1節「はしがき」の図123.1に示した。
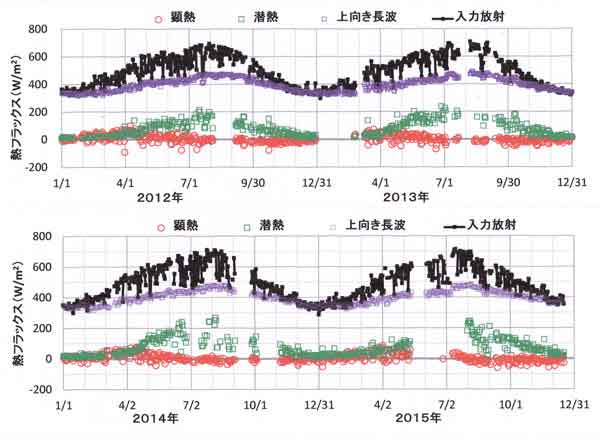
図123.7 日平均熱収支量の季節変化(2012年~2015年の4年間)。
顕熱Hまたは潜熱lEの欠測日も含めると、2009年~2015年の6年半の平均値は:
H=2 W/m2、lE=73 W/m2(蒸発散量=2.58mm/d=78mm/月=940mm/y)、
S↓=171 W/m2、S↑=19 W/m2、下向き長波放射量L↓=344 W/m2、
L↑=400 W/m2、G=22 W/m2である。
G=13 W/m2は熱収支式の残差であるが、ときどき欠測のあるHとlEがともに観測された日
についての平均値である。13 W/m2は全期間の観測誤差(熱収支のインバランス)と
みなしてよい。
後半期間(落雷後の2013年8月7日~2015年12月17日)の平均値は:
H=-1 W/m2、lE=72 W/m2(蒸発散量=2.54mm/d=77mm/月=927mm/y)、
S↓=156 W/m2、S↑=19 W/m2、下向き長波放射量L↓=343 W/m2、
L↑=400 W/m2、G=-1 W/m2であり、熱収支量の残差はほとんどゼロ、
熱収支式は閉じているとしてよい。
今回の乱流フラックス観測による蒸発散量=927~940mm/yについて、水収支法による森林における蒸発散量の観測値(「水環境の気象学」の図14.6)、および熱収支法による「1988年計算値」(近藤・中園・渡辺・桑形、1992)と比較してみよう。
宮崎県去川2号沢:889mm/y, 岡山県竜の口山北谷:835mm/y, 滋賀県桐生:771mm/y, 愛知県
東山:730mm/y, 同白坂:849mm/y, 同穴の宮:639mm/yである。「1988年計算値」では、
東京地域:877mm/y, 甲府地域:833mm/yである。これらに比べて、本研究の自然教育園の蒸発散量
の観測値は10%程度大きい。
本研究の潜熱輸送量(蒸発散量)の観測値が大きい主な理由として、
(1)乱流フラックスの観測は、降水日に欠測が多い
(2)自然教育園は都心部にあり、都市化による高温・乾燥化の影響
が考えられる。高温・乾燥化による蒸発量の増加は、近年25年間に5%程度である(付録4)。
(b)日中の熱収支量とボーエン比
この項では、日中(10-15時)平均の熱収支について解析する。付録2で示したデータの品質管理を
行った結果、使えるデータ個数は次のとおりである。2010~2015年の6年間(2191日)のうち有効
日数は2005日(92%)である。
そのうち、潜熱の有効日数がもっとも少なく74%、顕熱は88%である。そのほか、風速は89%、
気温は90%、相対湿度は95%、短波・長波の放射量は100%である。晴天日(日照率100%、
正味放射量>300W/m2)の有効な解析日数は、顕熱336日、潜熱293日である。
解析の結果、樹冠面から下層への顕熱フラックスG(熱収支の残差)は次のとおりである
(プラスは下向きを表す)。
日中(個数=2005日): G=+112±70 W/m2
晴天時(個数=337日): G=+151±70 W/m2
ここに晴天時とは10-15時の日照率=100%、正味放射量Rn>300 W/m2の条件
である。
日中の G 値は、林内樹体の温度上昇と林床下の表層土壌の温度上昇に使われる。夜間の G はマイナスであり、
樹体と表層土壌の温度下降による熱エネルギーである。晴天日の日中の G(=151W/m2) が
曇天・雨天も含む日中の G(=112W/m2)に比べて大きいのは、晴天日の林内と林床下表層土壌の
温度変化の幅が大きいことを意味している。
図123.8は日中(10~15時平均)の熱収支量の季節変化である。この図には、熱収支の特徴が、
日平均値について示した前図123.7よりも鮮明に現れている。
各熱収支項が小さいのは降雨・曇天日であり、大きいのは晴天日である。晴天日中の顕熱は3~5月に
大きく、潜熱は7~8月に大きくなる。顕熱は3~5月に潜熱を超えているが、それ以後は逆になって
いる。これはボーエン比(顕熱/潜熱)の気温依存性によるものである。
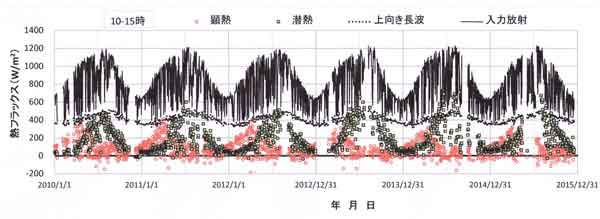
図123.8 日中(10-15時)平均の熱収支量の季節変化(2010年~2015年の6年間)。
この関係をより見やすくするために、晴天日(10~15時の日照率=100%、正味
放射量 Rn>300W/m2)を選び出すことにしよう。日照率=100%は快晴または日射が
比較的に大きい薄雲の条件である。
図123.9は晴天日の顕熱・潜熱の季節変化(上図)とボーエン比の季節変化(中図)である。熱輸送量
が最大になるのは、顕熱は3~5月に300W/m2前後、潜熱は7~8月に400~500W/m2
前後であり、ボーエン比の気温・季節変化が明瞭である。
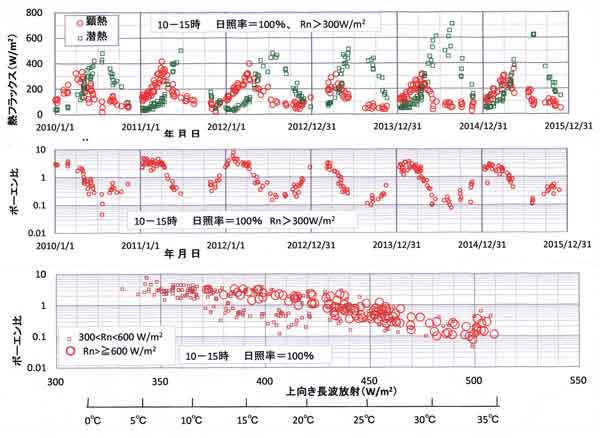
図123.9 晴天の日中平均(10~15時の日照率=100%、正味放射量Rn>300W/m2)の
熱収支量の季節変化(2010年~2015年の6年間)。
上:顕熱・潜熱輸送量の季節変化
中:ボーエン比の季節変化
下:ボーエン比の気温依存性
中図では、ボーエン比 Boの季節変化が明瞭に現れており、1~3月にBo=2~3程度であるのに対し、
5月以後はBo=0.1~0.2である。
図123.9の下図には横軸に樹冠上で観測した上向き長波放射量を選び、縦軸にボーエン比をプロット
してある。大きい丸印は、快晴に近い日射量の強い日中の正味放射量>600W/m2の場合で
ある。
上向き長波放射量は、森林全体の温度を代表するパラメータである。横軸の下段には黒体放射量に
換算したときの気温(℃)の目盛を付けてある。ボーエン比は気温上昇とともに単調に減少している
ことがわかる。
本研究によって乱流フラックスの観測データが解析された。晴天日中の顕熱は3~5月に300W/m2
前後、7~9月は100W/m2の大きさがある。森林内の開空間や森林のすぐ風下では、
この顕熱によって大気は加熱されることになる。7~9月よりも3~5月が加熱作用は大きいことが
定量的にわかる。このことから、森林内の開空間における日だまり効果による気温上昇量が、
特に春に大きくなる理由が理解できた(「K115.新宿御苑の気温分布(2)」
の図115.3参照)。
(c)日中の熱フラックスと風速の関係
ボーエン比は、気温のほか風速(正しくは交換速度ChU)にも依存する。
日中平均(10-15時)の顕熱・潜熱輸送量と風速との関係を調べる。ただし、風速は広域を代表する
測風塔の地上高度35mの北の丸公園の観測値を用いる。
図123.10のプロットは晴天時における顕熱(赤印)と潜熱(緑印)の観測値である。主に盛夏の
高温(Tr=25~35℃、Rn>650W/m2)、中間温(Tr=15~25℃、Rn>550W/m2)、
低温(Tr=3~15℃、Rn>450W/m2)の条件ごとに区分して示してある。
次の特徴がある。
(1)高温条件では潜熱が顕熱よりも大きいが、低温条件では逆転している。
(2)潜熱は風速とともに増加傾向であるが、顕熱は風速依存性が弱い。
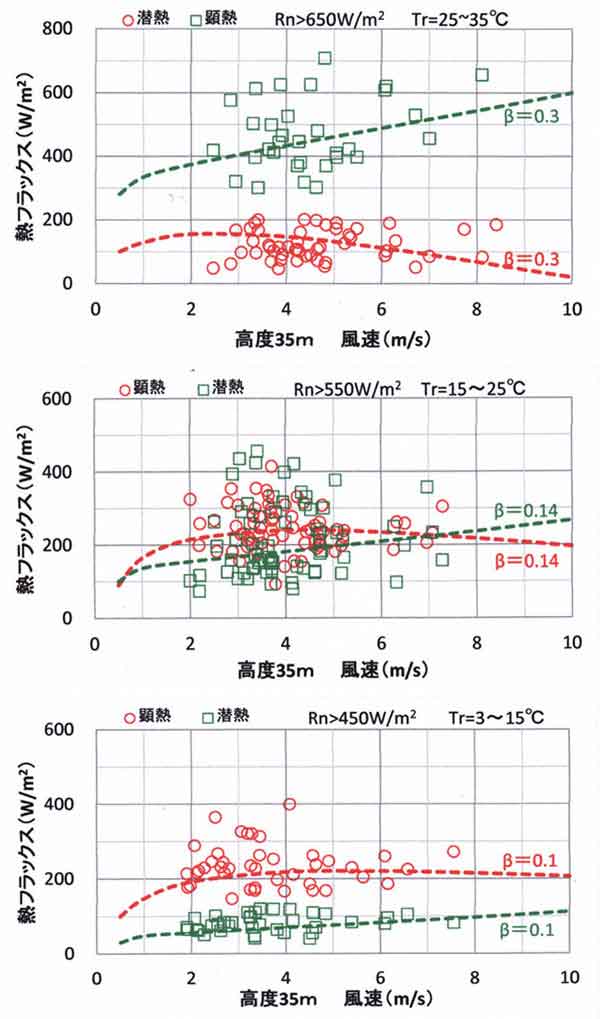
図123.10 晴天日中(10-15時、日照率=100%)平均の顕熱・潜熱と風速(北の丸:測風塔
高度=35m)の関係。破線は理論計算値。プロットは観測値で次の条件である。
上:Tr=25~35℃、Rn>650W/m2
中:Tr=15~25℃、Rn>550W/m2
下:Tr=3~15℃、Rn>450W/m2
次に、熱収支の理論計算によって検討してみよう。計算に必要な条件と観測値の平均値を表123.5に
まとめた。バルク係数Ch と蒸発効率βは観測値に最も適合する値を表に示してある。
理論計算では熱収支式、顕熱のバルク表示式、潜熱のバルク表示式の3式を解く(「水環境の気象学」
の6章、図6.3参照)。条件の広い範囲を計算するため、近似式(6.33~6.35)は使えないので、
逐次近似の解法を用いる(「地表面に近い大気の科学」の付録Fのプログラムを応用、部分的に
変更する)。
熱収支式を解く方法、その2
ー 温度差δT を意識しない場合 ー
熱収支法を用いる場合に必要な条件は、
有効エネルギー Q(=入力放射量-G)、G は樹冠葉面層から下向きの顕熱輸送量、
および気温、蒸気圧、風速(または交換速度)である。
計算結果として得られる要素(出力)は、
顕熱輸送量 H と潜熱輸送量 lE と樹冠層の有効温度の3つである。
この方法は、通常、バルク係数(または交換速度)と蒸発効率が既知の場合に利用されるが、
ここでは、蒸発効率βをパラメータとして変えて計算し、計算値(H と lE)が観測値(H と lE)
に最適合するβを求めようとしている。
特徴は、123.4節の「蒸発効率と交換速度」で用いた「その1」と異なる方法によってβを求める
のであり、樹冠層の有効温度の曖昧さを含んでいない。しかし、この方法でも有効エネルギーと
顕熱・潜熱の観測値に多少とも誤差を含むので、それらに最適合するβが求められる。
観測の誤差について検討した例が付録7の最後に「注意」として説明されている。
|
図中の破線は理論計算の結果である。パラメータは蒸発効率βである。
今回の観測値に適合する蒸発効率βは高温条件ではβ=0.30
(気温=30℃)、低温条件ではβ=0.10(気温=10℃)となり、以前の「1988年計算値」に利用した
8月のβ=0.26より大きく、2月のβ=0.10(気温=5~7℃)より小さい(あとの図123.12も参照)。
この傾向は「はしがき」の図123.1から予想されたことでもある。
今回の観測値に適合するバルク係数として、
Ch=0.005 ・・・・・・・ (8)
として得られた。この値は、「1988年計算値」に用いたCh=0.01より小さい。また、各地森林における
水文データの解析から得られた前記のCh=0.008~0.011よりも小さい。
その理由として考えられるのは、解析データは風速が1.9~8.4m/sの広い範囲に及び、特に強風時の
顕熱・潜熱観測値に計算値を合致させる必要があったからである。強風時の顕熱観測値を無視する
ならば、Ch>0.005を用いたほうが観測値に適合する。
このことから、Chは風速依存性があり、強風時ほど小さくなることが予想される。あとの123.7節に
おいて、Chの風速依存性が明らかになる。
表123.5 晴天日中(10-15時平均)における観測値の一覧表。
入力放射量 R↓=S↓-S↑+L↓
下層への熱 G=(S↓-S↑+L↓-L↑)-(H+lE)=Rn-(H+lE)
有効エネルギー Q=R↓-G
“観測”:観測値
“計算”:熱収支式を解く計算に用いる条件(Chとβは観測全体に最適合する値)
観測範囲 35℃>Tr>25℃ 25≧Tr>15℃ 15≧Tr>3℃
入力放射量 R↓ W/m2 1166±34 1046±41 909±66
下層への熱 G W/m2 85±75 159±78 222±51
有効エネルギーQ 観測 W/m2 1081 887 687
Q 計算 W/m2 1100 900 700
実効温度Tr 観測 ℃ 30.9±3.0 21.0±2.8 11.2±2.5
Tr 計算 ℃ 30 20 10
蒸気圧 Vp 観測 hPa 22.4±7.7 8.0±3.4 3.4±1.1
Vp(湿度) 計算 hPa 21.3(50%) 8.2(35%) 3.7(30%)
バルク係数 Ch 計算 0.005 0.005 0.005
蒸発係数 β 計算 0.30 0.14 0.10
風速(北の丸) m/s 4.6±1.3 4.0±1.1 3.7±1.4
風速(教育園) m/s 2.4±0.8 2.2±0.8 2.4±1.0
露場気温(大手町*)℃ 30.5±3.6 19.5±3.1 10.0±2.2
顕熱 H 平均 W/m2 122 246 234
潜熱 lE 平均 W/m2 470 216 82
全観測個数 50 69 43
顕熱観測個数 50 69 43
潜熱観測個数 32 69 37
*2014年12月2日以後は北の丸露場における観測
123.6 バルク係数と蒸発効率の風速依存性
強風・微風条件における植物の反応として次のことが考えられる。
(1)葉面は強風時に裏返し状態になりアルベドが大きくなる可能性がある。
(2)強風時に葉面が振動し顕熱交換のバルク係数が変化する可能性がある。
(3)晴天日中の微風時は大気の不安定度が大きくなることでバルク係数は変わる。
(4)乾燥・強風時は過大蒸散を防ぐために気孔を閉じ、蒸散を少なくしようとする。
これらのことから強風時には蒸発効率が小さくなる可能性もある。その状態では、潜熱の減少に
ともなって葉面温度は異常高温となり、顕熱が増加する。
気象条件が揃ったデータに対して熱収支式を解き、観測値と比較する。
10-15時の晴天(日照率=100%)日の実効温度Trとして30~35℃、正味放射量Rn>650 W/m2
の条件を選び出し、顕熱H、潜熱lEのいずれかのデータ無しの場合は除く。
(1)を検討するために、図123.11にアルベドと風速の関係を示した。風速=3~9 m/sの範囲で
プロットのばらつきもあるが、風速の増加にしたがってアルベドが上昇する傾向にあるようにも見えるが、
アルベドの風速依存性は明確には認められない。
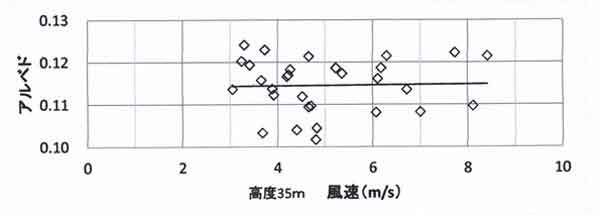
図123.11 アルベドと風速の関係。プロットは観測値、実線は最小自乗法で描いた関係。
次に(2)~(4)について検討する。観測値に適合するバルク係数 Ch と蒸発効率βを見いだす
ために熱収支の理論的な計算を行う。
計算条件は観測値に基づき、
入力放射量 R↓=1185W/m2、樹冠層から下向きの顕熱輸送量G=54 W/m2、
有効入力エネルギー Q=R↓-G=1131 W/m2、気温 T=32.8℃、蒸気圧 Vp=27.2hPa
(相対湿度=54.7%)である。
現実の乾燥・高温条件では、強風時の風速増加に対してバルク係数は変化し、同時に蒸発効率も
減少すると考えられる。しかし、観測誤差を多少とも含む顕熱・潜熱の観測値を用いる場合、
高温時においてβの風速依存性およびバルク係数 Chの風速依存性を同時に得ることは難しい。
それゆえ、この節では、β=一定と仮定した場合のChの風速依存性と、ChUの風速依存性を与えた
場合のβの風速依存性を検討する。
(d) バルク係数の風速依存性
βは一定値として与えた場合について、ChUの風速依存性をもとめる。盛夏の蒸発効率としてすでに
得られているβ=0.30を用いる。
図123.12(上)は風速と顕熱・潜熱の関係である。プロットは観測値、実線は計算値である。
風速U=4.2m/sおよび6.5m/sの周辺でプロット数が多い位置で観測値と計算値がほぼ一致している。
それゆえ、それら風速におけるバルク係数は次のように決めることができる。
風速=3~7m/s の範囲:
Ch=0.008 ・・・ 風速≒4.2m/s前後
Ch=0.004 ・・・ 風速≒6.5m/s前後
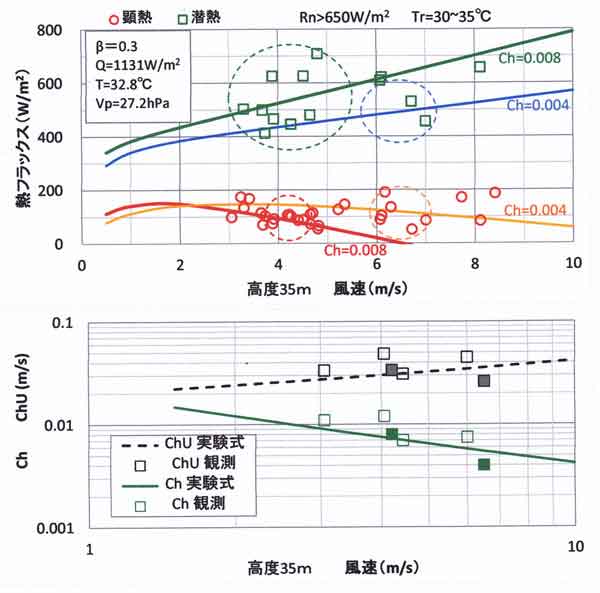
図123.12 バルク係数の風速依存性をもとめる図。
上:バルク係数Chをパラメータとしたときの顕熱・潜熱と風速(高度35m)の関係。
プロットは観測値、実線は計算値(Ch=0.004、0.008)。
破線の大きい丸はプロット数の多い U=4.2m/sおよび6.5m/sの条件について、計算値と観測値が
ほぼ一致しているとみなして ChをそれぞれCh=0.008、および0.004として決めた。
下:交換速度ChUおよびバルク係数Chと風速の関係、両対数目盛で表してある。
下方の緑四角印はバルク係数、緑実線はChと風速の関係を表す実験式
上方の黒四角印は緑四角印を基に計算した交換速度ChU
黒破線は緑実線を基にした交換速度ChUの実験式
Ch=0.008とCh=0.004の値は図123.12(下)に緑塗り印で示した。白抜き緑印は、前記の123.4節
「蒸発効率と交換係数」で、連続晴天日の観測から決めた値である(表123.3)。
交換速度と風速の関係を表す実験式をどう決めるか?
ばらついたデータから、交換速度 ChU と風速 U の関係をどのような実験式で表すか、理論的考察が
必要となる。
まず、潜熱輸送量と風速の関係を示す観測値のプロット全体をみると、潜熱輸送量は風速とともに
増加傾向にある(図123.12上に類似する図123.10、および付図4)。熱収支理論によれば、
この傾向は交換速度ChUが風速の増加に対して大きくなることを意味する(「水環境の気象学」の図6.3)。
次に ChU の関数形について考察する。森林の樹冠層は0.1m前後の葉面の集合体からなる。
有限大の物体に対するヌッセル数 N の定義は次式で表される。
N=比例係数×ChU
レイノルズ数=0.1~104の範囲にある小物体の N は、
N=a+b×U1/2
の形式で表現される(「大気境界層の科学」のp.71~p.73)。
こうした理論と矛盾しないようにChUの実験式を決めなければならない。Chのプロットに緑実線を
あてはめると、ChU の実験式(黒破線)は次のようになる。
ga=ChU=0.01 + 0.01× U1/2・・・・・ (9)
U=1~10m/sの範囲では、
ga=ChU=0.020~0.042m/s
となる。ここに、U は高度35mの風速である。
なお、高度50mの地域代表風速 UBを利用する場合でも、式(10)を用いてよい(備考2)。
注意
式(9)で表した交換速度 ChU は晴天日中の観測値に基づいたものであり、微風時にゼロにはならない。
それは、微風時の葉面群(樹冠層)の温度が上昇し、自由対流によって顕熱輸送が生じるからである。
葉面群の温度が気温に比べて低くなる夜間の微風時の ChU はここで求めた値より小さくなる。
(e) 蒸発効率の風速依存性
図123.13の緑と赤の実線は、交換速度ChUの実験式(9)を与えたときの、風速と顕熱・潜熱の関係
である。蒸発効率βをパラメータとして表してある。
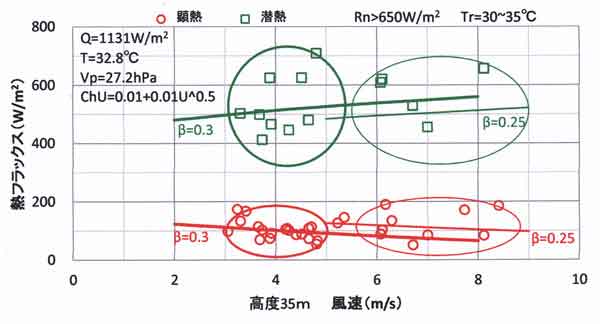
図123.13 顕熱・潜熱と風速の関係、プロットは観測値。
実線はChUを与え、蒸発効率β(0.03、0.025)をパラメータとして表したときの顕熱・潜熱と風速の
関係。
大きい丸で囲む範囲内のプロットが計算値と一致するとみなせるならば、風速=4m/s前後ではβ=0.3、
風速=7m/s前後ではβ=0.25前後となる。βは風速の増加とともに小さくなる傾向に見えるが、
プロットのばらつき(観測誤差)もあり明確ではない。
すなわち、潜熱について詳しくみると、緑実線で表すβ=0.3の計算値は風速 9 m/s の範囲まで延ばし
てもよい。しかし、顕熱については、風速=5~8m/sの範囲はβ=0.25の赤実線で表す計算値の
ほうが一致している。これら両方を考慮すると、βが強風時に小さくなるとは断言できない。
備考5:風速依存性の正しい評価方法
本研究では、樹冠層の実効温度 Te の真値および樹冠の上の正確な気温 T を観測していない。
そのため、熱収支式と顕熱・潜熱のバルク式の3つの式から交換速度ChU(または
バルク係数Ch)の風速依存性、および蒸発効率βの風速依存性を正確に知ることは原理的に
難しい。より正確に求めるには、正しいδT=Te-T の観測も必要である。
123.6 蒸発効率の着葉前後での違い、蒸発効率の季節変化
この節では、前節で最終的に得られた交換速度と風速の関係式(9)を与えたとき、
計算値と観測値が適合する蒸発効率βをもとめる。
(f)着葉前後の蒸発効率
蒸発効率は着葉の状態(葉面積指数)に依存すると考えられる。
自然教育園の森林では、4月下旬~5月中旬の期間に着葉が急激に進み、常緑樹林と落葉樹林での
気温差、あるいは林内開空間と大手町露場の気温差が急激に変わる
(「K107.林内気温の日変化・季節変化、春~入梅期」の107.4、
図107.5を参照)。
この気温差にみられる急変は、着葉による熱収支条件の急変に対応する。これを蒸発効率の変化からみること
にしよう。
2010~2015年の6年間のデータから日中10-15時の晴天条件(日照率=100%、
正味放射量Rn>550W/m2)を選び出す。
4月15日以前を着葉前、5月5日以後を着葉後とする。ボーエン比は気温依存性が強いので、
選び出した晴天条件から、さらに着葉の前後で気温がほとんど同じ条件(Tr=22.0~23.5℃範囲)の日を
選ぶ。着葉前は5日間(4月9日を中心、平均気温=22.9℃)、着葉後は7日間(5月24日を中心、
平均気温=22.7℃)である。その他の観測・計算条件などは付録7の付表3に示した。
熱フラックスの観測値と風速の関係を図123.14にプロットで示した。図中の破線は計算値と観測値が適合する
蒸発効率βを用いたときの計算結果である。
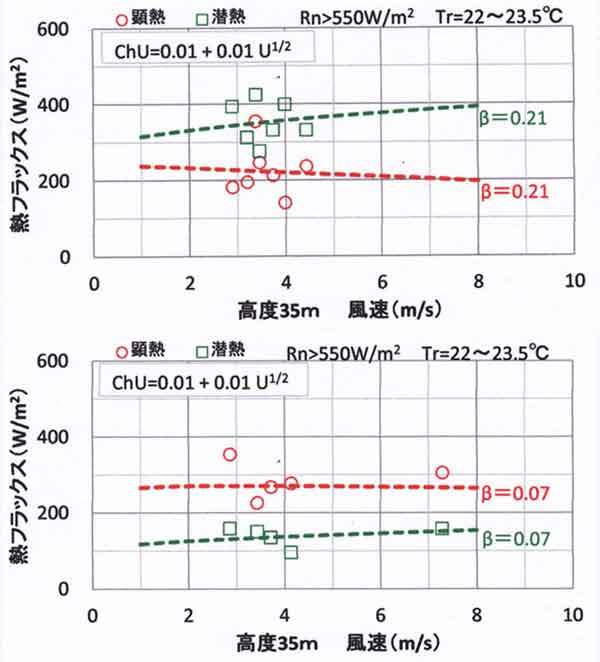
図123.14 晴天日中(10-15時、日照率=100%)の条件における平均の顕熱・潜熱輸送量と風速
(北の丸:測風塔高度=35m)の関係。破線は理論計算値。プロットは観測値である。
上:着葉後:Tr=22.7℃(22~23.5℃)、Rn>550W/m2
下:着葉前:Tr=22.9℃(22~23.5℃)、Rn>550W/m2
付録6に示した補足計算も含め、蒸発効率と気温の関係を次項の図123.12に示した。
(g)蒸発効率の季節変化
前項の計算と同様に、式(9)で表される交換速度を与えたときの計算値と観測値が適合する蒸発効率βを
月ごとにもとめる。
6年間(2010-2015年)の日中10-15時の晴天条件(日照率=100%、正味放射量Rn>300W/m2)
で、かつ有効な顕熱データのある日(336日間)を選び出す。そのうち潜熱データの得られた日数は
293日間である。
これまでに示した図からわかるように、顕熱は風速=2~6m/sの範囲で風速依存性が弱い。そこで条件
をしぼり、風速=2~6m/sの範囲で顕熱も潜熱も得られている日を選ぶと250日間となる。
計算に必要な条件と計算結果は付録8に示した。計算結果は図123.15に示した。
上図の中に付記した数値は月番号を示す。蒸発効率と気温の関係は、反時計まわりのループ状に結ばれる。
4月から6月にかけてと、9月から12月に急変することがわかる。前者は新緑、後者は落葉の季節に対応している。
下図は蒸発効率の季節変化であり、「1988年計算値」に用いた蒸発効率は破線で示し、緑線は
今回の資料解析から得られた蒸発効率の季節変化を見やすくしたものである。横軸の例えば
「4月」目盛の位置は4月15日と見てよく、4月末~5月15日ころ、蒸発効率が急上昇する。
新緑が目立って鮮やかになる季節に対応する。
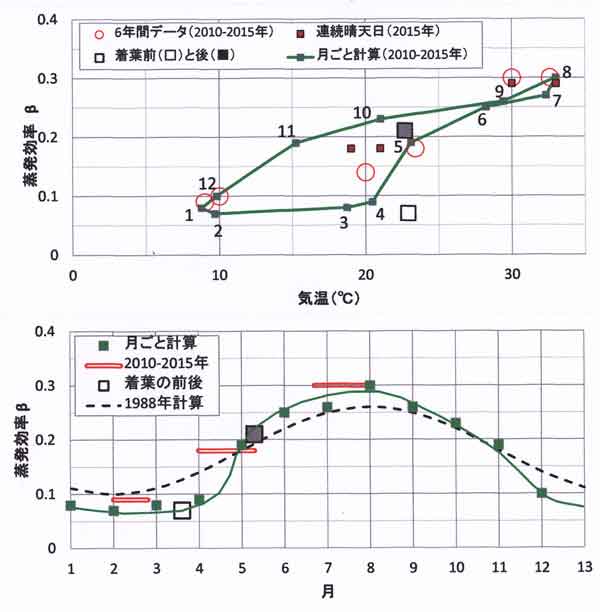
図123.15 蒸発効率と気温の関係(上)、および季節変化(下)。
上図の記号
数字1、2、・・:1月、2月、・・を表し、順番に緑線で結合
赤丸印:2010-2015年の晴天日の計算(図123.10と付図2に基づく)
大きい四角印:着葉前(白抜き)と着葉後(黒塗つぶし)
小さい四角印:2015年の8月と10月の連続晴天日(表123.3)
下図の記号
破線:「1988年計算値」に用いた蒸発効率
横赤線:気温がほぼ揃った条件について求めた蒸発効率(上図の赤丸)
四角印:着葉前と着葉後
以上の結果から、蒸発効率は気温とともに大きくなる傾向にあるが、着葉(葉面積指数)の状態に
敏感に反応することがわかった。
123.8 まとめ
東京白金台の森林公園「自然教育園」の樹冠上で6年半にわたり観測した熱フラックスを解析した。
それらは顕熱・潜熱輸送量の乱流フラックスと、長波・短波の下向き・上向きの放射フラックス
の6要素である。
(1)顕熱と潜熱の関係
晴天日中の熱輸送量が最大になるのは、顕熱は3~5月に300W/m2前後、潜熱は7~8月に400~
500W/m2前後である。これはボーエン比の気温依存性によるものである。ボーエン比の
季節変化・気温依存性が明瞭に現れた。
晴天日中のボーエン比Boについて、1~3月にはBo=2~3程度であるのに対し、5月から夏にかけて
Bo=0.1~0.2となり、秋から冬に向かって再び増加していく(図123.9)。
(2)年蒸発散量
欠測日を含めた潜熱輸送量の平均値として73W/m2(年蒸発散量=940mm/y)が得られた。
この値が各地森林の水文データや、熱収支計算から得られている「1988年計算値」に比べて
10%程度大きいのは、乱流フラクスの観測は降雨日に欠測が多いこと、東京都心部の近年の都市化による
温暖・乾燥化による影響が考えられる。10%のうちの5%は、敏感度テストから、都市温暖・乾燥化
(この25年間の東京の都市化による0.5℃の気温上昇と3%の湿度減少)の影響によるものである。
(3)アルベド
全期間のアルベドの平均値=0.116である。夏期晴天日について調べると、アルベドは風速の増加とともに
大きくなるようにもみえるが、明確な風速依存性は見出せない(図123.11)。
(4)バルク係数と交換速度
高度35mの風速(気象庁北の丸公園測風塔)を用いたときの森林の顕熱輸送のバルク係数として
Ch=0.004~0.012(風速=2~8m/sの範囲)が得られた。その結果として、交換速度は、
ga=ChU=0.020~0.042m/sである(図123.14、式9)。
(5)蒸発効率
晴天日中(10-15時)における蒸発効率として、冬期のβ=0.07~0.09から盛夏のβ=0.30
(気温30℃前後)を得た。森林の蒸発効率は気温のほか、着葉状態(葉面積指数)に大きく依存する
(図123.15)。すなわち、新緑の4月末から5月中旬にかけて、0.1程度から0.25に急激に上昇し
盛夏に0.3程度に達し、その後、落葉とともに(気温の低下とともに)0.1程度に下降していく。
強風時における蒸発効率は風速の増加にしたがって小さくなるか否か、風速(測風塔高度=35m)が
9m/s以下の範囲内では、明確な風速依存性は見出せない。
今後の課題として、
(6)高精度の気温観測を行うこと
自然教育園の樹冠上と大手町露場の温度差は3~5月に+1~+2℃と大きくなることがわかった。
3~5月は樹冠上の顕熱輸送量が最大になる季節である。本観測では、2015年6~10月の期間は高精度通風筒を
用いた気温計で観測したが、それ以外の期間の気温観測は強制通風式装置で行ったが放射誤差を含む。
それゆえ、樹冠上の代表気温として上向き長波放射計の放射量観測値から換算した実効温度Tr で代表したため、
±1℃程度の誤差が見込まれる。それゆえ、今後、樹冠上で観測した高精度気温計による気温から、
上記の気温差(付図3)を確認したい。
同時に、樹冠層からの顕熱・潜熱輸送量をバルク式で表すときの実効温度 Teの観測も行なう。熱収支式に
よるTe, H, lEの3要素の計算値と、観測値の比較によって、交換速度ChU(またはバルク係数Ch)の風速依存性と、
強風時における蒸発効率βの風速依存性をより正しく求めたい。
(7)微風時および夜間の交換速度
交換速度 ChU の関数形を正確に決めるためには、微風時の解析が必要である。
本報告では、晴天日中について解析したが、今後は潜熱が小さくなる夜間の顕熱輸送量の観測値にも注目して
解析を行ない、ChU の関数形を確定したい。
微風の夜間には、安定度の影響によりChUは晴天日中に求めた値に比べて小さくなることに注意し
よう。
(8)ボーエン比の気温依存性について他の地表面との比較
本研究により、森林におけるボーエン比 Boの季節変化が定量的にわかった。この結果と他の地表面に対する
関係を比較し、蒸発効率や他の条件との関係を明らかにしたい。
(9)降雨時の濡れた樹体からの遮断蒸発量
降雨時について観測データの品質管理を再度行い、確かなデータから降雨時の遮断蒸発量と風速や
入力放射量などとの関係を評価し、水文資料に基づく結果や計算モデル(近藤・石井、1992;
近藤・渡辺・中園・石井、1992;近藤・中園・渡辺、1992)と比較・検討する。
(10)欠測時の顕熱・潜熱輸送量の補完
欠測時の顕熱・潜熱輸送量として熱収支式を解いて補完し、年間の蒸発散量を
評価する。計算方法は、付録9に示されている。
付録1 従来の水収支法とフラックスの直接測定法による熱収支量の違い
(1)蒸発効率は「1988年計算値」に用いた値よりも夏は大きく冬は小さい
熱収支量の「1988年計算値」は、モデル森林に対する値であるのに対し、観測値は風速・気温・湿度
の乱流変動の観測による「直接測定値」である。
モデル森林として葉面積指数、降雨時の葉面の貯水量、蒸発効率の季節変化を与えている。
熱交換のバルク係数は一定値のCh=0.01を用い、降水時の蒸発効率β=1、無降水日の蒸発
効率β=0.10(2月)~0.26(8月)をもつように波数1の単純な正弦関数の季節変化を与えている。
ただし、気象要素は日々の実測値を用いてある。
このモデル森林に対する計算値は各地試験流域(東山、桐生、川向、去川2号沢、竜の口北谷)
における水収支法による結果とよく一致するように決められたものである(近藤・中園・渡辺・桑形、
1992)。
(2)東京の高温・乾燥化による蒸発散量の増加
大都市・東京の特徴として近年は都市化による高温・乾燥化が進み、「1988年計算値」に比べて
最近の2010年以後は蒸発散量が増える可能性がある。
東京の年平均水蒸気圧は1960年(13.78hPa)を基準とすると2000年時点で0.41hPa(相対湿度は7%)
減少している、ただし5年移動平均の平滑化した値での比較である(近藤、2012)。
付図1は東京における相対湿度の経年変化である。ただし、観測露場は2014年12月2日に大手町から
北の丸に移転し、湿度の年平均値は6.5%、寒候期(1、2、3、12月)は7.6%、暖候期(6~9月)は
7.6%、それぞれ高くなったので、2015年は元の大手町露場における値に換算した値をプロット
してある(「K54.日だまり効果と気温:東京新露場」)。
湿度の観測方法は時代によって異なるので、図示された値は真値と多少の違いはあるが、大都市ほど
乾燥化が進む傾向にあることは間違いない(近藤、2012)。
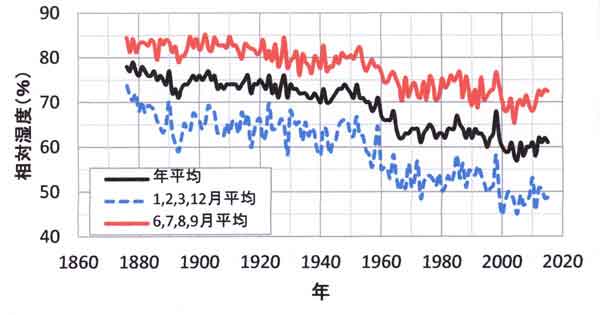
付図1 東京における相対湿度の経年変化。
露場は2014年12月2日に大手町から北の丸に移転され湿度は高くなったので、2015年は元の大手町
露場における値に換算した値をプロットしてある。
付図1によれば、1960年以後の年平均湿度は、1年当たり0.1%の割合で減少している。この割合を
1988年から2013年までの25年間に換算すると2.5%の乾燥化となる。あるいは、1986~1990年の5年間
平均湿度に比べて2011~2015年は2.6%減少している。この乾燥化によって、今回の潜熱輸送量
(蒸発散量)の観測値は大きくなる可能性がある。
付録4の敏感度テストによれば、最近25年間の高温・乾燥化により都心部の森林における蒸散量は
5%程度増加する。
付録2 日中のデータの品質管理(10-15時平均データ)
本文で説明したように、本解析では、30分ごとにまとめられた乱流フラックスと放射フラックスの
平均データをもとに解析している。日平均値は30分ごと48個のデータの平均値であり、48個中に
欠測(データなし)が1~2個あっても大きな誤差は生じないが、日中の10-15時平均値は30分データ
の10個の平均値であるため、品質管理を別途行う必要がある。
樹冠面における熱収支量の残差は樹冠面から下層へ向かう顕熱輸送量G(下層への熱)である。
それを示した図123.3(上)によれば、2009年の後半期間と、それ以後の期間で違いが見られる。
そのため、日中(10-15時)の平均値に関して2009年は徐外し2010~2015年の6年間について
解析する。
また、日平均値については、123.3節「観測データの品質管理(日平均データ)」で述べたように、
日降水量>10mmの日の日平均値の乱流フラックス(顕熱、潜熱)、及び下向き長波放射量は除去し、
データ無しとしたが、日中(10-15時)の平均値については、明らかな誤信号と認められる場合以外は
降雨時も有効データとして用いる。
日射量(下向き短波放射量)については、すでに落雷による器械損傷前(2013年7月22日以前)
は10%小さく補正してある。
付図2の上図は日中平均の樹冠面から下層への熱輸送量 G の6年間の季節変化である。年々の違いは
あり、観測誤差とみなされる部分もあるが、全期間を通して大きな誤差はなしとしておこう。
中図は北の丸公園の日射量に対する自然教育園の日射量の比である。
両地点間の距離は6.6kmあり、天空条件を揃えるために日照率=100%の条件のみをプロットして
ある。日射量の比は、年によって季節変化して日射計の傾斜による誤差を含む可能性があるが、
全期間として日射量の比は0.99であるので、大きな誤差はなしとしておこう。
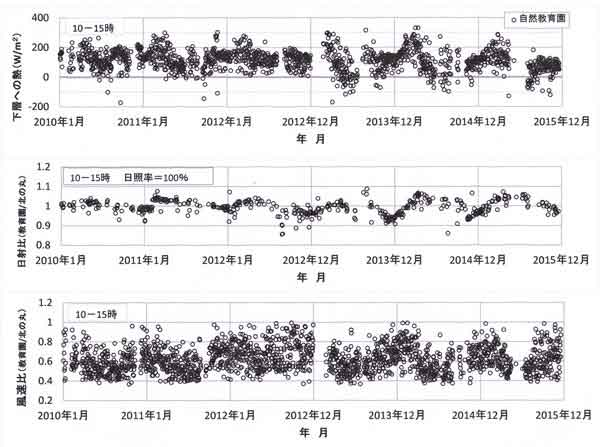
付図2 日中(10-15時)の平均量の季節変化(2010年1月~2015年12月の6年間)。
上:樹冠上で観測した熱収支量の残差(樹冠面から下層への顕熱フラックス)
中:北の丸公園の日射量に対する自然教育園の日射量の比
下:北の丸公園の風速(高度35m)に対する自然教育園の風速(高度20m)の比
下図は北の丸公園の風速(気象庁測風塔の地上高度=35m)に対する自然教育園の風速(地上高度
=30m)の比である。風速の比が極端に大きい日、または極端に小さい日の風速は誤信号を含むほか、
大気条件が両地点で大きく異なる場合であり、この日中はデータなしとした。
その理由は、森林の蒸発効率を評価する際に、東京都心部を代表する測風塔地上高の高い北の丸公園の
風速を用いるので、両地点の大気条件が大きく異なる日は解析データに含めない。
下図には、解析に選んだ日中平均値がプロットされていて、風速比=0.37~0.99の間に入っている。
なお、全期間6年間の風速比の平均値=0.63である。
付録3 上向き放射量で定義する樹冠の実効温度 Tr と露場気温の関係
観測塔の周辺は比較的密な森林であるが、完全に密でないために樹冠の上で観測される上向き
長波放射量には、樹冠代表温度のほか林床までの下層の低温度からの長波放射量も一部含まれる。
この放射量を黒体温度に換算した温度 Tr を樹冠の実効温度を呼ぶことにする。樹冠上の気温と Tr の差
は±2℃以内にあり、近似的に等しい。したがって、Tr は概略的に森林上部層を代表する
気温とみなすことができる。
樹冠上では、気温は通風式気温計で観測されたが、2015年5月~10月の期間、高精度の通風式気温計と
比べると、晴天日中は放射の影響により1~2℃ほど高めに観測される(「K117.自然教育園の林内
気温」の図117.9)。それゆえ、熱収支解析を行うには精度が不十分である。そのかわりに、
Tr を林内から樹冠の上の大気層までを代表する気温として用いることにする。
付図3は日中(10-15時)平均のTr と大手町露場の気温の差について6年間にわたる季節変化である。
温度差は0.5±1.0℃である。ここに晴天時とは、10-15時の日照率=100%で正味放射量
Rn>300W/m2 の条件とする。
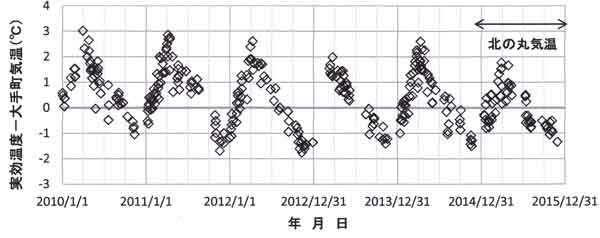
付図3 晴天日中(10-15時、日照率=100%、正味放射量Rn>300W/m2)における実効温度 Tr と
大手町露場の気温との差の季節変化(2010年1月~2015年12月の6年間)、ただし、2014年12月2日
以後は、北の丸露場における気温との差である。ここに、Trは樹冠上で観測した上向き長波放射量
を黒体温度に換算した温度である。
図に示された顕著な特徴として、大手町露場と自然教育園の樹冠上の温度差は3~5月に+1~+2℃と
大きくなっている。図123.9に示したように、3-5月は樹冠上の顕熱輸送量が最大になる季節である。
注意として、付録5で示すように長波放射計の誤差6 W/m2は、Tr の誤差1℃に相当する。
今後、樹冠上で高精度気温計を用いて気温を観測し、付図3を確認する必要がある。
付録4 熱収支量の敏感度テスト
気温、湿度などの気候変化や観測誤差(測器の誤差と代表性の誤差)に対する顕熱輸送量 H と
潜熱輸送量 lE の敏感度テストを行う。代表条件として付表1の条件を
与える。この条件は大雨日(遮断蒸発量のみ)を除いた条件を想定したものである。
(1)~(5)の条件について理論的な熱収支計算の結果を表の下段の3行に示した。
条件(1)を基準としたときの、顕熱・潜熱輸送量の変化割合を%で示した。条件(3)は
東京都心部の近年25年間の温暖・乾燥化によって気温が0.5℃上昇、相対湿度が3%減少した場合に
相当する。
付表1 顕熱・潜熱輸送量の敏感度テスト。
風速U(高度=35m)=4m/s、バルク係数Ch=0.008(ChU=0.032m/s)とする。
Q=R↓-G:有効エネルギー
R↓=(S↓-S↑+L↓):入力放射量
G:樹冠面から下層への熱フラックス(理論的に、日平均値・年平均値はゼロに近い)
β:蒸発効率
(1) (2) (3) (4) (5)
基準 乾燥化 温暖・乾燥化 Qの増加 βの誤差
気温 ℃ 20.0 20.0 20.5 20.0 20.0
相対湿度 % 50 47 47 50 50
蒸気圧 hPa 11.69 10.98 11.33 11.69 11.69
Q W/m2 500 500 500 525 500
β 0.2 0.2 0.2 0.2 0.22
H W/m2 -36.8 -42.2 -46.3 21.0 -44.4
lE W/m2 132.3 129.5 131.5 130.2 132.0
lEの変化 % 0.0 +5.0 +6.7 +5.6 +7.1
敏感度テストによれば、相対湿度3%、気温0.5℃、有効エネルギー(入力放射量)5%の変化、
あるいは蒸発効率βの0.02の誤差によって、潜熱輸送量(蒸散量)が5~7%程度変化することがわかる。
付録5 放射量の観測誤差6 W/m2は実効温度Trの誤差1℃に相当
123.4節「蒸発効率と交換係数」では、日平均値の計算では、樹冠の葉面温度(樹冠代表温度)Tsが
上向き長波放射量L↑に相当する黒体温度Trに等しいとして蒸発効率と交換係数を評価した。
この場合、L↑=400~500W/m2について1.2~1.5%の誤差(6 W/m2 )
があれば、Trの誤差は1℃となる。高精度の放射計であっても2~3 W/m2程度の誤差は
含まれる。それゆえ、123.4節「蒸発効率と交換係数」の方法による蒸発効率と交換係数の評価は
非常に難しいことがわかる。
放射計がもつ誤差の目安をみるために、日射計による晴天夜間の値をしらべてみる。下向き日射計
では-1.5 W/m2(8月)~-2.5 W/m2(10月)、上向き日射計では
+2.4 W/m2(8月)~+3.7(10月)W/m2と観測されている。他の多くの
一般の放射計でも同様である。
夜間はゼロであるはずの値がゼロにならないのは、放射計本体及びフィルターの温度が日中は気温
より高温に、夜間は低温になることによる。日中の誤差は夜間の誤差よりも大きくなる。
ほかに放射計の原理からくる避けがたい誤差もある。普通の放射計では10 W/m2程度の
誤差がある(「水環境の気象学」の4.8節;「大気境界層の科学」の2章の(3)放射計)。
10 W/m2程度の誤差は、123.3節「観測データの品質管理」で調べた誤差と同じである。
付録6 日中の熱フラックスと風速の関係(補足資料)
123(c)節では、顕熱・潜熱フラックスを実効温度の3つの範囲(35>Tr>25℃、25≧Tr>15℃、
15≧Tr>3℃)に分けて解析した。それを補足するために、温度のより狭い3範囲についても同様の
解析を行う。その条件を付表2に示し、理論計算から蒸発効率をもとめた。
付図4は晴天日中(10-15時、日照率=100%)平均の顕熱・潜熱フラックスと風速の関係である。
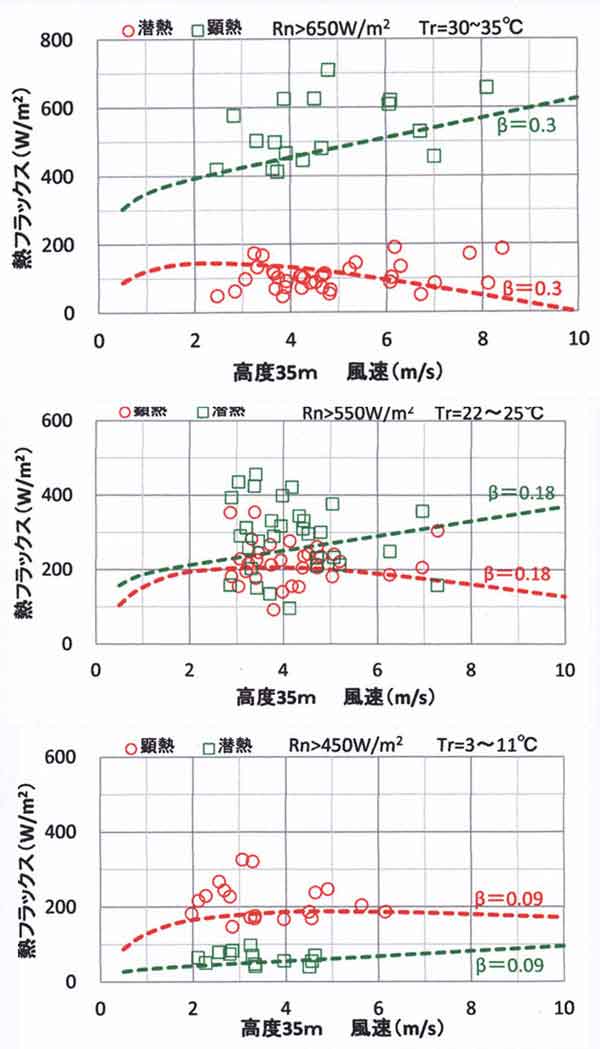
付図4 晴天日中(10-15時、日照率=100%)の顕熱・潜熱フラックスと風速の関係。
上:Tr=30~35℃、Rn>650W/m2
中:Tr=22~25℃、Rn>550W/m2
下:Tr=3~11℃、Rn>450W/m2
付表2 晴天日中(10-15時平均)における観測値の一覧表(表123.5の補足計算資料)。
入力放射量 R↓=S↓-S↑+L↓
下層への熱 G=(S↓-S↑+L↓-L↑)-(H+lE)=Rn-(H+lE)
有効エネルギー Q=R↓-G
“観測”:観測値
“計算”:熱収支式を解く理論計算に用いる条件(Chとβは観測値に最適合する値)
観測範囲 35℃>Tr>30℃ 25≧Tr>22℃ 11≧Tr>3℃
入力放射量 R↓ W/m2 1183±24 1067±37 867±52
下層への熱 G W/m2 62±87 119±73 227±40
有効エネルギーQ 観測 W/m2 1120 948 640
Q 計算 W/m2 1120 950 640
実効温度Tr 観測 ℃ 32.6±1.4 23.4±0.8 9.0±1.5
Tr 計算 ℃ 32.6 20.4 9.0
蒸気圧 Vp 観測 hPa 26.1±4.0 10.5±2.8 2.9±0.9
Vp(湿度) 計算 hPa 26.1(53%) 10.5(36%) 2.9(25%)
バルク係数 Ch 計算 0.005 0.005 0.005
蒸発係数 β 計算 0.30 0.18 0.09
風速(北の丸) m/s 4.7±1.5 4.2±1.1 3.6±1.2
風速(教育園) m/s 2.4±0.9 2.3±0.7 2.5±1.0
露場気温(大手町*)℃ 32.5±1.6 22.2±1.1 7.9±1.3
顕熱 H 平均 W/m2 122 246 234
潜熱 lE 平均 W/m2 470 216 82
全観測個数 36 32 19
顕熱観測個数 35 32 19
潜熱観測個数 17 32 13
*2014年12月2日以後は北の丸露場における観測
付録7 着葉の前・後の条件一覧表
自然教育園の森林は、4月中旬~5月中旬の期間に着葉が急激に進む。着葉前後の観測値と熱収支
計算に必要な気象要素を付表3に示した。計算はChUの式(9)を用いたときの結果。
付表3 着葉期の前・後の晴天日中(10-15時平均)における観測値。
観測範囲 着葉前 着葉後
3月31日~4月14日 5月5日~6月26日
(中心の日付) (4月9日) (5月24日)
入力放射量 R↓ W/m2 1042±15 1082±39
下層への熱 G W/m2 181±56 69±97
有効エネルギーQ 観測 W/m2 861 1013
Q 計算 W/m2 910 1050
実効温度Tr 観測 ℃ 22.9±0.5 22.7±0.9
Tr 計算 ℃ 22.9 22.7
蒸気圧 Vp 観測 hPa 8.7±1.9 9.5±2.8
Vp(湿度) 計算 hPa 8.7(31%) 9.5(34%)
蒸発係数 β 計算 0.07 0.21
風速(北の丸) m/s 4.3±1.7 3.6±0.5
風速(教育園) m/s 2.4±0.9 2.0±0.4
露場気温(大手町*)℃ 21.2±0.7 21.7±0.6
顕熱 H 観測 W/m2 286 224
顕熱 H 計算 W/m2 284 223
潜熱 lE 観測 W/m2 140 353
潜熱 lE 計算 W/m2 142 352
全観測個数 5 7
顕熱観測個数 5 7
潜熱観測個数 5 7
*2014年12月2日以後は北の丸露場における観測
注意:観測誤差(観測点の代表性の誤差)についての考察
表に示した下層への熱 G=181±56、及び69±97 W/m2の標準偏差(±56、±97 W/m2)
が大きいのは観測誤差も含まれている。それゆえ、この計算では有効エネルギーの観測値
Q(861、1013W/m2 )を 4~6% ほど替えた Q(910、1050W/m2 )を用いると、
顕熱 H と潜熱 lE の計算値が観測値とほとんど一致している。
風速や気温や蒸気圧を0.5m/s、0.5℃、0.5hPa程度替えて計算しても、似たような結果になる。
この結果は、放射と乱流フラックスの各項に10~20W/m2 程度の誤差が含まれていることを
意味している。他の表や図でも同様に、観測値をそのまま用いると、例えば H の計算値は観測値より
10W/m2 ほど過大となり、逆にlE の計算値は観測値より過小となっている。つまり、観測値
に誤差があると、熱収支式は閉じない。
「熱収支のインバランス」には、2つの意味があり、その1は観測誤差によるもの、その2は観測高度が高い
ときに見られる現象である。通常の観測では、その1の場合が多い。
データ解析に際して、丁寧な品質管理を行うことが重要である。
付録8 月ごとの日中10-15時の晴天条件
2010-2015年の日中10-15時の晴天条件について、月ごとに蒸発効率βを評価した。その条件と
計算結果を付表4に示した。
付表4 2010-2015年の日中10-15時の晴天時について計算する条件と計算結果
計算はChUの式(9)を用いたときの結果。
日照率=100%、正味放射量Rn>300W/m2
風速(気象庁丸の内公園内の測風塔高度35m)=2~6m/s
Rn:正味放射量(W/m2)
R↓:入力放射量(W/m2)
G:下層への熱(W/m2)
Q=R↓-G:有効エネルギー(W/m2)
Tr:実効温度(樹冠上の気温の代表値)(℃)
Vp:蒸気圧(hPa)(気象庁大手町露場の観測値、2014年12月2日以後は北の丸露場)
U:風速(北の丸公園、測風塔高度=35m)(m/s)
H:顕熱フラックス観測値(W/m2)
lE:潜熱フラックス観測値(W/m2)
β:フラックスの計算値が観測値にもっとも適合する蒸発効率(無次元)
個数:上記条件で選んだ、10-15時のHとlEがともに観測された日数
月 Rn R↓ G Q Tr Vp U H lE 個数 β H lE
計算 計算
1 >300 690 152 537 8.8 3.23 3.4 125 53 23 0.08 114 48
2 >300 794 193 602 9.7 3.98 3.2 180 58 29 0.07 166 47
3 >500 979 202 777 18.7 6.99 3.3 246 119 18 0.08 220 107
4 >500 1046 178 869 20.5 7.16 3.9 268 179 33 0.09 253 150
5 >500 1069 87 982 23.1 9.43 3.8 213 332 13 0.19 197 313
6 >600 1130 77 1053 28.2 16.41 3.9 141 444 11 0.25 133 427
7 >600 1167 126 1041 32.3 25.80 4.0 86 460 6 0.27 88 441
8 >800 1148 49 1098 33.0 27.60 4.1 81 519 8 0.30 86 497
9 >300 1038 148 890 29.4 20.34 3.3 85 329 16 0.26 62 340
10 >300 867 133 734 21.0 10.70 3.7 80 229 15 0.23 75 221
11 >300 719 130 589 15.2 6.61 3.4 62 135 21 0.19 58 129
12 >300 668 118 551 9.8 3.95 4.6 110 77 4 0.10 108 64
平均 - 943 133 810 20.8 11.85 3.7 140 245 - 0.18 130 232
付録9 熱収支式を解いて顕熱・潜熱輸送量を計算する方法
熱収支式と顕熱輸送量H・潜熱輸送量lEのバルク式は次のように表される。σ:ステファン-ボルツ
マン定数、Cp:空気の定圧比熱、ρ:空気密度、Te:森林の実効的な温度、qsat(Te):Teに対する
飽和比湿、T:気温、l:水の気化の潜熱とすれば、
R↓=σTe4+H+lE+G ・・・・・・ (a1)
H=Cpρga(Te-T) ・・・・・・・・・・ (a2)
lE=lρβga{qsat(Te)-q)} ・・・・・(a3)
ここに、
入力放射量:R↓=(S↓-S↑)+L↓
交換速度:ga=ChU
これら3式(a1, a2, a3)を逐次近似の方法で解き、Te と H と lE をもとめる。植生密度が比較的高
い森林の場合(自然教育園など)、gaとして式(9)を用いる。蒸発効率として
図123.15(下)の緑曲線を用いる。逐次近似の計算プログラムは「地表面に近い大気の科学」
の付録Fのプログラムを数行変更すればよい。
長時間の降雨日は、β=1とする。遮断蒸発量の評価についての詳細は近藤・中園・渡辺
(1992)、近藤・中園・渡辺・桑形(1992)に示されている。
引用文献
Kondo J. and T. Watanabe, 1992: Studies on the bulk transfer coefficients over a vegetated
surface with a multilayer energy budget model. J. Atmos. Sci., 49, 2183-2199.
近藤純正、1982:大気境界層の科学.東京堂出版、pp.219.
近藤純正(編著)、1994:水環境の気象学―地表面の水収支・熱収支―.朝倉書店、pp.350.
近藤純正、2000:地表面に近い大気の科学-理解と応用.東京大学出版会、pp.324.
近藤純正、2012:日本の都市における熱汚染量の経年変化.気象研究ノート、224号、25-56.
近藤純正・桑形恒男・中園 信、1991:地域代表風速の推定法.自然災害科学、10(3)、
171-185.
近藤純正・渡辺 力・中園 信、1992:日本各地の森林蒸発散量の熱収支評価.天気、39(11)、
685-695.
近藤純正・渡辺 力・中園 信・石井正典、1992:森林における降雨の遮断蒸発のモデル計算.
天気、39(3)、159-167.
近藤純正・石井正典、1992:熱収支法による遮断蒸発量の推定と観測の比較.水文・水資源学会誌、
5(1)、27-34.
近藤純正・中園 信・渡辺 力、1992:日本の水文気象(2)-森林における降雨の遮断蒸発量―.
水文・水資源学会誌、5(2)、29-36.
近藤純正・中園 信・渡辺 力・桑形恒男、1992:日本の水文気象(3)-森林における蒸発散量―.
水文・水資源学会誌、5(4)、8-18.
近藤純正・桑形恒男・中園 信、1992:地域代表風速の推定法.自然災害科学、10、
171-186.
近藤純正・中園 信、1993:日本の水文気象(4)-地域代表風速、熱収支の季節変化、
舗装地と芝生地の蒸発散量.水文・水資源学会誌、6(1)、9-18.
渡辺 力:2001:落葉樹林への適用例、地表面フラックスの測定法.気象研究ノート、第199号、
177-182.


















