Uncletel's パソコン備忘録

　　● 制御点が３点と４点の時の計算式を作ってみる。
　　　曲線（ベジェ曲線）の作り方（図式）では、図を使って曲線(ベジェ曲線)上の点を求めてみました。
　　　しかしコンピュータでは図からではなく計算式から、求めなくてはなりません。
　　　それでは、計算式を、図を基に作って見ます。
　　　その前に、次の事柄を頭に入れておいてください。
　　　　1.　各点は、x、y、z座標からなっています、従って求めた式からx、y、z座標を求めるためには、同じ式を使ってそれ
　　　　　　ぞれの座標を求めます。
　　　　2.　内分比から点を求める方法は次のようになります。
　　　　　　P(u) = Q₀(1.0 - u) + Q₁u
　　　　　　例）始点Q₀が３で、終点Q₁が５で、uが0.4(10等分の4等分目)の値を求める
　　　　　　┣━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━┫
　　　　　Q₀=３←────────→P(u)←──────────────→Q₁=５
　　　　　　┗━━━━━━━━━━━┻━━━━━━━━━━━━━━━━━┛
　　　　　　　　u = 4/10 = 0.4←────────→( 1.0 - u ) = 0.6

　　　　　　P(u) = Q₀(1.0 - u) + Q₁u = 3 X 0.6 + 5 X 0.4 = 3.8となります。
　　　　　　※小学校高学年レベルの算数なので思い出しておいてください。

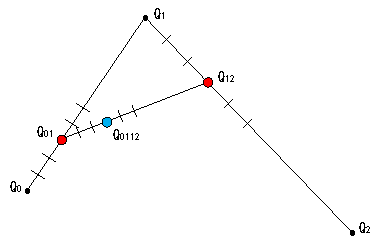
　　　　それでは、制御点が３点の場合の曲線上の点を求める式を求めてみましょう。

図１

　　　　Q₀₁₁₂を求める。
　　　　　内分比を使って求めると、次のようになります。
　　　　　Q₀₁₁₂ = Q₀₁(1.0 - u) + Q₁₂u -----(1)
　　　　　Q₀₁ = Q₀(1.0 - u) + Q₁u -----(2)
　　　　　Q₁₂ = Q₁(1.0 - u) + Q₂u -----(3)
　　　　　(2)と(3)を(1)へ代入すると次のようになります。

　　　　　Q₀₁₁₂ = (Q₀(1.0 - u) + Q₁u)(1.0 - u) + (Q₁(1.0 - u) + Q₂u )u
　　　　　これを展開すると
　　　　　Q₀₁₁₂ =
　　　　　整理すると次のようになります。
　　　　　P(u) = Q₀₁₁₂ =
　　　　　Pは、u が変化する度に求まる点なので、u はPのパラメータと呼ばれます。(※ u は内分比なので、0.0≦ u ≦1.0)

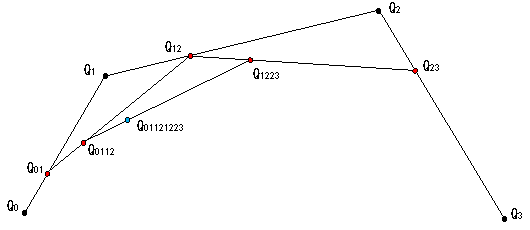
　　　　次に、制御点が４点の場合の曲線上の点を求める式を求めてみましょう。

図２

　　　　Q_01121223を求める。
　　　　　内分比を使って求めると、次のようになります。
　　　　　Q_01121223 = Q₀₁₁₂(1.0 - u) + Q₁₂₂₃u --------------------(1)
　　　　　Q₀₁₁₂ = Q₀₁(1.0 - u) + Q₁₂u --------------------(2)
　　　　　Q₁₂₂₃ = Q₁₂(1.0 - u) + Q₂₃u --------------------(3)
　　　　　Q₀₁ = Q₀(1.0 - u) + Q₁u --------------------(4)
　　　　　Q₁₂ = Q₁(1.0 - u) + Q₂u --------------------(5)
　　　　　Q₂₃ = Q₂(1.0 - u) + Q₃u --------------------(6)
　　　　　(4)と(5)と(6)を(2)と(3)へ代入すると次のようになります。
　　　　　Q₀₁₁₂ = (Q₀(1.0 - u) + Q₁u)(1.0 - u) + (Q₁(1.0 - u) + Q₂u)u
　　　　　　　　　= --------------------(2')
　　　　　Q₁₂₂₃ = (Q₁(1.0 - u) + Q₂u)(1.0 - u) + (Q₂(1.0 - u) + Q₃u)u
　　　　　　　　　= --------------------(3')
　　　　　さらに(2')と(3')を(1)へ代入すると次のようになります。

　　　　　Q_01121223 =
　　　　　これを展開すると
　　　　　Q_01121223 =
　　　　　整理すると次のようになります。
　　　　　P(u) = Q_01121223 =
　　　　　Pは、u が変化する度に求まる点なので、u はPのパラメータと呼ばれます。(※ u は内分比なので、0.0≦ u ≦1.0)

　　　これで、制御点が３点の場合と、制御点が４点の場合の式が出来上がりました。

　　● 曲線(ベジェ曲線)の一般式を作ってみる。
　　　次に、制御点が何点の場合でも対応できる、さらなる一般式を求めてみたいと思います。

　　　　制御点が３点の場合の式：P(u) = --------------------(7)
　　　　制御点が４点の場合の式： P(u) = --------------------(8)
　　　　を次のように書き換えてみます。
　　　　制御点が３点の場合の式：P(u) = --------------------(9)
　　　　制御点が４点の場合の式：P(u) = --------------------(10)
　　　　ここで u の０乗は１です、ちなみにどのような値も０乗すると１になります。
　　　　通常１のかけ算では１は書かないので、(9)と(7)、(10)と(8)は同じ式です。

　　　　ここで(10)式を見てみましょう。
　　　　 P(u) =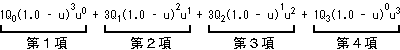

　　　　各項は、内分比に対する制御点の混合割合の値を示しています。
　　　　ここで各項の係数は見てみましょう。

　　　　 (9)と(10)の式の係数を並べて書いてみます、さらに制御点が５点の場合も書いてみると下記のようになります。
　　　　

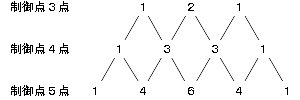
　　　　これは有名なパスカルの三角形と言われる物で、高校１年のときにお目にかかった人も多いのではと思います。
　　　　このパスカルの三角形には多くの数列が含まれています、また最短経路問題とも関連しています。
　　　　パスカルの三角形は、二項展開における係数を三角形状に並べた物です。この係数を二項係数といいます。
　　　　

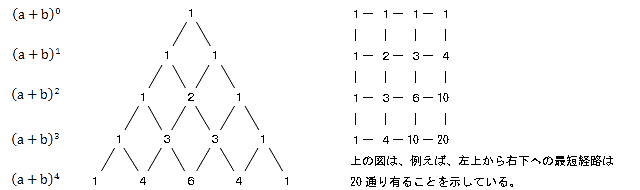
　　　　この二項係数は、次式により求められます。

　　　　c( n, i ) = _nC_i = 　　　　　※ただし、n! = n・(n - 1)・(n - 2)．．．3・２・1 (nの階乗)
　　　　例) 3! = 3・2・1 = 6 で、また 0! = 1であり、1! = 1 です。
　　　　c( n, i ) では、制御点が４点(n = 3)の場合、 i = 0で第1項の係数, i = 1で第2項の係数, i = 2で第3項の係数, i = 3で第4項の係数です。
　　　　したがって、(10)式を一般式で書くと次式になります。

　　　　P(u) = -------------------(11)
　　　　※ただし、0.0 ≦ u ≦ 1.0

　　　● 級数(数列の和)について
　　　　これは数列の和で、この場合には i が変わる度に加算して行く事を意味しています。
　　　　　例）
　　　　　　S =
　　　　　　上記の式は、 S = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 と同じ意味です。

　　　　よって、(11)式では、制御点が４点( n = 3 )の場合、i = 0 のとき第１項、i = 1 のとき第２項、i = 2 のとき第３項、i = 3 のとき第４項、
　　　　が求まり、加算すると 内分比 u に対する曲線(ベジェ曲線)上の点が求まる事になります。

　　　● 計算例
　　　　制御点が、Q₀(x = 10.0, y = 20.0, z = 50.0) Q₁(x = 20.0, y = 50.0, z = 30.0) Q₂(x = 30.0, y = 10.0, z = 10.0) の時の
　　　　ベジェ曲線上の点を求める。( n = 2 )
　　　　u = 0.0、u = 0.2、u = 0.4、u = 0.6、u = 0.8、u = 1.0の時の Px, Py, Pz を求めてみます。
　　　　(※ u = 0.1、u = 0.3、u = 0.5、u = 0.7、u = 0.9 の時の Px, Py, Pz は、計算してみてください。)
　　　　Px_(0.0) = 1・(1.0 - 0.0)^{(2 - 0)}・0.0⁰・10.0 + 2・(1.0 - 0.0)^{(2 - 1)}・0.0¹・20.0 + 1・(1.0 - 0.0)^{(2 - 2)}・0.0²・30.0 = 10.0
　　　　Py_(0.0) = 1・(1.0 - 0.0)^{(2 - 0)}・0.0⁰・20.0 + 2・(1.0 - 0.0)^{(2 - 1)}・0.0¹・50.0 + 1・(1.0 - 0.0)^{(2 - 2)}・0.0²・10.0 = 20.0
　　　　Pz_(0.0) = 1・(1.0 - 0.0)^{(2 - 0)}・0.0⁰・50.0 + 2・(1.0 - 0.0)^{(2 - 1)}・0.0¹・30.0 + 1・(1.0 - 0.0)^{(2 - 2)}・0.0²・10.0 = 50.0

　　　　Px_(0.2) = 1・(1.0 - 0.2)^{(2 - 0)}・0.2⁰・10.0 + 2・(1.0 - 0.2)^{(2 - 1)}・0.2¹・20.0 + 1・(1.0 - 0.2)^{(2 - 2)}・0.2²・30.0 = 14.0
　　　　Py_(0.2) = 1・(1.0 - 0.2)^{(2 - 0)}・0.2⁰・20.0 + 2・(1.0 - 0.2)^{(2 - 1)}・0.2¹・50.0 + 1・(1.0 - 0.2)^{(2 - 2)}・0.2²・10.0 = 28.4
　　　　Pz_(0.2) = 1・(1.0 - 0.2)^{(2 - 0)}・0.2⁰・50.0 + 2・(1.0 - 0.2)^{(2 - 1)}・0.2¹・30.0 + 1・(1.0 - 0.2)^{(2 - 2)}・0.2²・10.0 = 42.0

　　　　Px_(0.4) = 1・(1.0 - 0.4)^{(2 - 0)}・0.4⁰・10.0 + 2・(1.0 - 0.4)^{(2 - 1)}・0.4¹・20.0 + 1・(1.0 - 0.4)^{(2 - 2)}・0.4²・30.0 = 18.0
　　　　Py_(0.4) = 1・(1.0 - 0.4)^{(2 - 0)}・0.4⁰・20.0 + 2・(1.0 - 0.4)^{(2 - 1)}・0.4¹・50.0 + 1・(1.0 - 0.4)^{(2 - 2)}・0.4²・10.0 = 32.8
　　　　Pz_(0.4) = 1・(1.0 - 0.4)^{(2 - 0)}・0.4⁰・50.0 + 2・(1.0 - 0.4)^{(2 - 1)}・0.4¹・30.0 + 1・(1.0 - 0.4)^{(2 - 2)}・0.4²・10.0 = 34.0

　　　　Px_(0.6) = 1・(1.0 - 0.6)^{(2 - 0)}・0.6⁰・10.0 + 2・(1.0 - 0.6)^{(2 - 1)}・0.6¹・20.0 + 1・(1.0 - 0.6)^{(2 - 2)}・0.6²・30.0 = 22.0
　　　　Py_(0.6) = 1・(1.0 - 0.6)^{(2 - 0)}・0.6⁰・20.0 + 2・(1.0 - 0.6)^{(2 - 1)}・0.6¹・50.0 + 1・(1.0 - 0.6)^{(2 - 2)}・0.6²・10.0 = 30.8
　　　　Pz_(0.6) = 1・(1.0 - 0.6)^{(2 - 0)}・0.6⁰・50.0 + 2・(1.0 - 0.6)^{(2 - 1)}・0.6¹・30.0 + 1・(1.0 - 0.6)^{(2 - 2)}・0.6²・10.0 = 26.0

　　　　Px_(0.8) = 1・(1.0 - 0.8)^{(2 - 0)}・0.8⁰・10.0 + 2・(1.0 - 0.8)^{(2 - 1)}・0.8¹・20.0 + 1・(1.0 - 0.8)^{(2 - 2)}・0.8²・30.0 = 26.0
　　　　Py_(0.8) = 1・(1.0 - 0.8)^{(2 - 0)}・0.8⁰・20.0 + 2・(1.0 - 0.8)^{(2 - 1)}・0.8¹・50.0 + 1・(1.0 - 0.8)^{(2 - 2)}・0.8²・10.0 = 23.2
　　　　Pz_(0.8) = 1・(1.0 - 0.8)^{(2 - 0)}・0.8⁰・50.0 + 2・(1.0 - 0.8)^{(2 - 1)}・0.8¹・30.0 + 1・(1.0 - 0.8)^{(2 - 2)}・0.8²・10.0 = 18.0

　　　　Px_(1.0) = 1・(1.0 - 1.0)^{(2 - 0)}・1.0⁰・10.0 + 2・(1.0 - 1.0)^{(2 - 1)}・1.0¹・20.0 + 1・(1.0 - 1.0)^{(2 - 2)}・1.0²・30.0 = 30.0
　　　　Py_(1.0) = 1・(1.0 - 1.0)^{(2 - 0)}・1.0⁰・20.0 + 2・(1.0 - 1.0)^{(2 - 1)}・1.0¹・50.0 + 1・(1.0 - 1.0)^{(2 - 2)}・1.0²・10.0 = 10.0
　　　　Pz_(1.0) = 1・(1.0 - 1.0)^{(2 - 0)}・1.0⁰・50.0 + 2・(1.0 - 1.0)^{(2 - 1)}・1.0¹・30.0 + 1・(1.0 - 1.0)^{(2 - 2)}・1.0²・10.0 = 10.0

　　　● そして、曲面へ
　　　　これを平面に拡張すると、ベジェ曲面になり、次式で表します。
　　　　

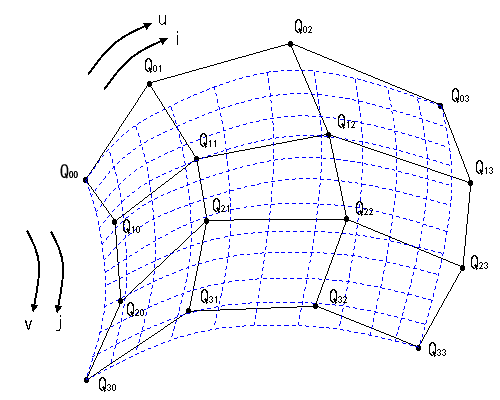
　　　　S(u, v) = --------------------(12)
　　　　※ただし、0.0 ≦ u, v ≦ 1.0
　　　　(12)式は、一般に次のように表現されています。
　　　　S(u, v) =
　　　　B_jm(v) = C( j, m )・( 1.0 - v )^m-j・v^j
　　　　B_in(u) = C( i, n )・( 1.0 - u )^n-i・uⁱ
　　　　これは、バーンスタインの基底関数と呼ばれるもので、B はその頭文字です。またS(u, v)の S は Surface(表面)の
　　　　頭文字です。