図形処理
曲線(ベジェ曲線)の作り方を図を使って理解します。
ベジェ曲線は、いくつかの制御点を与えることによって描かれる曲線です。
下の図は、制御点を3点(Q0〜Q2)与えていますが、4点、5点・・・と何点与えても構いません。
3点の場合は2次曲線になり、4点 では3次曲線、5点では4次曲線になります。
すなわち、制御点の数から１引いたものが、曲線の次数になります。次数が増えると複雑な曲線を描くことができますが、
その分 計算量も増えます。
また、線分を何等分するかによって曲線の滑らかさが変わります。経験から10等分もしくは20等分が良いと 思われます。
※下図では、10等分で説明しています。
● 曲線(ベジェ曲線：３点の場合)を作図により求めてみる。
|
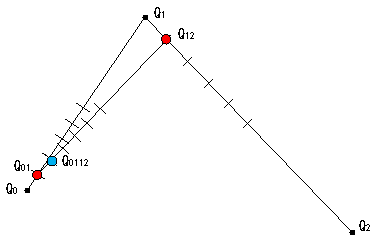
図１ |
１等分目 次に、線分Q1Q2のQ1から1等分目の点Q12を描きます。 さらに線分Q01Q12のQ01から1等分目の点Q0112を描きます。 これが、曲線上の1等分目の点になります。 |
|
|
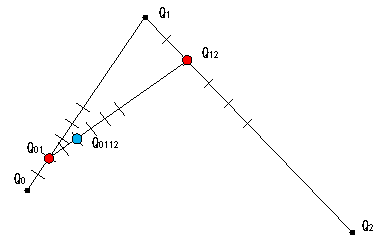
図２ |
２等分目 次に、線分Q1Q2のQ1から2等分目の点Q12を描きます。 さらに線分Q01Q12のQ01から2等分目の点Q0112を描きます。 これが、曲線上の2等分目の点になります。 |
|
|
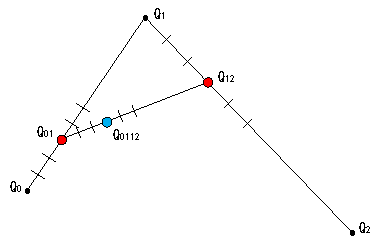
図３ |
３等分目 次に、線分Q1Q2のQ1から3等分目の点Q12を描きます。 さらに線分Q01Q12のQ01から3等分目の点Q0112を描きます。 これが、曲線上の3等分目の点になります。 |
|
|
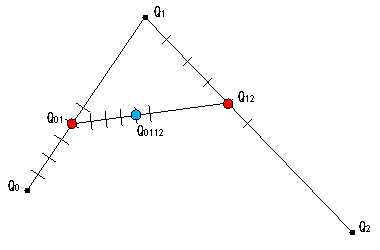
図４ |
４等分目 次に、線分Q1Q2のQ1から4等分目の点Q12を描きます。 さらに線分Q01Q12のQ01から4等分目の点Q0112を描きます。 これが、曲線上の4等分目の点になります。 |
|
同様に5等分目から9等分目までを繰り返して
を求めていきます。出来上がった点をQ0から順番にQ2までつないでいくと曲線が
出来上がります。
これが、ベジェ曲線の図形的な作り方です。
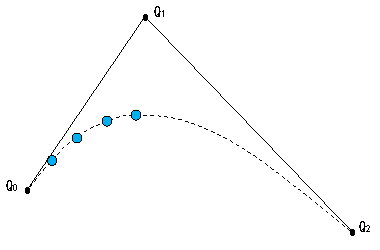
図５
● 曲線(ベジェ曲線：４点の場合)を作図により求めてみてください。
制御点を４点(Q0〜Q3)与えて、制御点の位置をいろいろ変えて曲線を描いてみてください。作り方は図１から図４の方法とまったく
同じです。
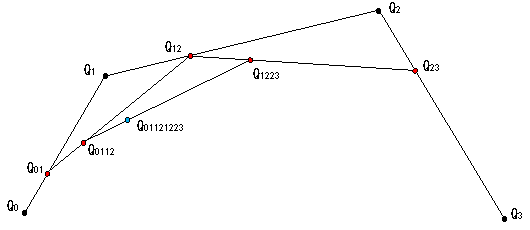
参考図
