2011.02.09-16
再生産数のガンマ分布
パラメータ k=0.1 だと、感染者が 100人以下位になった時(新規感染者数でいうと10数人以下)、感染プロファイルからの感染者数予測に誤差が大きくなる。こういうときでも実効再生産数 Rt はちゃんと計算しているので、どうなっているのだろう、と思って、調べてみた。下記の方法がよく使われているようである。
A.Cori et al. "A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics", American Journal of Epidemiology, Vol. 178, No. 9, DOI: 10.1093/aje/kwt133, Advance Access publication:September 15, 2013.
● 予備知識
Rt はその時点での再生産数である。発症観測終了時点から潜伏期間だけ前の時点 t で確定するが、それより新しい時点では暫定的となる。発症者の検査が遅れれば、更に暫定期間が長くなる。
新規感染者数=It として、感染から s 日後の infection probability を ws とすると、
Rt= It/{Σs I(t-s)ws} :
< BR> ここでは、区別するために、下付きを( ) に入れた。ws は規格化されている(和が 1)。
と定義される。簡単に説明すると、一人の感染者が生み出す二次感染者数そのものの時間変化を Ws とすれば、その総和が Rt であるから、
It=Σs I(t-s)Ws=Σs I(t-s)ws・Rt; Rt=ΣsWs
(この考え方の背後にあるのは、ws は変化せず、つまり感染力 Ws の時間依存性は変化せず、単にその大きさだけが変化する、ということである。これは感染対策が行動自粛や自衛の場合には正しいが、隔離政策による場合は感染力の期間が短くなるので、必ずしも成り立たない。しかし、観測の精度を考えるとその違いの影響は非常に少ないと思われる。)
感染対策をすればその日の新規感染者数が変化するから、これは瞬時に効果が反映される筈のものである。しかし、実際にはその時点での新規感染者数というのは後にならないと判らない。そこから発症までには潜伏期間(incubation time)があり、発症から検査までも検査遅れ時間がかかり、更に検査結果から公表までの時間もある。通常は発症日が記録されるから、発症日ベースでの新規感染者数プロファイルを得て、そこから潜伏期間だけ遡って新規感染時ベースでの感染者数プロファイルを得る。潜伏期間には広い分布があるので、これは結構面倒な逆算 になる。(簡便には平均の潜伏期間だけ一様に遡るという手もあるが、時間分解能が下がる。)いずれにしても、こうして、It が得られる。この論文で扱うのは、その後の計算である。
次は ws である。これは感染してから二次感染させるまでの時間 s についての分布である。規格化してある。通常 generation time distribution と呼ばれるが、感染という事象は、実験でもしないと直接観測することができないので、serial time distribution で代用されることが多い。これは 発症から二次感染者の発症までの時間間隔分布である。発症から二次感染までの時間が潜伏期間と相関していない場合は同じと見做してよい。(新型コロナでは相関がある(Ferretti et al.)のであるが、まあそれほどの違いは生じないと思われる。二次感染は一次感染からの経過時間よりも、発症日からの経過時間の方に強く関係していることが知られている(Ferretti et al.)から、発症時点を基準とした感染力分布 TOST を使う方が良いかもしれない。その時は分母の I(t-s) が発症日基準の感染者数になるだけである。)
もう一つ重要なパラメータは平均区間 τ である。毎日のベースで Rt を計算すると変動が大きくて、計算できない場合すら生じるので、τ 日の間は Rt が一定であるとしてデータ数を増やして計算する。これによって、信頼性区間が狭まる。 ws についても推定誤差があるので、それも Rt の推定誤差に取り込むことができるということである。
Rtc という再生産数もよく使われる。これは cohort reproduction number と呼ばれる。過去の完結したデータから推定された再生産数であるので、性格上その時点での評価ではなく、将来予測に使われる。感染モデルから直接得られる再生産数もその中に入る。
● Baysian Method による Rt の計算
It と ws から Rt を計算する方法については、Baysian Method を使う。原論文としては、Fraser C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS One. 2007;2(1):e758 であるが、Appendix で説明してあるのでそれを読んだ。
以下数式がややこしいので、まずは τ=1 の場合を説明する。観測された日々の新規感染者数 It は 推定される 再生産数×関与する感染者数 からたまたまランダムに実現した変数であると考える。つまり、n=Rt{Σs I(t-s)ws} をパラメータとする ポワッソン分布である。
It=z ~ n^z・exp(-n)/z! : n=Rt{Σs I(t-s)ws}
となる。ここで、Rt の「事前分布」をパラメータ (a,b) のガンマ分布と仮定する。すなわち
Rt=x ~ x^(a-1)・exp(-x/b)/Γ(a)b^a
である。平均値<Rt>=ab、分散=ab^2
となる。(このスキームは It の分布として負の二項分布を与える筈である。Superspreader の時との対応で言えば、k=a である。)
以下ΣsI(t-s)ws=Λと略記する。紛らわしいが Λ は^べき乗ではなく、ラムダ。
「Rtが与えられた条件下でItが実現する」確率P(It|Rt)は期待値RtΛのポワッソン分布である。これに「Rtとなる」事前確率(上記ガンマ分布)を掛ければ、「Rtであって、且つItである」確率が得られるが、これは「Itであって、且つRtである」確率と同じである(a,bの分布と見れば尤度分布)。今、観測値としてItが得られているのであるから、Itとなる確率が1となっており、この情報を得た時点で、これはそのまま「Rtとなる」事後確率に比例する。これがベイズ流のパラメータ推定である。実際にその確率を計算してみると、(x=Rt、z= It とおく)、
(z,x) ~ (xΛ)^z・exp(-(xΛ))/z!・x^(a-1)・exp(-x/b)/Γ(a)b^a
=x^(a+z-1)・exp(-x(Λ+1/b))・Λ^z/(z!Γ(a)b^a)
となって、これは x についていえば、パラメータ (a+z,1/(Λ+1/b)) のガンマ分布になっている。
つまり、事前分布と事後分布はいずれもガンマ分布であって、z と Λ という情報を得て、パラメータが事前 (a,b) から事後 (a+It、1/(Λ+1/b)) へと変更される。
τ が 2以上の時には、新規感染者数が t、t-1、、、t-τ+1 での値となるから、再生産数が Rtτ となる条件下での、その確率は、個別の新規感染者数を与える確率の積になる。事後確率分布のパラメータは (a+ΣIs、1/(ΣΛ+1/b)) となる。ここで、Σ は過去の値を t~t-τ+1 まで加えるという意味である。
(なお、ws に TOST を使う時は、当然ながら、Λ の定義は新規発症者数から計算することになる。)
再生産数の期待値<Rt>=(a+ΣIs)/(ΣΛ+1/b)、
分散=(a+ΣIs)/(ΣΛ+1/b)^2、
となる。
エクセルマクロが公開されている。wsについては直接与えることもできるし、潜伏期間データを入れて計算させることも出来るし、パラメータ(歪ガンマ分布)を与えることもできる。事前分布パラメータ(a,b)も選べる。著者は(1,5)を使っている。これはR0=5、k=1 に相当する。この事前分布の設定が事後分布に与える影響がどれ位なのかも Appendix で計算していて、大した違いは生じない。それと、このやり方だと、Rt の期待値 ab と k=a
が得られることになる。kの方はあまり注目されていないようで、よく見かけるのは95%信頼区間である。
● Baysian というほどの意味はあるのか?
さて、再生産数の期待値と分散の式の中の (a+ΣIs) は a という定数+τ回に亘る新規感染者数の和であるから、a は相対的に小さくなって、あまり関係ない。(ΣΛ+1/b) は 1/b という定数+過去の(大まかには generation time だけ過去の)新規感染者数の和であるから、1/b もあまり関係ない。要するに、期待値としては、現在の新規感染者数÷generation time だけ過去の新規感染者数 である。標準偏差÷期待値としては、現在の新規感染者数の平方根の逆数、となる。これはまた随分小さい。少なくとも分散については計算する意味が無いのではないか?
事前分布として (a,b)=(1,∞) とすれば、均一分布である。ポワッソン分布 (xΛ)^z・exp(-(xΛ))/z! を逆に x についての分布と見れば良い。この場合分布の最大での x=z/Λ となる。パラメータは (1+z、1/Λ)だから、期待値 <x>=(1+z)/Λ。
結局の処、この Cori の方法は実質的には、ポワッソン分布を与えるパラメータとしての RtΛ の推定 であって、信頼区間というのはその推定の信頼区間である。Rt の分布パラメータ (a,b) の推定を行っているわけではない。だとすれば、こんな事をやらなくても、単に x=z/Λ として、Rt を推定し、その推定誤差として標準偏差=√z/Λ とすれば良い。信頼区間としては xΛ に対する信頼区間をポワッソン検定から求めればよい。R では poisson.test(z)として、頻度パラメータ λ の95%信頼区間を得て、これを Λ で割る。λ の期待値は z に決まっているので、想定される dpois(z,λ) 分布の95%範囲に z は入るような λ の範囲を λ の信頼区間とすればよい。(https://oku.edu.mie-u.ac.jp/~okumura/stat/CI/)実際に、公開されている計算例(https://www.mhlw.go.jp/content/10900000/000654495.pdf)で確かめてみた。1週間平均とあるから、7日分の新規感染者数が z であり、Rt の平均値から、7日分の Λ和を逆算しておく。z から poisson.test(z) で、95%信頼区間が得られるので、それに Λ和で割れば、公開されている 95%信頼区間が得られる。
なお、ポワッソン分布母平均の 1-α 両側信頼区間は、χ2 分布からも計算できる。
下限値の2倍が、自由度 2z の χ2分布積算の α/2 点、エクセルでは、CHIINV(1-α/2,2z)、R では、qchisq(α/2,2z)。
上限値の2倍が、自由度 2z+2 の χ2分布積算の 1-α/2 点、エクセルでは、CHIINV(α/2,2z+2)、R では、qchisq(1-α/2,2z+2)。
● 実例
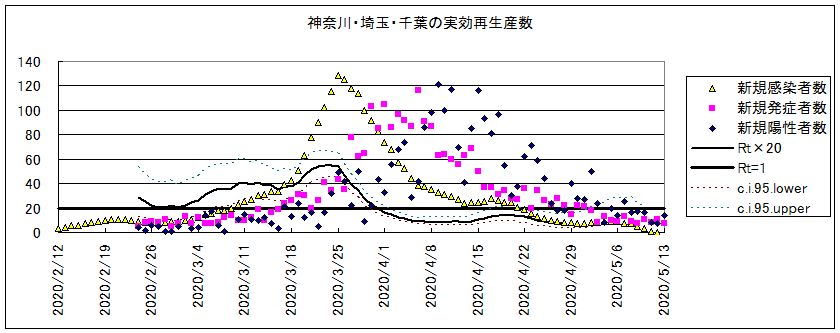
(この段落は追加)試みに、後で使う神奈川・埼玉・千葉の発症数データから感染者数データを逆算して、Ferretti et al. の感染力分布 TOSTを使い、実効再生産数を計算してみた。TOST はほぼ発症日に中心を持つ比較的狭い分布なので、Λの分布は発症者数の分布を平滑化したようなものになっているが、図が混んでくるので省略してある。3月25日から Rt が下がり始めて、31日に 1 を切っている。この頃新規陽性者数は上がり始めた処であるが、志村けんの死亡や小池都知事の発言等による市民の警戒感によって自粛が進んだことを示している。緊急事態宣言が出たのは4月7日であるから、それが果たして必要だったのか、あるいは5月25日まで続ける必要があったのか、という議論が起こるのも無理はないが、この警戒感を継続させた、という意味はあったのだろう。継続していなければ再び感染者が増加したであろう。なお、4月6日までの新規陽性者と発症日のデータだけから計算してみると、3月25日の新規感染者と Rt の減少傾向は判断できないので、宣言自体には合理性があったと思われる。こういう評価には、確かに感染日の逆算の意義がある。
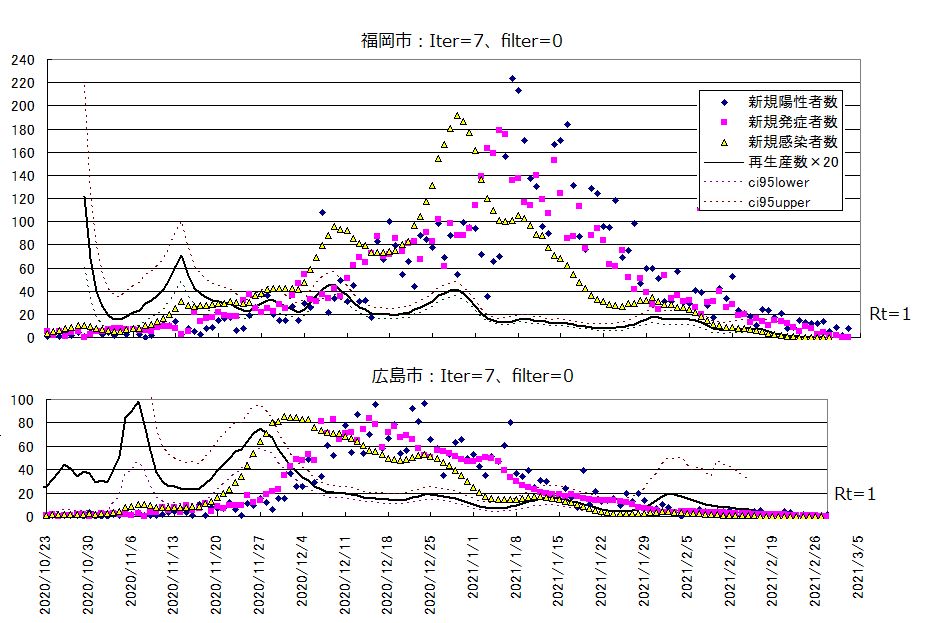
最近の福岡市と広島市についても計算してみた。広島市では12月28日以降は発症日が公表されなくなった。またそれまでも発症日不明の場合がある。これらは発症日から陽性確定日までの時間分布(検査遅延分布)を使って逆算して発症日を与えている。発症日というのは感染力分布の基準となる日という意味で、無症状感染者についても同じような感染力分布をしていると仮定していることになる。逆算に BackProjection を使うと、却って実測の発症日と合わなくなる。これは検査遅延分布が検査日に依存しているからである。感染力分布や潜伏期間分布とは異なり、検査遅延は人間社会の都合で決まるので、どこでも同じとは言えない。そこで、単純に逆算したものを用いた。この方が実測に合う。12月前半までは広島市の方がやや感染拡大が早かったが、広島市は感染対策をかなり積極的に行った為に、収めることができた。もしも放置していたら福岡市のように1月2月まで長引いたであろう。
● Rt の分布を決めることができるだろうか?
本当に Rt の分布の推定をするのであれば、その分布パラメータ (a,b) を決めるために、 x についての畳み込み積分をして、
∫P(z,x)dx =∫x^(a+z-1)・exp(-x(Λ+1/b))・Λ^z/(z!Γ(a)b^a) dx
を考えるべきであろう。そうすれば、これが z を与えるような (a,b) が取り得る尤度分布である。
この中のラプラス積分は、t=x(Λ+1/b) と置きなおして、
∫x^(a+z-1)exp(-x(Λ+1/b))dx=(1/(Λ+1/b)^(a+z))∫t^(a+z-1)exp(-t)dt=Γ(a+z)/(Λ+1/b)^(a+z)
となるので、尤度関数は
∫P(z,x)dx=(Λ^z/z!)/((Λ+1/b)^(a+z))・(Γ(a+z)/Γ(a)b^a)=nbinom(z,a,1/(1+bΛ))
ということになる。対数尤度関数は、
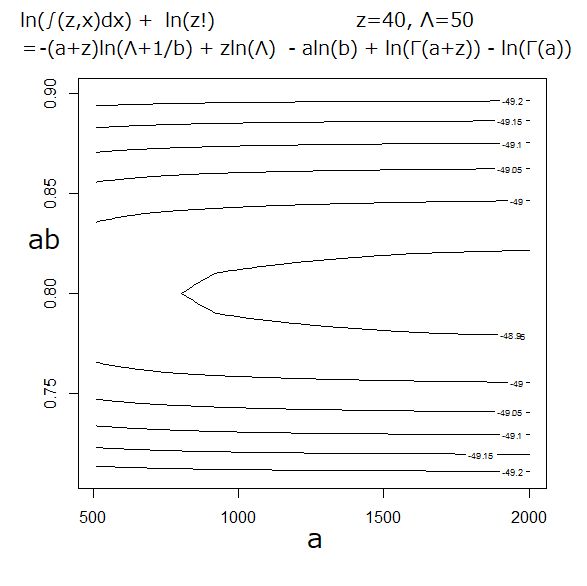
ln(∫(z,x)dx)=-(a+z)ln(Λ+1/b) + zln(Λ) - ln(z!) - aln(b) + ln(Γ(a+z)) - ln(Γ(a))
これを最大化するような (a,b) を求めれば良い。
ln(Γ(x))の微分はポリガンマ関数 ψ(x) というらしい。R では digamma(x) で計算できる。x 正→0 では負方向に発散し、xに対して単調増加関数である。従って、この尤度を a と b に対して最大化するような (a,b) は、対数尤度を微分して計算できる筈である。a で微分して 0 とすると、
-ln(Λ+1/b) - ln(b) + ψ(a+z) - ψ(a) =0
b で微分して 0 とすると、
(a+z) - a(bΛ+1) =0 → abΛ=z
つまり、尤度最大として <Rt>を推定すると、It/Λ となるので予想通りである。
次に、b を消去すると、
- ln((a+z)/a) + ψ(a+z) - ψ(a)=0
これは解析的に解けないだろう。数値的に解いてみると、尤度最大点は a=∞ (x の分散無し)となってしまう。下図は対数尤度の等高線である。
● Rt の分布を求める為に
Cori の方法を整理してみる。まず x=Rt がガンマ分布 Gamma(x,a,b) に従うというのが事前の予測である。x が決まれば、Λはその時点での一次感染者数として、xΛ をパラメータとするポワッソン分布に従って z=It が実現する。つまり、z は Poiss(z,xΛ) に従う。これは x を前提とした上での z が実現する確率である。従って、Poiss(z,xΛ)・Gamma(x,a,b) は (a,b) というパラメータを前提とした上での、(z,x) が実現する確率である。これを逆に読み解くのがベイズの定理で、(a,b,z) を前提とした上での x が実現する確率でもある。しかし、どう読み取っても構わない。ここでは z を前提とした上での、(x,a,b)が実現する確率と読み取る。
Poiss(z,xΛ)・Gamma(x,a,b)
=Gamma(x,a+z,b/(1+bΛ))・{Γ(a+z)(b/(1+bΛ))^(a+z)}/Λ^z/(z!Γ(a)b^a){Γ(a+z)(b/(1+bΛ))^(a+z)}
と変形できるから、更に解釈して、(z,a,b) を固定した上での x が実現する確率と読めば、それはガンマ分布のパラメータが (a+z, b/(1+bΛ)) に変更されただけになる。x の期待値は (a+z)(b/(1+bΛ))、分散は (a+z)(b/(1+bΛ))^2 となる。これが Cori の方法である。この解釈が成り立つには (a,b) の固定が必要である。しかし、そんな仕掛けをしなくても、Poiss(z,xΛ) は x を前提とした z が実現する確率なのだから、これを逆に読んで、z を前提として x が実現する確率(尤度)と解釈するだけで充分である。そうすると、x の期待値は z/Λ、分散は z/Λ^2 である。これは「事前」確率分布として、(0,∞) 、のガンマ分布を想定したのと同じ事である。
次に、∫Poiss(z,xΛ)・Gamma(x,a,b)dx
にはどんな意味があるのだろうか?
∫Poiss(z,x)・Gamma(x,a,b)dx
は負の二項分布 Nbinom(z,a,1/(b+1)) である。本来であれば、個々の感染毎に Rt=x が異なっており、その分布がガンマ分布なのだから、それを独立に Λ回繰り返せば、負の二項分布のパラメータは、再生性の関係から (aΛ,1/(b+1)) になるが、Cori の想定では、Λ回の試行に当たって、同一の x を使う処が違う。その場合は負の二項分布の異方性パラメータ a は変わらず、期待値 ab だけが変わって、(a,1/(bΛ+1)) になる。つまり、そもそも z を RtΛ=xΛ を期待値とするようなポワッソン分布と考えた時点で、Rt には分布が無いことがモデル化されてしまっているのである。だから、Rt の分布をガンマ分布と想定しても、最尤化すれば、(a,b)=(∞,0) ;ab=z/xΛ (x の分散無し)に落ち着いてしまう。
それでは、試行の度に新たに x=Rt を選ぶようにすると、どうなるか? x としてはあらゆる可能性について積分することになり、
∫Poiss(z,x)・Gamma(x,a,b)dx =nbinom(z,a,1/(b+1))、すなわち、一人の感染者が何人に感染させるかの分布は負の二項分布となり、これを Λ回繰り返すから、nbinom(z,aΛ,1/(b+1)) である。対数尤度は、
-(aΛ+z)ln(1+b) - ln(z!) + zln(b) + ln(Γ(aΛ+z)) - ln(Γ(aΛ))
これも最大尤度点は同じく、(a,b)=(∞,0) ;ab=z/xΛ となった。いずれの解釈で推定するにしても、一組のデータ、(z,Λ) では分布パラメータは一つしか決まらない。別の日のデータにおいても、同じ分布パラメータであるとすれば、当然、パラメータが二つ決まるだろう。Cori はそれだけでなく Rt=x までも同じであると仮定したために、結局 Rt の分布が無くなってしまったのである。
● Rt の分布を求めることは出来る!
数日の間分布パラメータ (a,b) が同じであると仮定すれば、その数日分の独立したデータを使って、両方のパラメータを決めることができる。対数尤度は、
∑t {-(aΛ(t)+z(t))ln(1+b) - ln(z(t)!) + z(t)ln(b) + ln(Γ(aΛ(t)+z(t))) - ln(Γ(aΛ(t)))}
となる。b で微分して 0 とすれば、予想通り、
ab=∑t z(t)/∑t Λ(t)
が得られる。また a で微分して 0 とすれば、
∑t Λ(t) ln(1+b) + ∑t {ψ(aΛ(t)+z(t))- ψ(aΛ(t))}=0
となる。
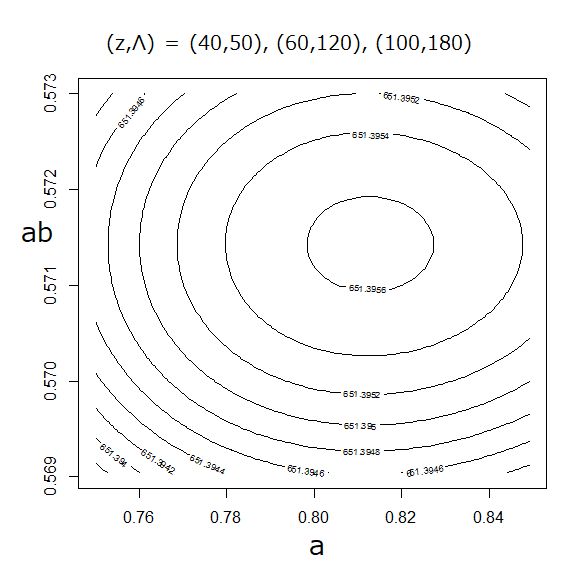
(z,Λ) = (40,50), (60,120), (100,180) という3日分のデータを例として対数尤度を計算してみた。
最大尤度は (ab,a)=(0.5714,0.815) 位となった。原理的にはこれで良いのだろうが、分布が緩やかなので、信頼区間から見て、あまり実際上の意味は無い。