●非線形最小自乗法
負の感染者数を出さないためには、未知数を変えて、感染者数を直接扱うのではなく、その対数を未知数とすればよい。つまり、λt=exp(Xt) として、Xt を未知数とする。こうすると、非線形方程式になってしまうので、反復計算をする必要がある。予測発症者数 Yt の式は同じで、
2021.02.21
発症日ベースの新規感染者数推移から感染日ベースの推移へと変換する方法であるが、なかなか EMS法の良い解説が見つからないので、解説のブログ での結果の式から考察、計算してみた。
感染日 i から発症日 t までの期間(潜伏期間)の分布は f(t-i) で与えられているとする。f が正となる最大の t-i は L であるとする。
発症日での発症者数を Yt、感染日での感染者数の推定値(未知数)を λi として、実測の Yt は パラメータ ∑i f(t-i)λi 、つまり時刻 t で予測される発症者数の期待値をパラメータとするポワッソン分布に従う確率変数であると考える。
Yt ~ (∑i f(t-i)λi)^Yt exp(-∑i f(t-i)λi) /Yt!
である。Yt が継続的に観測されている日数を T とすると、この分布関数の t についての積が、(Y1,Y2,Y3,,,,YT) の実現する確率であり、逆に、その一連の Yt が観測された時には、これが パラメータ ∑i f(t-i)λi の尤度分布である。対数を取って尤度を最大にすることを考えると、
log尤度(λi)=∑t Yt ln{∑i f(t-i)λi} - ∑i f(t-i)λi
である。(定数項は省略)尤度を最大にする条件を導くと、線形方程式となり、特異値分解を使って解いたのが前回の結果
である。
● EMアルゴリズム
EMアルゴリズムは、試行された λ(old) から、より大きな尤度を与えるような λ(new) を下記の式で決める。
λt(new)=λt(old)・F*(T-t)/F(T-t)
ここで、
F(T-t)=∑(d=0~T-t)f(d)
は、t日に感染した発症者の内で、T までに発症すると期待される感染者の比率である。t が小さくなれば(≦T-Lで)、1 になる。
ということは、F* の意味としては、同じ比率のあるべき値であると推定される。
その式は
F*(T-t)=∑(d=0~T-t) f(d) Y(t+d)/Y*(t+d)
となっている。ここで Y(t+d) が実測の発症者数であり、
Y*(t+d)=∑(i=1~t+d) λi(old) f(t+d-i)
から判るように、Y*(t+d) は、設定された解 λ(old) から計算される、t+d 日における期待発症者数である。つまり、Y/Y* は旧推定の λ(old) から予測される t+d 日での発症者数を何倍にすれは良いか、という指標である。その補正比率を f(d) の重み付けで平均したものが、F*/F である。λt の影響は t+d に現れて、その大きさは f(d) に比例しているのだから、これは尤もらしい考え方ではある。
なお、ブログでは、∑が i についての和 ではなく、t についての和 になっている。ミスプリである。また、ここで i の和が i=1 からになっている点が気になる。Y*(t+d) が t+d での期待発症者数であるためには、i の和は t+d-L からでなくてはならない。i の和が 1 からであるということは、t+d < L においては、計算された Y*(t+d) は発症者数の一部にしかならないことを意味する。ただ、対応する初期の Y(t+d)=0 としておけば、その寄与そのものが無くなる。
尤度の式の中の i も 1 から始まっているが、やはり発症を観測された最初の日から始めるべきではないかと思われる。しかし、この式の導出方法がまだ不明なので、これ以上議論は出来ない。
●EMアルゴリズムによる計算
計算は簡単そうなので、FORTRANでプログラムを書いてみた。但し、よく考えないと間違える。。。上記の不明点を考慮して、実測の発症者数推移期間の前に助走期間として、発症者数= 0 の日数を L 日追加した。感染者数 λ を決めなくてはならないからである。ただし、その部分は、一応期待値としての 発症者数が計算されるが、λt からの寄与の一部しか表現していないので、尤度評価の計算からは除外する。使ったデータは前回と同じである。潜伏期間分布 f は 1 ~20日まで、発症数観測データは M=80 日である。反復するにあたっての初期データは逆解、つまり潜伏期間を逆に読んで、観測された発症者数を遡って分布に従って足し合わせたものである。これは分解能は低いが安全サイドの解となっている。
λt(初回)=∑i f(i-j) Yi
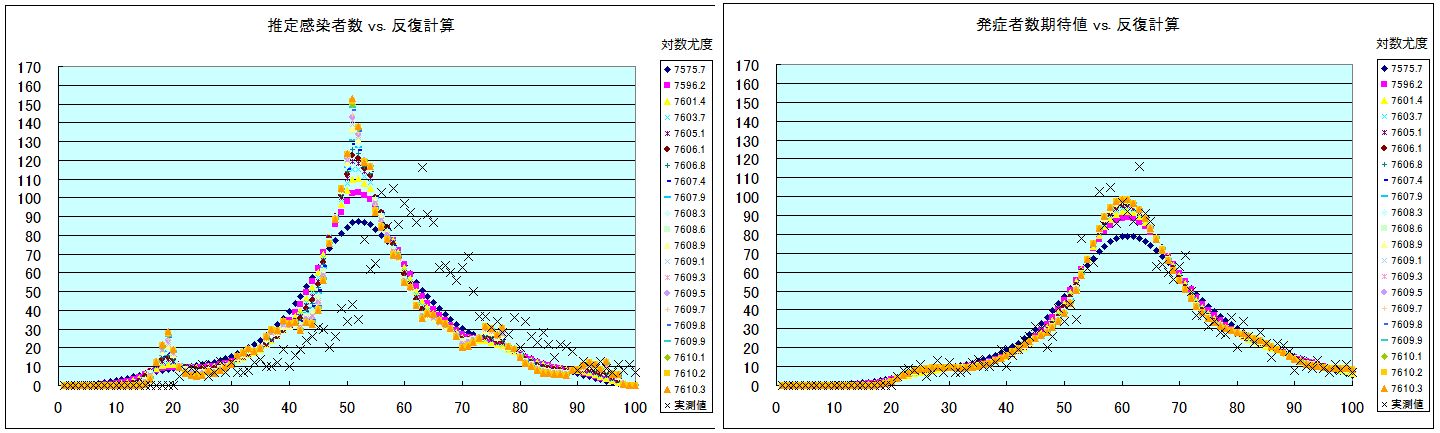
結果は下記グラフである。最初の計算で結構良さそうな解になって、後はゆっくりと感染者数推移のグラフが複雑化していく。20回の反復で計算された対数尤度を右側に表記してある。反復するとピークが尖ってくる。また観測期間の直前のピークが大きくなるのが、不自然である。念の為に、助走期間を無くして計算して見た(この時は f(0)>0 が必要なので、少し変えた。)が、ピークはもっと激しく立ち上がる。実際に10日分のなだらかに発症者数が立ち上がるデータをその前に追加して計算してみたが、やはりピークが出現する。どうやらこれは疑似ピークではなくて、21日から23日にかけての発症者数の増加を反映しているようである。メインのピークも反復を繰り返すと急峻になる。確かに尤度が上がっているので、これはこれで意味があるのかもしれないが、不自然ではある。なお、ピークは反復途中でフィルターを入れる(例えば、{λ(t-1)+2λ(t)+λ(t+1)}/4 で新たに λ(t) に置き換える)と多少丸くなる。これを EMS法といって、実際にはそれが使われるらしい。いずれにしても、どこで反復を止めてよいのか?明確な基準は無いという点では僕の計算 と変わりがないように思われる。。。ただし、解の精度を上げても絶対に負の感染者数が出てこないという処は僕の線形計算よりも優れている。

●非線形最小自乗法
負の感染者数を出さないためには、未知数を変えて、感染者数を直接扱うのではなく、その対数を未知数とすればよい。つまり、λt=exp(Xt) として、Xt を未知数とする。こうすると、非線形方程式になってしまうので、反復計算をする必要がある。予測発症者数 Yt の式は同じで、
Yt=∑j f(t-j)λj=∑j f(t-j)exp(Xj)
である。これから、感度行列 Atj を定義する。
Atj=∂Yt/∂Xt=f(t-j)λj
となる。従って、観測値 Yt(obs) と 予測値 Yt との差異を埋める為の、Xt の補正値 ΔXt は
Yt(obs) - Yt=∑j Atj ΔXj
となる。ΔXj を、パラメータ βで固有ベクトル空間を制限して、特異値分解の手法で解いて、次のステップとして
Xj(new)=Xj(old)+ΔXj
とすればよい。λj で表せば、
λj(new)=exp(ΔXj) λj(old)
ということであるから、exp(ΔXt) がEM法の F*(T-t)/F(T-t) に相当する。(勿論同じではない。)
これは、∑t (Yt(obs) - ∑j f(t-j)λj )^2 を最小化するのと同じ事である。
その時は、正規化方程式、
(∑t Ati Atj) ΔXj=∑t (Yt(obs) - Yt)Atj
を、左辺の行列の対角成分に β×最大固有値 を加えて解く(マルカート法)のと同じ事である。
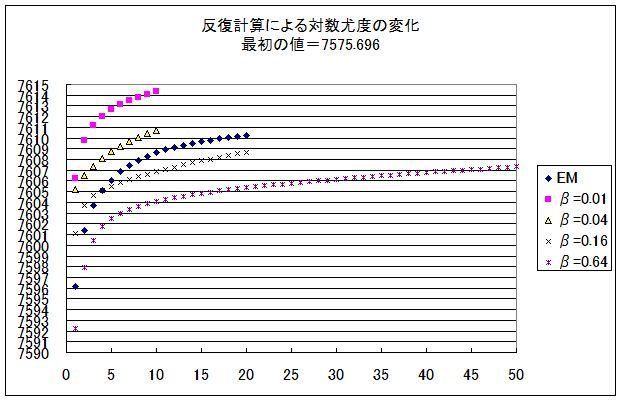
従って、前回の計算と違うのは、感度行列に λj というベクトルが掛かっている処と、反復計算になる処だけである。結果は似たようなものであったが、比較の為に、まず対数尤度が反復回数でどう変化するかを示す。対数尤度を上げるだけなら、非線形最小自乗法の方が手っ取り早いが、推定感染者数推移が「尤もらしい」かどうかが問題である。(対数尤度最大値は、線形計算で負の解を許すと、 β=0 で 7650.593 である。)
そこで、同じ程度の対数尤度での推定感染者数プロファイルの比較をする。7606.4 の近傍を狙って、EM法では5回目と6回目、非線形最小自乗法では、β=0.01の時は1回目、β=0.04の時は2回目、β=0.16の時は8回目、β=0.64の時は35回目である。+印は実測の発症者数である。
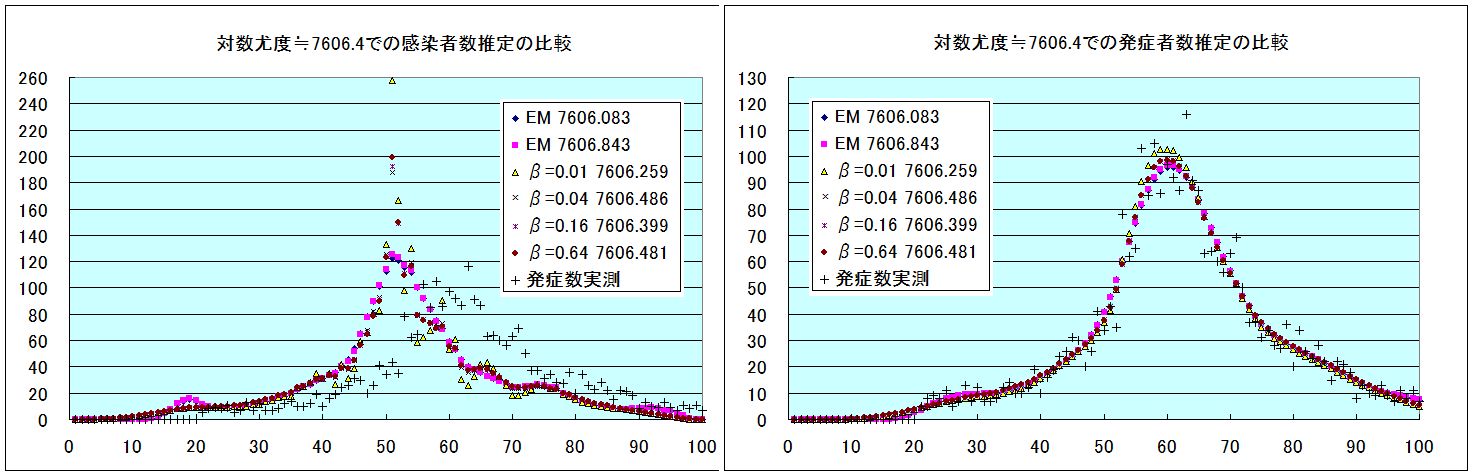
対数尤度を揃えると、βによる差異は小さいが、β=0.01になると、かなり暴れている。EM法と非線形最小自乗法との違いはどのあたりのデータを再現しようとしているかの違いである。非線形最小自乗法では、主ピークが強調されすぎていて、EM法では両端の小さなピークが強調されすぎているように思われる。60日目辺りのプロファイルは非線形最小自乗法の方がよいのではないか、と思われる。
前回のような線形最小自乗法ではメインピークが極端に発達してしまうことはなかったことから、これは変数の対数変換のせいだろうと思われる。
そこで、λj>1 に対しては対数変換をしないことにしてみた。つまり、
λj=exp(xj) and Atj=f(t-j)λj, if λj<1 or xj<0
λj=xj - 1 and Atj=f(t-j), if λj>1 or xj>0
これはうまく行った。しかも、対数尤度が EM 法よりも大きくなる。下図に反復計算の結果を示した。この中の EM2 については後で述べる。
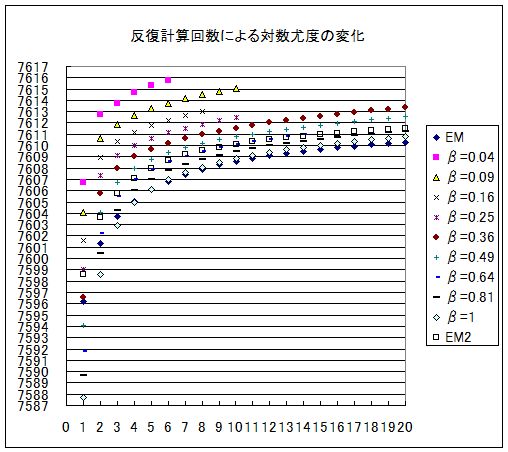
βを大きく採って、比較の為の対数尤度も大きめに採って比較した。下図は対数尤度≒7609とした場合の比較である。
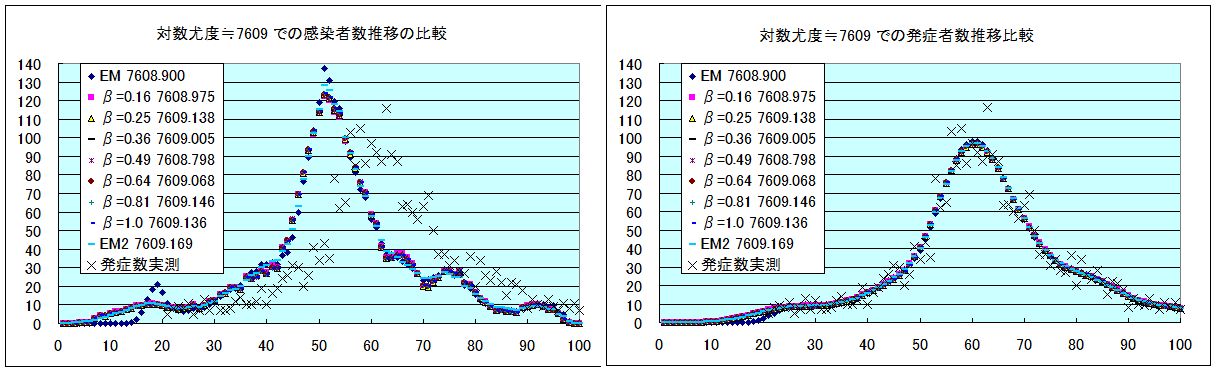
こうなると、EM法との違いは19日近傍のピークだけである。僕の EM法のプログラムがおかしいのかもしれないので、統計言語 R に登録されているライブラリー surveillance の中のプログラム backprojNP で EM 法の計算をしてみた。実例に沿って、データだけを変更して計算した。フィルターは無しである。設定どおりの収束条件で 32回反復したので、更に起伏が激しくなっている。僕の EM法のFORTRANプログラムでも同じ回数で計算して全く同じ結果になったので、プログラムに間違いはないだろう。下記には設定どおりの R での作図を示す。棒グラフが観測発症数、青線が推定感染者数、緑線が推定発症者数である。
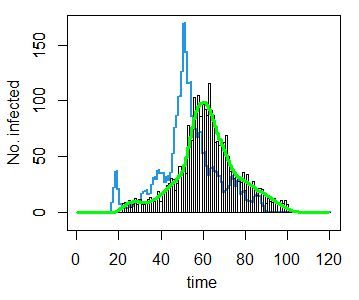
なお、R でのプログラムには続きがあって、信頼区間を算出している。 これは、EM法そのものに拠るのではなく、観測データから疑似的に作り出した1000個程度の観測データ(ブートストラップ法)から、同じように発症日推移を計算して、その振れ幅を出している。相当な計算量になると思われるのでやっていない。これは、観測データの信頼性に由来する信頼区間である。(Cori 等の実効再生産数の信頼区間もそうであった。)そもそも尤度最大の解に現実的な意味が無いのだから、尤度に基づく信頼区間は算出しようもないのである。
●EM法の改訂版 EM2法
計算の間違いではないようなので、原因を考えてみた。最初から気になっていたのだが、観測データが始まる以前のデータをどう扱っているのか?である。
潜伏期間分布が 1日後から L 日後まで分布しているとする。f(0)=0, f(d>L)=0 である。
また、観測データが M 日あるとすると、推定すべき感染日は、その L 日前からであるから、その L 日間は発症者数データが無い。
t=1~T、とすると、λt としては、感染当日の発症が無いので、1 ~ T-1、発症者数データは L+1~T となり、T=M+L である。
F*(T-t)=∑(d=0~T-t) f(d)Y(t+d)/Y*(t+d)
という式において、和の中身が正となるのは、0<d≦L、且つ、L<t+d≦T の場合である。後者は観測データが無いので、0 とされているからである。
つまり、max(0,L-t)<d≦min(L,T-t) である。ところが、
F(T-t)=∑(d=0~T-t) f(d)
という式においては、和の中身が正となるのは、0<d≦min(L,T-t) である。
つまり、F*(T-t)/F(T-t) において、分母の和の範囲は、t<L においては、分子の和よりも広くなっている。EM法の趣旨はまだ理解していないのだが、推定発症者数と観測発症者数との比率を関係すべき感染日での感染者数の影響を考慮して、潜伏期間分布で期待値を採ってから、その感染日の感染者数補正に使う、という趣旨であるとすれば、分母と分子は同じ範囲の和とすべきである。
そうすると、F(T-t)は、t<L において、∑(d=L-t~L)f(d) となり、T-t<L において、∑(d=1~T-t)とすべきではないか?その中間では 1 になる。
実際そうしてみたら、始まりの部分のピークが消えて、対数尤度も大きくなった。非線形最小自乗法と変わらなくなった。 これが 上のグラフのEM2 の場合である。
これは、必ずしも EM法が間違いだという事ではない。観測発症者数データが無い、それ以前の期間については発症者数=0 として計算している、ということに過ぎない。従って、アウトブレイクの最初から計算する場合には何の問題もない。途中からのデータで解析するときにはその事による疑似的なピークが生じてしまうので、注意が必要である 、という事に過ぎない。それを避ける為には EM2 法で計算すればよい。そして、これは非線形最小自乗法でも出来る。
なお、確認の為に、観測データの前20日間に小さな発症者数(0.1人とした。計算上、最初のデータを 0 には出来ない。)を追加して非線形最小自乗法で計算すると、EM法と同じ初期ピークが出現した。