2021.01.24（01.30：記号を統一、シミュレーション追加、考察追加。02.07：消滅確率の考察追加）
・・・序・・・
       Superspreader の論文（Lloid-Smith）。SARSを経験して得られた感染症疫学の重要な成果と見なされており、その意味で必読文献である。西浦氏が日本でのCOVID-19対策としてクラスター対策に集中したときの根拠となった。COVID-19についての確率モデルの論文（Hellewell et al.）で引用されていた論文である。"Superspreading and the effect of individual variation on disease emergence", J.O.Loid-Smith et al. doi:10.1038/Nature04153,vol.438(17)pp.355-359(2005)。同じ内容のpreprintとして、下記もあちこちに見つかる。"Superspreading and the impact of individual variation on disease emergence"。

      苦労した。supplemental information を読まないと良く判らない。再生産数は原理的には全ての感染事象を観察出来れば具体的に求められる。通常は個々の一次感染者が何名に感染させたかを調べて、その平均を採れば良い。この平均ではなくこの分布についての論文である。SARSの流行時に問題となり、そのデータを解析している。（今回のCOVID-19についてはまだデータが揃っていないと思われるが、ほぼSARSに近いのではないかと言われている。）個々の二次感染者数は確率的に現れた事象であるとすると、平均としてはある再生産数であるようなポワッソン分布と見なされる。この個人平均としての再生産数というパラメータ（ν：ギリシャ文字ニュー）がその一次感染者固有のものだとする。更に、この個別平均再生産数（ν）がどんな分布をしているか、について仮定をおいてデータと比較する。なぜこのように確率分布を二重に考えるのか、というと、「感染させるーさせない」という事象はどう考えてもポワッソン分布なのに、実際のデータがそうなっていないからである。

・・・考え方・・・
モデル（１）
      ν の分布が無くて単一の値、つまり全平均としての再生産数 R0 であるとすると、観測される二次感染者数の分布は z 〜ポワッソン分布になる。この場合に即してポワッソン分布を定義すると、z〜(r^z)exp(-r)/z!：r= R0/感染可能期間、ということになるが、感染可能期間は問わないので 1 とすればよい。z の期待値は当然 R0である。

モデル（２）
      ν の分布が指数関数的であるとすると、その形は（平均が R0 だから）ν 〜exp(-ν/R0) である。この時には二次感染者数の分布は z 〜幾何分布（z,1/(1+R0))になる。なお、幾何分布(z,p)= p(1-p)^(z-1)である。ν の分布が感染可能期間の分布と同じであるとすれば、これはちょうど感染力が指数関数的に減衰するというモデル、つまり S(E)I(Q)R モデルで採用された感染力プロファイル〜exp(-γt)に相当する。ただし、S(E)I(Q)R モデルそのものは決定論的微分方程式であるから、νの短い方から順に実現するのに対して、ここではランダムに選択されている。

モデル（３）
      実際の分布はこれらの中間と思われる。そこで、著者は ν の分布としてガンマ分布を想定している。期待値が R0で 異方性が k である。分布形は、ν 〜ガンマ分布(ν,k,k/R0)＝{(k/R0)^k/Γ(k)}ν^(k-1)exp(-(k/R0)ν) である。k= 1 とすると（２）になり、k=∞ とすると（１）になる。（R0= 1.5として、いろいろなk についてのガンマ分布は表の次の図aにある。）この時、二次感染者の分布は z 〜負の二項分布(z,k,1/(1+R0/k)) になる。このモデルだけが余分にパラメータ k を持っているので、実態に合わせて決めることができる。なお、負の二項分布は、成功確率を p として、k回の失敗をする前に成功した試行回数z の分布(z,k,p)= C(z+k-1;z)(p^k)(1-p)^z で、k を非整数まで拡張すると、{Γ(z+k)/z!Γ(k)}(p^k)(1-p)^z 、z の期待値＝k(1-p)/p＝R0とすれば、p が決まる。k= 1では幾何分布、k= ∞ではポワッソン分布。負の二項分布にはいろいろな定義があるので紛らわしい。ここでは統計言語 R での定義を使った。z の分散は k(1-p)/p^2 ＝R0(1+R0/k) である。負の二項分布には再生性がある。つまり、独立な確率変数がそれぞれ負の二項分布に従うときにはそれらの和も異方性パラメータを加えた二項分布に従う。従って、n人の一次感染者が生み出す二次感染者数の従う分布は期待値 nR0で、異方性nk の負の二項分布である。n が増えればこれはポワッソン分布に漸近する。なお、ガンマ分布とポワッソン分布と負の二項分布の関係については、下記に判りやすい解説がある。
可視化で理解する「負の二項分布」 - ほくそ笑む (hatenablog.com) 

・・・論文の結果・・・
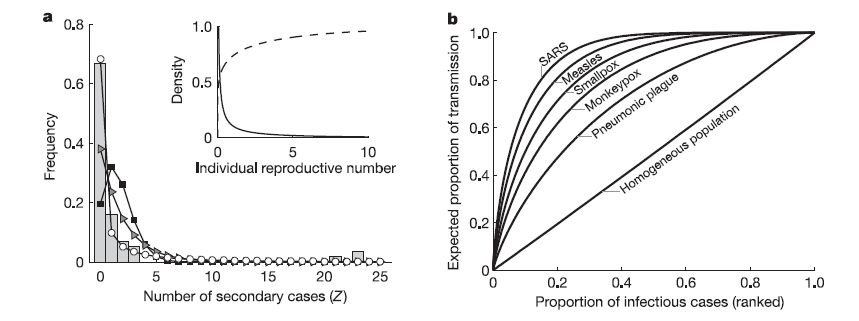
      最尤法で異方性パラメータ k を推定するときに、α=1/k について最適化する。更に重要なことであるが、k<1 の領域も調べる。ということは（３）は（１）と（２）の中間ということではなくて、（２）よりも更に異方性の大きい場合を含むということである。実際 SARSの場合にそうなっている。下図aがそうである。■が（１）、▷が（２）、○が（３）である。
異方性を判りやすく表示する為に、一次感染者のどれ位の割合が二次感染者のどれ位の割合を発生させているか、というグラフを描いている。これは所得格差を表現するローレンツ曲線と同じで、（１）の時に直線となり、感染能力の偏りが大きいほど直線から外れる。下図b。

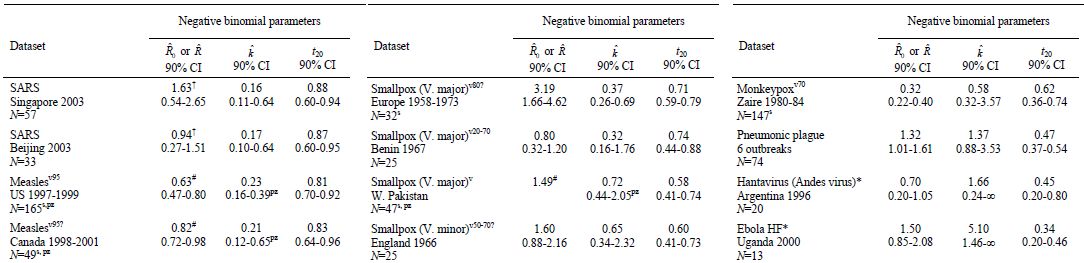
具体的に各ケースでの最適パラメータはSupplementary Tableにある。

      SSE(Super spreading event) の定義を提案。まずモデル（１）によって二次感染者数についてのポワッソン分布を確定する。その例えば99%範囲を超えるような二次感染者数を与えた一次感染者を super spreader と定義する。

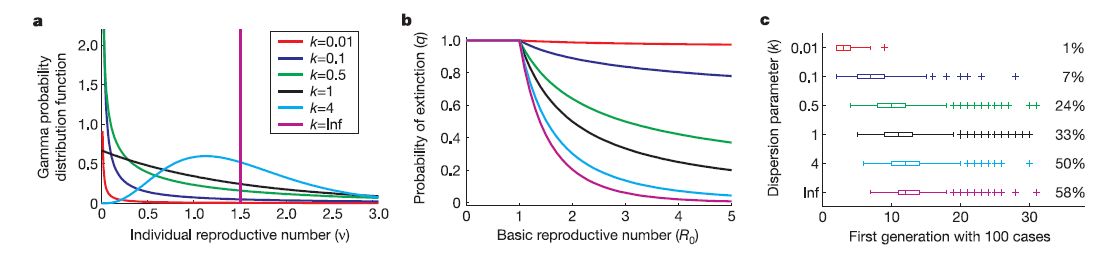
     このような感染能力の偏在がある場合に、感染状況にどのような影響を与えるであろうか？S(E)I(Q)Rモデルのような計算方法とどこが違ってくるだろうか？Branching Process Model という概念が必要である。全人口の中に一人の一次感染者を入れた時（あるいは残された時）を初期状態として想定する。S(E)I(Q)Rモデルでは、平均としての再生産数（β/(γ+q)）が１を超えれば感染が拡大し、１を下回れば終息する。終息の場合は感染者数が１人以下という計算になって、決して 0 にはならないから、もうその辺で明らかな限界であるが、解釈として 0 になったとするしかないだろう。下図aのような異方性を想定して、ポワッソン分布を使って確率計算をすると、再生産数が１を超えていても感染者数が 0 になる確率（消滅確率）q がゼロにはならない。これは異方性が大きい（kが小さい）ほど大きい（下図b）。逆に、感染が拡大していく場合についても、異方性の影響が顕著である。異方性が大きい場合には、感染者が例えば100倍になるまでの感染世代数が少ない（下図c）。つまり、感染拡大が早いが、その比率は低い。つまり、たまたま super spreader であった場合には急激に拡大するが、そうでない場合は消滅してしまう。こういうのを Overdispersion 効果というらしい。R0 は 1 を超えていてもその分布が広いので、大部分のケースでは １以下になって、感染爆発に至らないということである。（ワクチンによる終息効果も高くなると思われる。）

     感染対策を人口全体に対して均一に実行する場合と、ランダムに選択した人を徹底的に隔離する場合を比較する。いずれも平均としての再生産数の低減は同じであるとする。後者の方が再生産数のバラつきを大きくするから、感染終息には有効である。しかし、他方で super spreader を見逃す可能性もある。もしも、super spreader をうまく見つけて隔離できれば極めて効率的である。

・・・理解の為のシミュレーション・・・
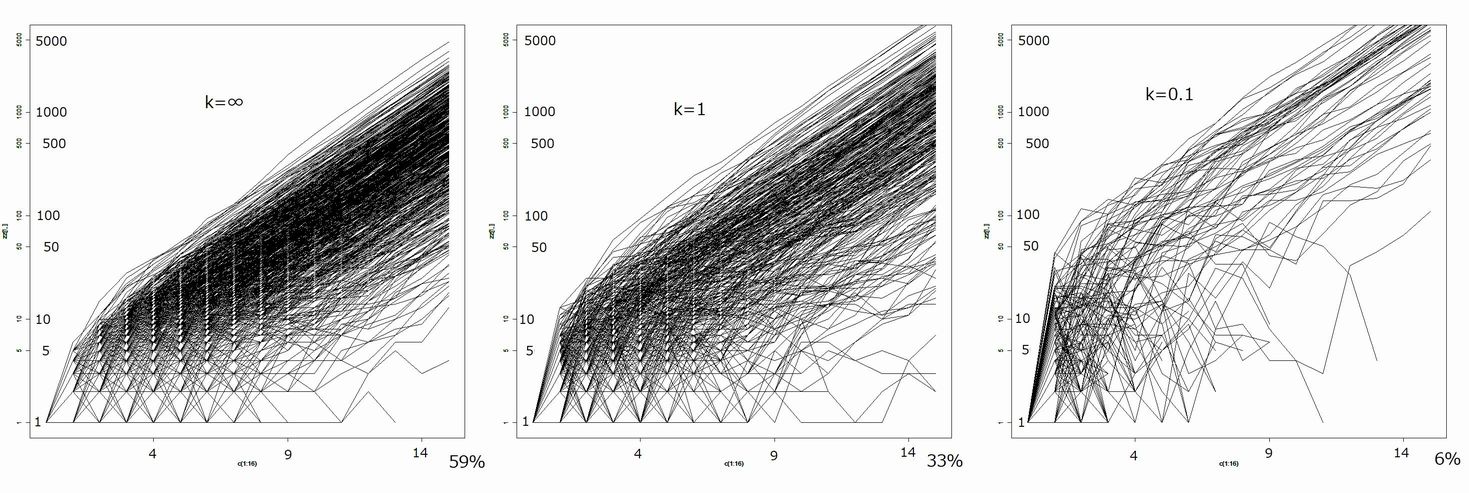
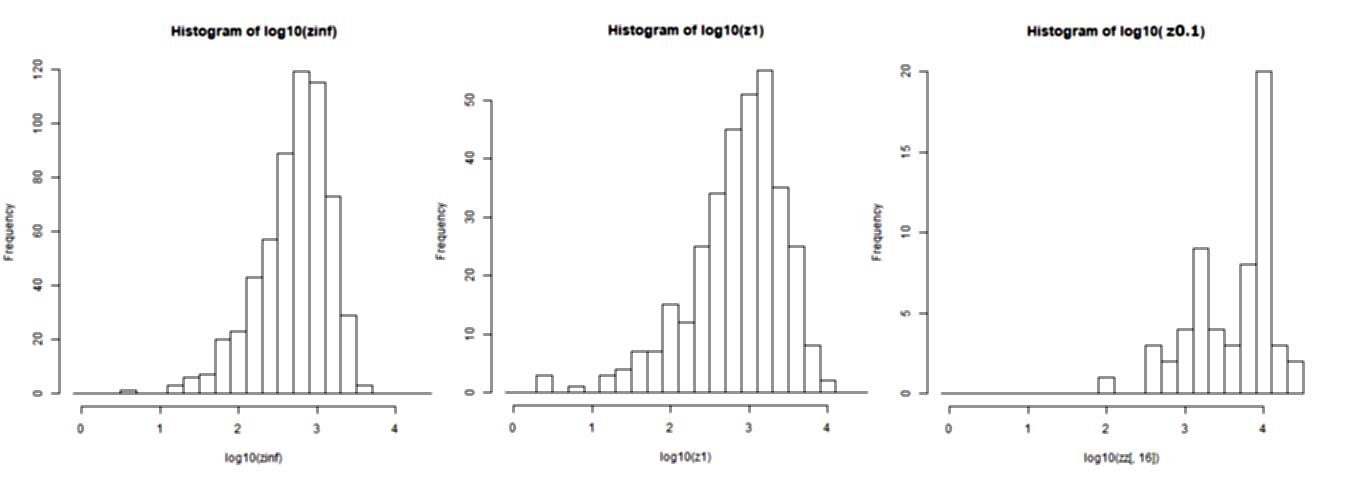
      なかなかイメージが掴めないので、計算してみた。初期条件は感染者一人である。R0=1.5 として、k＝∞、k=1、k＝0.1 の場合、15世代に亘って感染者数がどう変化するかを計算した。（一世代というのはほぼ一次感染者と二次感染者の平均的な感染時間間隔であり、COVID-19では５〜６日位である。）確率的な計算なので、1000回繰り返した。下図、一本の線が一回の計算である。概ね感染者が10〜100人を超えると直線になるので、S(E)I(Q)Rモデルのような決定論的な微分方程式が良い近似解法になると思われる。線が途切れている処は感染者が居なくなった場合である。%というのは、生き残ったケースの割合であり、実際に我々が感染爆発として問題としているのはその生き残った場合だけである。15回目での感染者数の対数分布グラフも示した。分布形は似たような処に落ち着くが、k が小さい場合には対数平均が大きい。（k= 0.1で二つピークがあるように見えるのは確率的な揺らぎである。）勿論普通の平均はどれも同じで、約R0＝1.5の15乗になっているので、kが小さい場合には 0人（対数を取ると-∞）の割合が多くて、それを頂点としてなだらかに下がる分布の裾野が広いということである。

      COVID-19の場合として、k= 0.1 を見る。感染者を一人づつ全国にばらまいたとする。最初の感染で23%しか残らない。しかも10人以上が多い。これがクラスターである。このようなケースを徹底的に潰していく。二次感染者が一人の場合はその次の世代でまた同様な事が起きるが、最初の1000人に比べれば10数人となっているので、これを繰り返せば感染爆発が抑え込める。これがクラスター対策の考え方である。k= ∞の場合は感染者が広く浅く出現するのでこのような対策が難しい。



・・・私的考察・・・
        Lloid-Smith の解析モデルは、一次感染者個人が何人に感染させる能力があるか、という個人的再生産数 ν を持ち、しかもそれが実現するかどうかはベルヌーイプロセス、つまりお神籤を引いて吉か凶かを占うようなものである、という事である。しかし、これら二つの事象の原因と想定されるものは明確ではない。むしろ想定可能な原因全てを個人的再生産数 ν に割り当てて、それ以外の偶然的なプロセスをベルヌーイプロセスとしてモデル化した、という事だろう。原因として考えられるものであるが、基本的にはウイルスの発出量があり、これは病態とか治療だけでなく、その人がお喋りかどうか、とかマスクをしているかとか、といった本質的に個人の特性である。しかし、それだけでなく、未感染者とどれ位の接触があったか、という感染者ー被感染者の両方に絡む原因とか、逆に、被感染者がどれ位ウイルスに感受性があるかとか、どの程度注意をしていたか、という被感染者側の原因も νのバラツキに寄与しており、更にこれらは行動制限や検査・隔離といった社会政策にも影響される。こういった、ありとあらゆる原因によって ν とそのバラツキパラメータ k が決まっていて、それでも感染するかどうかには偶然性が残る。そもそも感染したかどうか、というのは閾値現象として曖昧さが無いのであるから、それでも残る偶然性を記述するのはベルヌーイプロセスだろうということで、そのパラメータが ν とされた。

        一次感染者が感染させた二次感染者の数が多数の一次感染者について判っている場合には、それらの数の分布が得られる。もしも二次感染者数分布がポワッソン分布であれば、ν には分布が無くて、そのポワッソン分布のパラメータが再生産数 R として確定するが、分布があれば、その平均値が再生産数として決まる。ν の分布をガンマ分布とすれば、二次感染者数の分布は負の二項分布になるので、この分布形で観測された二次感染者数の分布を表現できれば、ν の分布が得られる。このモデルのもう一つの特徴は、二次感染者数の分布がポワッソン分布よりも狭くなることは原理的にあり得ないということである。

        ポワッソン分布というのは、生起確率の極めて低い事象を引き起こす試みが多数回行われた時に、その事象が何回起きるか、という確率分布である。パラメータはその生起確率×試行回数=平均の生起事象数である。従って、ある条件を満たす接触があれば相当高い確率で感染させるというような感染症には当てはまらない場合が多い筈である。そのような場合には接触回数がそのまま個人的再生産数となるが、二次感染者数の分布はその分布に近いものとなり、極めて規則的な生活を強要されている集団においてはポワッソン分布よりも狭くなり得る。しかし、実際に過去の感染症を調べるとそのような事にはなっていない、というのがこの論文のもう一つの側面である。逆に言えば、感染確率が１に近いような接触状況を同定することができない、という事も意味している。

       もう一つ、この考えの面白い処は発症とは関係無いことである。つまり、発症というのは病態がある閾値を超える場合を指すだけであって、そういう意味では、不顕性感染者に対するモデルを考える上で参考になるかもしれない。

       （追加情報） COVID-19については、次の論文が見つかった。 F.Wong et al.,"Evidence that coronavirus superspreading is fat-tailed",PNAS,vol.117,no.47(November 24,2020),https://www.pnas.org/content/117/47/29416。どういう分析をしたのかまだ良く判らないが、COVID-19 では負の二項分布よりも分布の裾が長いそうである。負の二項分布は、k<1では、指数関数的な裾だそうだが、実際の分布は べき乗的な裾だそうである。ベキは-1〜-2。分布そのものは パレート分布で近似できる。この分布の元となるのは ν の分布というよりも、感染間隔（generation time）の分布だそうである。それが、ガンマ分布であることからくる。この辺の理屈もまだよく判らない。引用文献に中国外初期と香港での SSE 事例の報告があった。

・・・消滅確率についての計算・・・
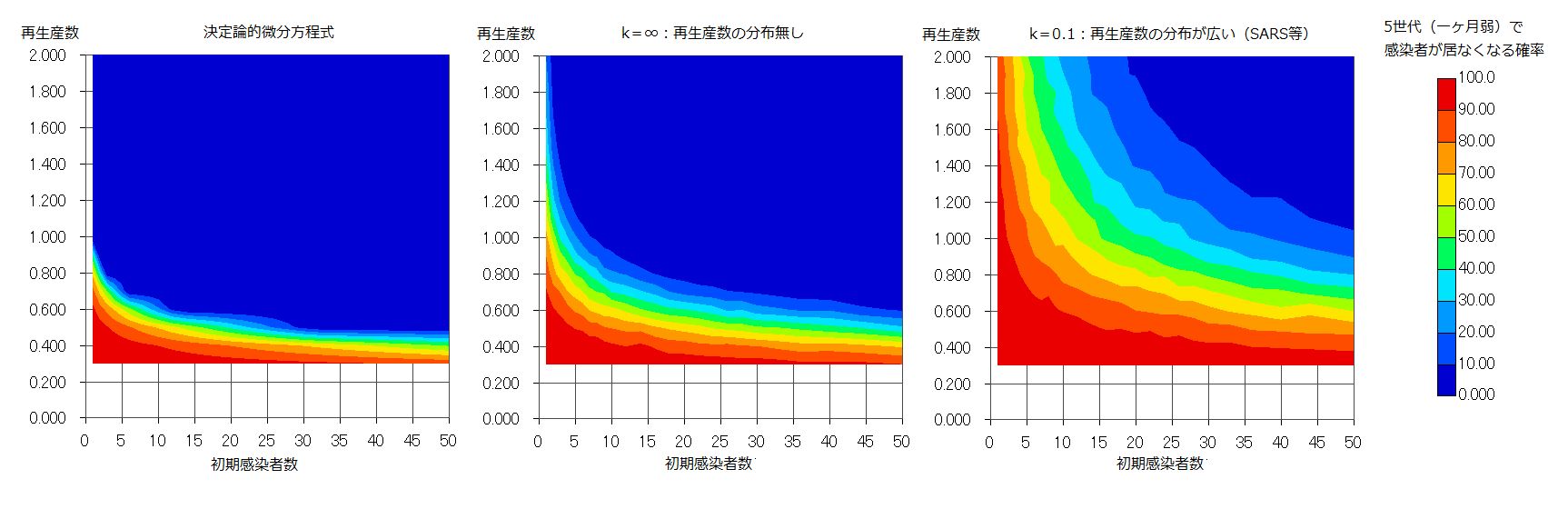
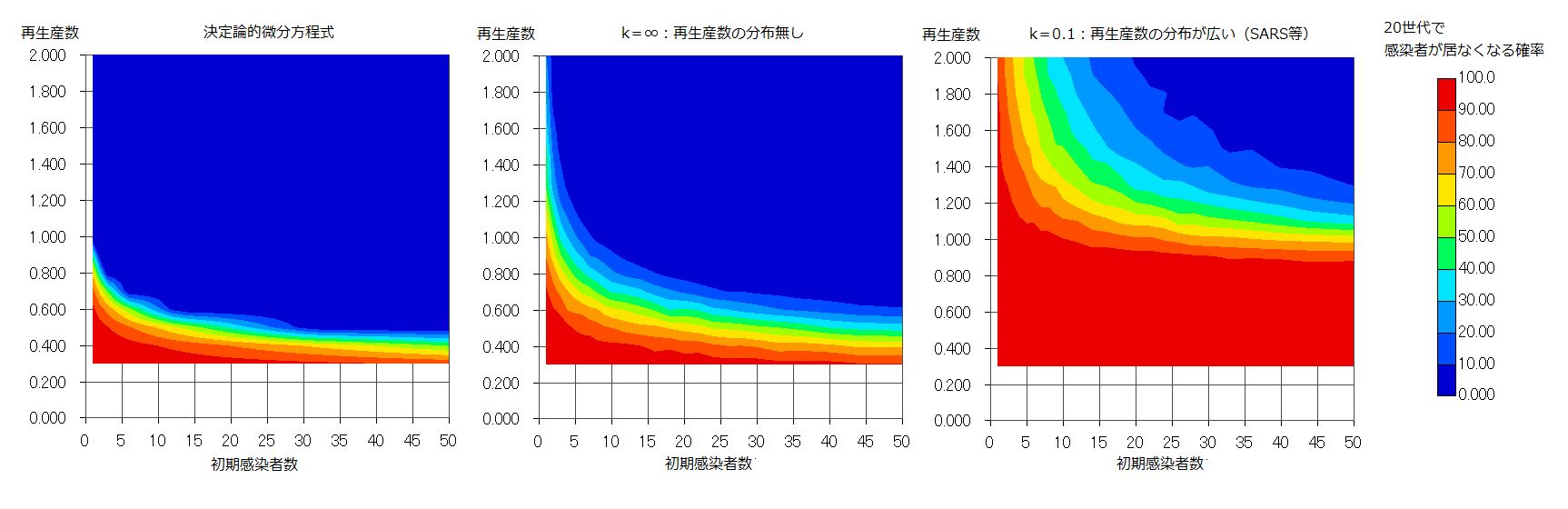
        シミュレーションによって、k=0.1 程度の大きな再生産数の分散がある場合にも 感染者数 100人以上であれば、決定論的微分方程式で感染拡大が記述できることが判った。それ以下の場合は確率的に取り扱って計算した方が正確な把握が出来る。とりわけ重要なのは、どれ位の感染者数に達すれば感染が完全に終息（感染者 0 ）するのか、という事である。これは、そこから何世代かの感染プロセスを経た後に、感染者が 0 になる確率がどうなるか？という形式でしか答えられない。 世代数を無限大にした場合の答えは Lloid-Smith の論文の図b にある通りであるが、実際には有限の世代数が問題になるので、再生産数が 1 以下でも完全消滅までは行かない場合が生じる。そこで、5世代（一ヶ月弱）と20世代について計算してみた。比較としては、k＝無限大（再生産数の分散が無い）の場合の他に、決定論的微分方程式の場合も計算した。ただし、この場合感染者数が整数にならない。1 人以下になれば、消滅として解釈してもよいだろうが、ここでは 1 人以下の場合には１からその数を引いた確率で消滅すると解釈する。つまり 0.3 人になれば、消滅確率を 0.7 と解釈する。結果を分布図で示した。感染対策を厳しくして感染者数を少なくしている時には再生産数 Re は 1 以下であるが、どこかで対策を緩めれば 1 を超える。Re＝１まで緩めた状態を一ヶ月続けて、感染者が居なくなる確率を 0.9 にするには、2人以下にしなくてはならない。４ヶ月 Re＝１を維持するつもりならば、10人以下で大丈夫である。


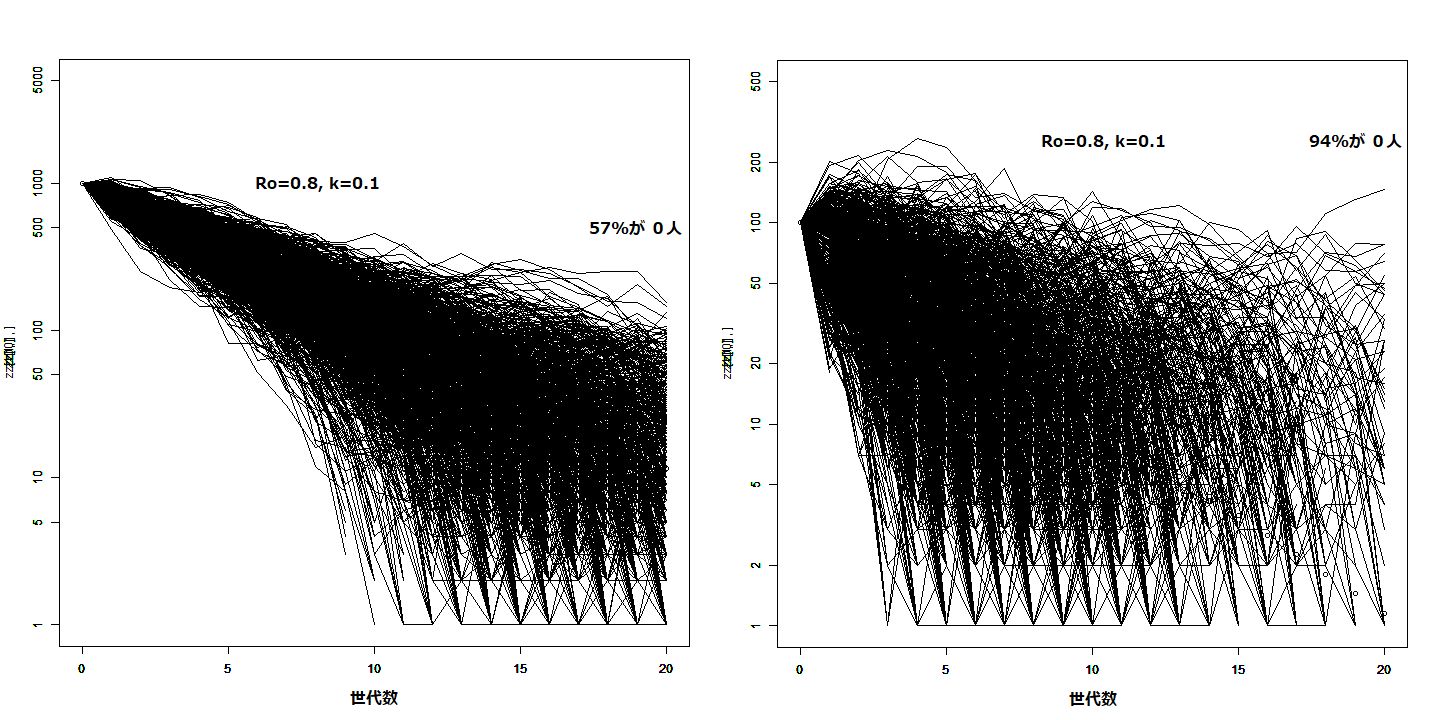
感染者数が100人以下になってくると、決定論的微分方程式予測することが難しくなる。再生産数＝0.8、分散パラメータ k=0.1の場合での、初期感染者数＝1000人と、100人の場合で、20世代確率計算（1000回計算）したものである。一本の線がそれぞれ実現可能な感染者数の推移を表す。100人程度までであれば、指数関数的減衰（○印）で近似できそうであるが、それ以下になると、予測幅が広くなりすぎる。