K17.暑熱環境と黒球温度
著者:近藤純正
17.1 はしがき
17.2 湿球黒球温度 WBGT
17.3 湿球黒球温度の問題点
17.4 晴天日の日射量の計算
17.5 黒球温度の計算
17.6 黒球温度の諸条件への依存性
(ⅰ)黒球温度と風速及び直径との関係
(ⅱ)支柱からの熱損失などの影響
17.7 自然湿球温度(WBGT 計算用)のあいまいさ
要約
参考文献
太陽の直射が注ぐ極暑の条件下における労働やスポーツ時の高温環境を
評価するために、近年、黒球温度を用いた温熱指数(暑熱指標)が提案
されている。その一つの指標としてWBGT
(Wet-Bulb Globe Temperature: 湿球黒球温度)がある。市販の測定器に
よって現実に測られる気温、自然湿球温度、黒球温度には曖昧さがあるために、
それらをもとに計算される WBGT には数℃の誤差が生じる。
この章では黒球温度がその直径や気象条件によって変わることを
理論的に考察する。また、現在、推奨されている自然湿球温度
(日射に暴露した状態で測る湿球温度)を用いるのではなくて、通風式
乾湿計で測る湿球温度を標準値として用いることを提案する。
現実的には、湿球温度は最近の湿度センサーで測った水蒸気量から換算して
求められる。この方式では、湿球温度は放射を受けない状態の値であるので、
温熱指数の基準値(高温許容基準)は少し変わることになる。
(2006年4月12日完成予定)
17.1 はしがき
快適さや不快さは、人体と周辺環境との間の熱収支によって決まる。
軽作業の人体は日平均値として単位面積1m2
当たり、およそ100W/m2 の熱を放出することで体温が正常に
保たれている。適度な熱放出は着衣によって調節されている。
熱放出は赤外放射、顕熱、発汗による潜熱の3成分からなる。これら熱
放出量の大きさは気温、湿度、風速、人体の皮膚温度に依存する。
人体内部で発生する代謝熱が皮膚から放出されるわけだが、
周辺環境の温度が高いときや強い放射を受ける状態では、正味の
熱放出量が少なくなり、暑いと感じる。
この章を考えることになったのは、ある地域に工場が建設されることになり、
その外壁が高温になるということで、付近の住民がその高温放射によって
影響を受けるようになる、ということを聞いたことが研究の動機である。
17.2 湿球黒球温度 WBGT
近年、スポーツや労働環境において作業者が受ける暑熱環境による熱ストレス
の評価を行う簡便な指標としてWBGT(Wet-Bulb Globe temperature:湿球黒球
温度:単位は℃)が使われるようになった。
例えば、厚生労働省労働基準局安全衛生部長による通達「熱中症の予防対策
におけるWBGTの活用について」基安発第0729001号、平成17年7月29日によれ
ば、熱中症による死亡者数は毎年20人前後あり、熱中症の予防対策において、
暑熱環境のリスクを評価する指標としてWBGTの活用を勧めている
(厚生労働省のホームページ、労働基準情報)。
例えば上記によれば、WBGT は自然湿球温度と気温と黒球温度を測定し、
次式によって計算する。
(1)屋内及び屋外で太陽照射のない場合
WBGT=0.7×自然湿球温度+0.3×黒球温度・・・・・・・・・・
・・・・・・・・・(1)
(2)屋外で太陽照射のある場合
WBGT=0.7×自然湿球温度+0.2×黒球温度+0.1×気温・・・
・・・・(2)
ここに、自然湿球温度とは「強制通風すること
なく、輻射(放射)熱を防ぐための球部の囲いをしない環境に置かれた
濡れガーゼで覆った温度計が示す温度」である。つまり、家庭用として
使われている非通風式乾湿計(例えば、August 温度計)をそのまま野外へ
持ち出して測った湿球温度であり、実際の湿球温度(アスマン通風乾湿計
の湿球温度)より、日中なら数℃高温の値となる。
黒球温度とは、
「直径が150mm、平均放射率が0.95(つや消し黒色球)、球殻の
肉厚ができるだけ薄い、中空黒球の中心に位置する温度計の示す温度」
と定義されている。
WBGT の測定を行うために、作業現場で自然湿球温度、気温、黒球温度
の3つを測る携帯用の測定器も市販されている。WBGT を自動的に計算する
黒球の測定機器も市販されている。
日本工業規格 Z 8504「人間工学ーWBGT指数に基づく作業者の熱ストレスの
評価ー熱暑環境」付属書 A に基づく基準値表があり、この基準値を越えた
場合には熱中症が発生するリスクが高まったと考えるようになっている。
日本産業衛生学会が提唱している高温の許容基準によれば、
WBGT=32.5℃・・・・・極軽作業
WBGT=30.5℃・・・・・軽作業
WBGT=29.0℃・・・・・中程度作業
WBGT=27.5℃・・・・・強作業
WBGT=26.5℃・・・・・重作業
(財)日本体育教会資料の熱中症予防のための指標 WBGT によれば、
WBGT>31℃・・・・・・特別の場合以外は、運動を中止する。
28~31℃・・・・・・・・・激しい運動や持久走など熱付加の運動は避ける。
25~28℃・・・・・・・・・積極的に休憩し、水分補給する。
21~25℃・・・・・・・・・熱中症の危険は小さいが、適宜、水を飲む。
WBGT>31℃は、それを計算しないときの目安として、湿球温度>27℃、
または気温>35℃で代用する。
市販されている黒球として次の例がある。
直径=150mm(6インチ)・・・・・基準とされている
直径=75mm(3インチ)
直径=50mm
直径=24mm(1インチ)・・・・・ハンディタイプ
小さい直径の黒球で測った温度を直径150mmの場合に換算して利用する
市販品もあるが、換算方法はあいまいである。
もともと WBGT は Yaglou and Minard (1957) により提唱されたようであるが、
彼らの論文では、乾球温度と湿球温度は直射光を防いだ
"slig psychrometers" で観測している。これは乾湿計を鎖か棒の端に取り
付け、その手元をもってぐるぐると振り回し、実質的な通風を行うことで
気温と湿球温度を観測する方法である。アスマン通風乾湿計による気温と
湿球温度にほとんど等しい値が得られる。
これが、いつの間にか、放射場に暴露状態にして測った「自然湿球温度」を
WBGT の計算に使うようになったか、筆者はその経緯について現在のところ
知らない。
17.3 湿球黒球温度の問題点
(1)黒球の標準は、直径=150mmのものとなっているが、現実には
携帯上の便利さその他の理由により、それよりも小さい黒球が使用される
ことが多い。その場合、実測の黒球温度を自動的に大きい直径の黒球温度
に換算する機種もある。通常、現場の風速は測定していないので、野外では
風速=3m/s=一定 として自動的計算回路が組み込まれていると聞く。
のちほど示すように、風速一定の仮定と、換算式の曖昧さから、自然湿球温度
には数℃の違いが生じる。
(2)WBGT 計算式に用いる自然湿球温度と
して、現実にはいろいろなサイズの湿球温度計が用いられている。直射光
のもとで示す温度は標準的な自然湿球温度(放射除けなし)と比べて
風速と温度計の設置方法によって数℃も違う。
太陽の方位によって絶えず温度計の向きを調節する作業は行われている
だろうか? つまり、現場では湿球温度は日射や自然風の当たり方によって
著しく変化するのだ。
古くから常用されてきた板付きの乾湿計は屋内での設置は簡単だが、屋外
では、最近の傾向として、例えば小さいサーミスター・センサーで気温を、
湿度センサーで相対湿度を測ることが多くなっている。この場合には、
気温と相対湿度から湿球温度計(棒状温度計、球部の直径=9mm、
無通風のフース型)の温度を逆算して利用することもあるという。
最近の気象観測では、無通風のフース型温度計は一般には使用されなく
なったが、この温度への正確な換算は複雑で温度や相対湿度、さらに放射
条件の複雑な関数となる(Kondo, 1967)。それゆえ、換算された自然湿球温度には数℃の誤差を含む可能性がある。
熱中症による死亡事故などが発生し、裁判沙汰となるような場合に、
これら(1)、(2)が深刻な問題となりそうである。
記憶は定かではないが、1990年の頃、徳島県のある中学校で運動中の生徒
が熱中症で死亡する事件があり、父母側は学校側に責任があるとして裁判
となり、最高裁判所まで上告したが、結果は父母側の敗訴となった。
最高裁判所に上告中の2000年の頃に、事件当時の気象条件を推定する方法
について相談されたことがある。しかし、推定するために必要な資料を
得る目的の現地調査する前に敗訴が決まってしまった。
これらの事故・事件が多発するようになってから、労働・スポーツ分野で
WBGTが活用されるようになってきたと思われる。近年、計器による測定値
が重視される風潮にあることは困るが、他方では WBGT の
値の曖昧さの度合いを明確にしておく必要がある。
曖昧な WBGT の数値に頼ることなく、現場での監督、責任者は労働・スポーツ
する人々の訴える暑熱感覚を聞き入れ、また自らもその環境で暑熱感覚を体験
して、事故・事件の防止対策をとることが大切である。人体そのものが
もっとも正しい暑熱指数計である。
この章では、WBGT に用いられる黒球温度とはどういうものか、
その直径や風速等の条件による振る舞いを検討しよう。また、その結果から
黒球温度の実験・観測データの整理の指針を示したい。
なお、WBGT の計算式の見直しは今後の課題となる。
17.4 晴天日の日射量の計算
次節で説明するように、地上に置かれた黒球の温度は球表面における熱収支
によって決まる。通常の平面上の熱収支と違って、球面上では直達光と散乱光
の各成分を考慮して計算される有効入力放射量(R↓-σT4)
がパラメータとなる。
そこで、この節では、(1)直達日射量 I、(2)散乱日射量 Sd、(3)大気放射量 Ld、
(4)地面からの反射光 Su、(5)地面からの赤外放射量 Lu の計算を行う。
これらは次節における黒球温度を計算する際に、球面に入る放射量R↓の
試験データとして用いる。
試験データを作成するために次の条件を設定する。
(1)夏の条件:
8月1日(day=214)、北緯35.5°、快晴、日平均気温=30℃、日平均水蒸気圧=25hPa、
大気の混濁係数=0.1、周辺数km範囲のアルベド REF=0.2とする。
このアルベドは、日射が地表面で上空に向けて反射し、それが大気中で散乱
されて地表面へ再び入射する散乱光を与えるのに必要なパラメータである。
地表面へ入射する散乱光は太陽直達光が大気で散乱されてくる成分と、
地表面アルベドによって決まる成分を含んでいる。
(2)秋の条件:
10月1日(day=275)、日平均気温=20℃、日平均水蒸気圧=15HPa、大気の混濁係数
=0.05、その他は夏の条件に同じ。
(3)年平均的条件:
曇天日も含む。日平均気温=15℃、放射量の諸成分は表17.1の最後の
列に示す。この数値は、計算値ではなく、日本の代表として与えたものである。
なお、この地表面アルベド REF と黒球のアルベド REFB は区別する
(特に明示しない限り、黒球は黒体、そのアルベドは REFB=0とする)。
日射量の計算
日射量の日変化の計算プログラムは「地表面に近い大気の科学」の付録 E に
掲載されている。
クリックして次の
「晴天日の放射量の日変化の計算」を参照し、プラウザの「戻る」を
押してもどってください。
上記の設定条件から計算された放射量の諸成分は表17.1に示した。
表17.1 放射量の諸成分(単位は W/m2)、
気温、地表面温度および水蒸気圧の表
気温と地表面温度の単位は℃、水蒸気圧の単位はhPa、時刻は地方時。
有効入力放射量はR↓-σT4、σT4は気温 T に対
する黒体放射量である。
夏 夏 夏 秋 秋 秋 年
12時 14時 16時 12時 14時 16時 雲あり
① ② ③ ④ ⑤ ⑥ ⑦
入力放射データ
直達日射量 I 803 776 665 889 852 676 100
散 乱 光 Sd 84 80 66 50 47 35 70
大気放射量 Ld 412 412 412 334 334 334 330
地面反射光 Su 172 150 89 150 125 58 30
地面赤外放射 Lu 658 658 619 546 546 479 402
黒球の単位面積に入る放射量[(I/4) + (Sd+Ld+Su+Lu)/2]
入力放射量 R↓ 864 844 759 762 739 622 441
有効入力放射量 385 365 280 343 320 203 50
参考値(S)と入力データ(Ts,T, Vp)
水平面日射量 S 852 742 444 750 625 291 150
気温の黒体放射量 479 479 479 419 419 419 391
地表面温度 Ts 55 55 50 40 40 30 17
気温 T 30 30 30 20 20 20 15
水蒸気圧 Vp 25 25 25 15 15 15 10
17.5 黒球温度の計算
前節の表17.1で求めた入力放射データを用いて黒球温度を計算する。
黒球は熱伝導のよい金属で作られており、その温度は一様分布であるとする。
球から出て行く顕熱と赤外放射は、球の半径を r とすれば全表面積
4πr2 から放散されるのに対して、直達光 I は球の
断面積 πr2 に入射し、その他の成分(Sd、Ld、Su、Lu)は
半球の面積 2πr2 に入る。
簡単化のために、散乱光(天空光)などその他の成分は方向によらず
一様分布と仮定すれば、球の単位面積当たり
に入る放射成分は次式で表される。
R↓=I/4 +(Sd+Ld+Su+Lu)/2・・・・・・・・・・・・・(3)
気温に対する黒体放射量との差:R↓-σT4・・・・・(4)
は有効入力放射量(水環境の気象学、p.133;地表面に近い大気の
科学、p.40)と呼ばれ、黒球の温度上昇(⊿T=黒球温度-気温)とその正負
を決める重要なパラメータとなる。
黒球の温度を Tb とすれば、熱収支式は次のように表される。
入力放射-赤外放射-顕熱-潜熱=0
(R↓ - σTb4 - H - LE =0)
放射が黒球に注がれているときの黒球の温度上昇を知るために、
この式の解法として2通りがある。
その1:黒球温度の近似解法
その2:黒球温度の逐次近似法
その1では式の形が簡単になるので、黒球の温度上昇量がどのパラメータに
依存するかの見通しがつきやすくなり、観測データの整理方法の指針となる。
欠点は、観測値と計算値を比較したとき、僅かな違いは観測の誤差による
のか、計算の近似のせいなのか判断が難しくなることがある。
その2では、黒球温度が高精度で求まる代わりに計算時間が長くなるが、
上記の欠点は弱められる。ただし、計算を普通のパソコンで行う場合には
計算は瞬時に終るので、心配は無用である。
[その1] 近似解法:
計算式は次によって与えられる。
⊿T≡Tb-T=(R↓-σT4)/ {α+Cpρ(a/d)N }・・・・・(5)
ただし、α≡4σT13=4σ{T+(⊿T/2)}3
・・・・・・・・・・・・(6)
Tb は黒球温度、T は気温、T1 は T と Tb の中間温度、N は強制対流と
自然対流の両効果を含むヌッセル数[ 無次元:(a/d)N=ChU ]、a は空気の
分子温度拡散係数、 d は黒球の直径(m)、ChUは顕熱の交換速度(m/s)
である。詳細は「黒球の温度上昇の近似計算法」を参照のこと。
クリックして次の
「黒球の温度上昇の近似計算法」を参照し、プラウザの「戻る」を
押してもどってください。
式(5)右辺の分母を見てみよう。第1項の α は概略5W m-2K-1
程度の大きさ(水環境の気象学、表6.2)であり、第2項の Cpρ(a/d)N=
CpρChU も同程度である。従って、⊿T /(R↓-σT4)
は風速の逆数よりも緩い曲線で風速とともに小さくなることが分かる。
黒球の直径が大きく、入力放射量が大きければ⊿T が大きくなり、球の
まわりで発生する自然対流が卓越する。このときの N (ヌッセル数)
つまりChU (交換速度)が大きくなって⊿T が増大するのを抑制するように
作用する。
データ解析の指針:
データ解析では、縦軸に⊿T /(R↓-σT4)、横軸に
風速をとり、パラメータとして黒球の直径をとればよい。
[その2] 逐次近似解法:
当分の間、乾いた黒球を考えるので蒸発効率は β=0としておくが、
将来は半湿りの黒球を対象とする予定なので、式には β を含めておく。
ただし、この β には、水蒸気の分子拡散係数(D=2.54×10-5m
2s-1)と温度拡散係数( a =2.12×10-5
m2s-1)の比(D/a=1.2)の違いによる効果も
含む。
この効果を含めると、完全に湿った面に対してβ≒1.03程度になる
(Kondo,1967;Kondo, 1975)。
逐次近似法では、計算を繰り返して、次式を満たすような Tb を求める。
R↓-σTb4-H-LE=0・・・・・・・・(7)
H=CpρChU(Tb-T)・・・・・・・・・・・(8)
LE=LρChUβ(qSAT-q)・・・・・・・・(9)
ChU=(a/d)N・・・・・・・・・・・・・・・・・(10)
qSATは黒球温度に対する飽和比湿、q は周辺環境の比湿
である(計算プログラムでは水蒸気圧 VP を与える)。ヌッセル数 N は
黒球の直径 d を与えておけばプログラムの中で計算される。
詳細は「黒球温度の逐次近似計算プログラム」を参照のこと。
次の「黒球温度の逐次近似計算プログラム」
を参照し、プラウザの「戻る」を押してもどってください。
17.6 黒球温度の諸条件への依存性
逐次近似法で求めた計算結果を上述の「データ解析の指針」にしたがって
解析してみよう。
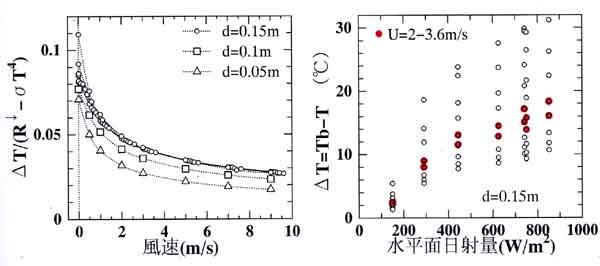
図17.1 (左)黒球の放射に対する温度上昇率(単位は
℃ W-1m2)と風速の関係、
黒球の直径=0.05m(三角、条件①のみ)、0.1m(四角、条件①のみ)、
0.15m(丸、条件①~⑦)の比較。
(右)直径=0.15mの黒球の温度上昇と水平面日射量の関係、赤丸は
風速が2~3.6m/s の場合。
(ⅰ)黒球温度の風速及び直径との関係
黒球の温度 Tb と気温 T の差 ⊿T を黒球の温度上昇とする。
この ⊿T は有効入力放射量(R↓-σT4)
と比例関係にあるので、温度上昇を有効入力放射量で割り算した値に
ついて風速との関係を調べると分かりやすい。
この割り算した量を放射に対する温度上昇率
と呼ぶことにしよう。
図17.1(左)は黒球の放射に対する温度上昇率
⊿T /(R↓-σT4)と風速との関係である。
黒球の直径 d=0.15m(丸印)については表17.1の
条件①~⑦の計算値、d=0.1m(四角印)と0.05m(三角印)については
条件①のみの計算値である。
諸条件について計算した、直径 d=0.15m(丸印)のプロットを見ると、
風速が1m/s 以上では、条件による違いはほとんど無視できることがわかる。
つまり、微風時は黒球の周りにできる自然対流が放射量の条件によって
異なるのに対し、風速>1m/s では黒球からの顕熱輸送量は強制対流による
効果が支配的になることを意味している。
次に生の黒球温度(Tb)と風速との関係を見てみよう。条件①と⑦の場合
について表17.2に比較して示した。
表17.2 黒球温度と風速の関係
①と⑦は、それぞれ夏の正午と年平均日平均の条件を想定(表17.1を参照)。
①夏の正午、気温=30℃ 条件⑦年平均、気温=15℃
風速(m/s) 黒球温度(℃) 黒球温度(℃)
d=0.15m d=0.05m 温度差 d=0.15m d=0.05m 温度差
0.3 58.51 51.99 6.52 19.29 18.06 1.23
1 52.43 45.64 6.79 18.09 17.06 1.03
2 48.35 42.25 6.10 17.45 16.58 0.87
4 44.53 39.35 5.18 16.90 16.19 0.71
10 40.24 36.36 3.88 16.31 15.80 0.51
表17.2を参照すると、黒球温度の直径による違いは4~6℃(日射の
強いとき)、ないし1℃(曇天を含む年平均日平均)程度であることがわかる。
(ⅱ)支柱からの熱損失などの影響
これまでの計算は、黒球を黒体と仮定し、その表面で放射と顕熱のみが
交換されるとして取り扱ってきた。市販されている黒球はつり金具や
支柱上に取り付けられており、それらを伝わって逃げる伝導熱もある。
こうした熱損失があれば、日中は、上で計算した黒球温度より低く観測
される。その差を解析すれば、実際の黒球に対する(伝導による
熱損失を含む)見かけ上のヌッセル数(あるいは交換速度)を知ることが
できる。見かけ上のヌッセル数は黒球ごと、また取り付け方法によって変わる。
この目的のための解析では、図17.1(左)の関係を作成すればよい。
実際の黒球は黒体でないので、その影響もある。そこで、黒球のアルベド
=0.05、赤外放射に対する黒体度=0.95とし、夏の正午の
条件①について、黒球の放射に対する温度上昇率を計算し、表17.3に
示した。
表17.3 黒球の放射に対する温度上昇率、
黒体とした場合とそうでない場合の比較
気温=30℃、黒球の直径=0.15m、夏の正午①を想定(表17.1を参照)。
(B)アルベド=0.05、黒体度=1.0
(C)アルベド=0.0、 黒体度=0.95
(D)アルベド=0.05、黒体度=0.95
風速(m/s) 黒 球 温 度 (℃) 温 度 上 昇 率(℃ W-1m2)
(黒体) (B) (C) (D) (黒体) (B) (C) (D)
0.3 58.51 57.41 59.02 57.90 0.0741 0.0745 0.0811 0.0817
1 52.43 51.51 52.72 51.78 0.0583 0.0584 0.0635 0.0638
2 48.35 47.59 48.52 47.75 0.0477 0.0477 0.0518 0.0519
4 44.53 43.92 44.61 43.99 0.0378 0.0378 0.0408 0.0410
10 40.24 39.80 40.25 39.81 0.0266 0.0266 0.0286 0.0287
条件(B)では日射の吸収が少なくなるので、黒球の温度は1℃程度低下する。(C)では
赤外放射の吸収が少なくなるが、黒球自体が出す赤外放射がより少なくなり
高温になる。(D)は(B)と(C)の中間となるが、日射量や大気放射量の
比率などによって変わる。
17.7 自然湿球温度(WBGT計算用)のあいまいさ
17.3節の問題点で指摘したように、WBGT(Wet-Bulb Globe temperature:
湿球黒球温度:単位は℃)の算定式(1)、(2)の右辺第1項に用いられる
自然湿球温度は、定義は簡単なようだが、
現実に観測される値は諸条件によって大きく変わる。
昔の気象観測で用いられていた非通風式の湿球温度計(棒状温度計、球部
の直径=9mm、フース型)にガーゼをまいた時の直径を10mm
(=0.01m)として検討する。同時に直径がその半分の場合も
計算する。
表17.1に示した夏の正午の条件①を想定する。この湿球に対する日射と風速
の当たり方によって湿球温度がどのように変化するかを計算し、結果を
表17.4にまとめた。
表17.4 自然湿球温度(単位:℃)の条件による違い
気温=30℃、水蒸気圧=25hPa、夏の正午①を想定(表17.1を参照)。
湿球の蒸発効率=1.03、黒体度=0.96、直径=0.01m及び0.005mとする。
(G)は風のみ自然の風速、赤外放射量=気温に対する黒体放射量とする。
(E)アルベド=0.3、球部が完全に空気中に暴露
(F)アルベド=0.3、直達光のみ遮蔽された状態
(G)アルベド=0.3、完全な遮蔽箱に入れた状態
(H)アルベド=0、球部が完全に空気中に暴露
(I)アルベド=0、直達光のみ遮蔽された状態
風速(m/s) 球部の直径=0.01m 球 部 の 直 径 = 0.005 m
(E) (F) (G) (E) (F) (G) (H) (I)
0.3 26.45 25.22 23.88 25.52 24.66 23.76 31.57 28.02
1 25.36 24.57 23.74 24.79 24.24 23.67 28.67 26.34
2 24.89 24.30 23.68 24.47 24.06 23.63 27.39 25.62
4 24.53 24.09 23.64 24.22 24.92 23.60 26.39 20.06
10 24.18 23.89 23.60 23.98 23.78 23.57 25.42 24.53
まず、計算結果の表17.4から、条件(E)~(G)を調べてみよう。
湿球温度計の球部に対して、風速の当たりが4m/s 以上の時の違い(誤差)
は1℃以下であるので重要にはならない。しかし1m/s 程度またはそれ以下
になるような設置方法では、誤差は2~3℃になることが分かる。
次に、直径=0.005cmの場合の条件(E)と(H)を比べる。
これは湿球のアルベドの影響である。アルベドの0と0.3による違いは、
微風時に4~5℃と大きい。風速4~10m/sでは、この違いは1~2℃程度
である。
また条件(E)と(I)の比較は、湿球温度計に対する日射の当たり方による
違いを示している。
実際には湿球のアルベドは材料や汚れなどによって 0.2 程度は変わると思わ
れる。また直達光や散乱光、地面反射光の当たり方(設置方法)によって、
湿球温度の違いは微風時には4℃程度、風が強く当たる場合には1℃
程度となる。
湿球温度における2~3℃、あるいは4~5℃の違いは、高温の許容基準
(17.2節参照)が1~2レベル、あるいは2~3レベル変わることに対応
する。
したがって、ここでは暑熱指数計などの器械による
温熱指標 WBGT の値を過信してはならない。はじめに述べたように、
器械よりも人体が感じる暑熱感覚が正しいことを忘れてはならない。
なお、条件(G)は通風式乾湿計の温度であり、風速1m/s 以上では
風速による違いは0.1℃程度で小さい。このことが
気象観測で通風乾湿計を用いる理由である。
以上の検討から、WBGT を評価する際に、日本の関係省庁で勧めている自然
湿球温度は、同一環境であっても現実的な器械で測られる値は変動幅(誤差)
が数℃もあるので、止めることを提案したい。
そのかわり、測定方法によってほとんど差が生じない通風式乾湿計による
湿球温度を用いる方法に改めよう。
通風式乾湿計ならば、湿球のアルベドとも無関係に湿球温度が決まる。
現実的には、この湿球温度は最近の湿度センサーで測った水蒸気量から
換算する。
この改善に際しては、高温の許容基準が少し変わってくることになる。
現状の WBGT を利用し器械だけに頼っていて事故が発生し、裁判で問題に
なる前に、 WBGT の曖昧さを小さくしようではないか。
要約
(1)熱環境の程度を表す指標である WBGT(湿球黒球温度)の算定式に用いる
自然湿球温度(放射のある自然状態に暴露して測った湿球温度)の曖昧さ
について理論的に検討した。
(2)現実的な測器による自然湿球温度には数℃のばらつきがあるので、
通風乾湿計を基準として、通風状態で測った湿球温度を用いて WBGT を算定
する方式に改めることを提案した。この方式だと、現在の高温の許容基準
は若干変わることになる。
(3)黒球の温度はその直径と風速によって変わることを具体的に示した。
(4)野外において研究的に行った黒球温度の観測データは、まず、放射に対する
温度上昇率と風速の関係について解析する(図17.1左)。理論式とのずれが
大きい場合は、黒球の実効的なヌッセル数(または交換速度)の違いとみる
べきだろう。また、小さなずれの原因として、黒球表面のアルベドや
黒体度の違いを考えよう。
(5)研究的な観測は、放射条件が簡単な平坦地で行おう。そこでは、直達光、
散乱光、地面反射光、大気放射量、地面放射量をきちんと観測(または計算
による推定)し、そのデータをもとに解析しよう。
図17.1(左)の関係が確かめられれば、放射条件が複雑な市街地に応用
(実用化)することができる。
参考文献
近藤純正、1982:大気境界層の科学、東京堂出版、pp.216.
近藤純正(編著)、1994:水環境の気象学、朝倉書店、pp.350.
近藤純正、2000:地表面に近い大気の科学、東京大学出版会、pp.324.
Kondo, J., 1967: Psychrometric constant for different sizes of
the wet-thermometer. Sci. Rep. Tohoku Univ., Ser. 5. Geophysics,
18, 125-137.
Kondo, J., 1975: Air-sea bulk transfer coefficients in diabatic conditions.
Bounary-Layer Meteorol., 9, 91-112.
Yaglou, C.P. and C.D. Minard, 1957: Control of heat casualtics at military
training centers. Am. Med. Ass. Archives of Industrial Health, 16,
302-316.
