"Time-dependent heterogeneity leads to transient suppression of the COVID-19 epidemic, not herd immunity",
Alexei V. Tkachenko et al., PNAS 2021 vol.118, No.17, e2015972118
https://doi.org/10.1073/pnas.2015972118
<序文>
・・・COVID-19(SARS-COV2)は感染症の疫学モデルに新たな展開をもたらしている。それは SARS-COV1 の時から注目されていた Superspreading つまり感染力の大きなバラツキや感染感受性や接触頻度の大きなバラツキが重要になってきたからである。均一感染モデル(従来の SIR や SEIR モデル)に比べて、感染規模(最終感染比率)FSE は小さくなり、集団免疫値(実効再生産数が 1以下になる免疫保持者比率)HIT が小さくなることは以前からよく知られていた。ここで注目すべきなのは、これらが考えるタイムスケールによって異なることである。Superspreading (overdispersion)の効果は感染力(infectivity)のバラツキを含んでおり、感染者が感染力を維持する5日程度の間でしか働かないから短期的な効果となるが、それにも寄与する長期的な因子、つまり感染されやすさ(susceptibility)や接触頻度(connectivity)は持続的な意味での効果がある。これらを区別することで、再発する感染波を説明できる。
・・・初期のアプローチでは、年齢層等の人口学的区分を追加してそれらの間の接触比率を見積もることによって、均一感染モデルを改良していたが、ここには感染感受性や空間的社会的構造に基づくネットワーク特性等は考慮されていない。
・・・スケールフリーネットワーク上でのモデルが開発され、数学的にエレガントな定式化がされて、例えば FSE は感染メカニズムの詳細には依存しないロバストな特性であることが示された。それは感染感受性の分布とその感染力との相関性のみに依存するのである。
・・・現実の感染症対策では FSE も重要ではあるが、日々の感染がどのように拡がるかについての研究が必要である。ネットワークモデルにおいて、数値計算も含めたアプローチで検討が行われて判った主なメカニズムは、「感受性や接触頻度の分布がある場合に、それらが大きなグループが優先的に感染して免疫保持者となるために、均一モデルに比べて感染の拡がりが早い段階で衰える」ということである。この傾向は感染感受性と感染力の間に相関がある場合には更に加速される。(ウイルスが増殖しやすい人はウイルスを沢山排出するという意味であるから、これは生理学的には妥当である。)このような解析は COVID-19 においても行われている[31,32,35 ,41,42]。
・・・以上の研究は感染の異方性(大きな分布)を固定的なものとして捉えており、短期的な異方性と長期的な異方性の区別をしていない。実際には、最初期の感染爆発の際には両方の異方性が寄与することで比較的早く感染が終息する(transient collective immunity TCI )ことが多いが、長期的な意味での HIT が達成されていない為に、対策を緩めると次の感染爆発が起きる。とりわけ今回の COVID-19 で顕著となったこのような状況に対応するために、この論文でのモデルが考案された。その特徴は本来確率論的に計算されるべきものでありながら、従来の SIR モデルや SEIR モデルの拡張として定式化されていることである。
・・・通例の均一モデルでは、実効再生産数 Re と基本再生産数 R0 とは感受性人口比率 S を介して、
Re = R0・S
という関係があるのだが、この論文のモデルにおいては、多くの場合、近似的に(多分長期的に)
Re = R0・S^λ
という関係がある。
HIT = 1 - S0 = 1 - R0^(-1/λ)
である。
この λ を免疫因子(immunity factor)と呼ぶ。
・・・免疫因子 λ には、生物学的(免疫応答、遺伝、年齢等)なものと、社会的(接触頻度等)があり、近似的にはこれらの積となる。アメリカでの感染事例を比較検討した結果、λ は過渡的(初期として) 4 ~ 5 位であり、長期的には 2 位である。
(例えば、R0 = 3 の場合、均一感染モデルでは HIT = 67%、λ=2,4,5 では、それぞれ 42%、24%、20% という事。)
・・・2020年6月末までの NYC と Chicago の感染状況を分析した結果、NYC ではかなり感染が拡がった為に、TCI が達成されていて、次の感染波は直ぐには起きないと予測されたのに対して、Chicago では感染があまり拡がらなかった為に、対策を解除すると直ぐに第2波が起きることが予測された。
以下、数式的な展開が続くが、後で追加することにする。とりあえずここまでで大体の事は判る。
<長期的な感染異方性だけの場合の定式化>
・・・ここではまず短期的な異方性を無視する。
感染感受性の因子を α として、<α> = 1 とする。またその分布を f(α) とする。
感染感受性因子 α を持つ人の感染性を Rα とする。
本来は個人毎にことなるのだが、単純化のために、同じ Rα を持つとする。
ネットワークモデルにおいては、α が結合数に比例するので、Rα ∝ α となっているが、
一般的にはそれほどの完全な比例関係とも言えないだろう。
・・・Sα を感染感受性因子 α を持つ人で未感染の人の(全人口に対する)比率とする。
jα(t) = -dSα(t)/dt = αSα(t)J(t) (1)
は、日々発生している感染者数である。J(t) は感染力(force of infection)と呼ぶ。
時刻 t より τ だけ前に発生した感染者は 時刻 t において、
RαK(τ)jα(t-τ) だけの二次感染者を生み出す。ここで、K(τ) は世代時間分布である。
従って、
J(t) = ∫ <RαK(τ)jα(t-τ)>dτ;積分は t まで (2)
と表せる。この2つの方程式は閉じていて、解くことができる。
Sα(t) = exp(-αZ(t));積分は t まで (3)
と形式的に積分すれば、
Z(t) = ∫<J(t')dt';積分は t まで
ということになる。また、全未感染者比率は、
S(t) = ∫f(α)exp(-αZ(t))dα = Mα(-Z(t)) (4)
実効再生産数は
Re(t) = (1/<α>)∫<αRαf(α)exp(-αZ(t))dα (5)
と書ける。
(以上、Rα が α に依存しない場合と α に比例する場合が、 Moreno et al. の susceptibility case と network case に対応している。)
以上の式を組み合わせると、
J(t) = ∫<K(τ)Re(t-τ)J(t-τ)dτ (6)
という発展方程式が得られる。
(1)式からは、
dS(t)/dt = -Se(t)J(t) (7)
と書くと、
Se(t) = <αSα> = -d(Mα(-Z(t))/dZ (8)
という形で、実効的な(感染力に対して応じる)未感染者比率の表現が得られる。
・・・Z(t) が小さい時、Sα(t) ≒ 1 - αZ(t) となることから、
Re ≒ R0(1 - (<α^2・Rα>/<α・Rα>)・Z(t)) (9)
係数部分を免疫因子 λ と名付ける。
λ = <α^2・Rα>/<α・Rα> (10)
α が生物学的な因子 αb と社会的な因子 αs の積であるように、
λ も生物学的な因子 λb と社会的な因子 λs の積である。
λb = <αb^2>/<αb>^2 = 1 + CVb^2 (11)
λs = <αs^3>/<αs><αs^2> = 1 + CVs^2・(2+γsCVs)/(1+CVs^2) (12)
CV は分散係数、γは skewness である。
2つのケースの中間を表現するために、パラメータ χ を導入する。
つまり、
Rα ∝ α^χ
とすると、χ=0 と 1 が生物学的な因子と社会学的な因子を表す。
COVID-19 の場合は、感染性の観察から、殆どが社会的な因子であると思われる。
・・・一般的な非線形領域においては、f(α) がガンマ分布であるときに単純な表現が得られる。
f(α) ∝ α~(1/(η-1))・exp(-α/η)
Se(S) = S^(1+η) (13)
Re(S) = R0・S^λ (14)
λ = 1 + (1+χ)η
HIT は
1 - S0 = 1 - (1/R0)^(1/λ) (15)
Figure.1 に(13)式が図示されている。感染の進行によって未感染者比率 S が下がり、それに比例して実効再生産数が下がるというのが、均一感染モデル(破線)であるが、感染性に分布がある時(λ>0)は、感染性の高い人々が先に感染するためにもっと急激に下がる。
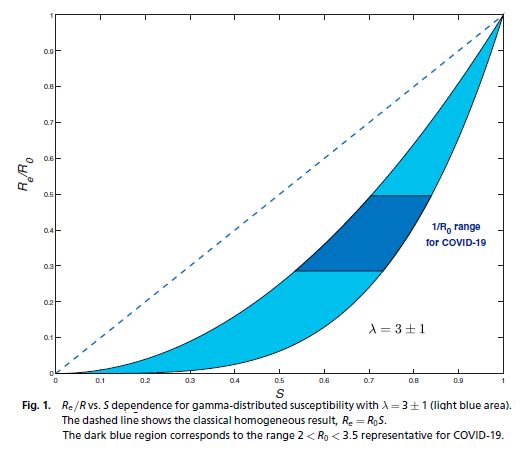
Appendix ではガンマ分布ではなく、ベキ状分布や対数正規分布の場合の結果が述べられているらしい。
<社会的活動の短期的な変動の役割>
・・・感染頻度の短期的な過剰分散は全体としての疫学動態に影響を与えないとされている。これは個人毎の感染感受性との相関が無いからである。しかし、感染頻度の自己相関(持続時間)が世代時間の程度まである場合には、影響を与える。この短期的な影響は持続的な感染感受性の分散に加えて短期的な分散項が加わる形に表せる。詳細は Appendix を見ないと判らない。
・・・社会的活動についての様々な研究[45,46,47,13,37,48,19]から、f(α) が exp(-α/<α>) (ただしカットオフがある)で表されることが判っているらしい。これから λ=3 となるのであるが、長期的な値 λ∞ は 2 位であると推定される。これもモデル計算[18] と一致するらしい。
<COVID-19 の実例への応用>
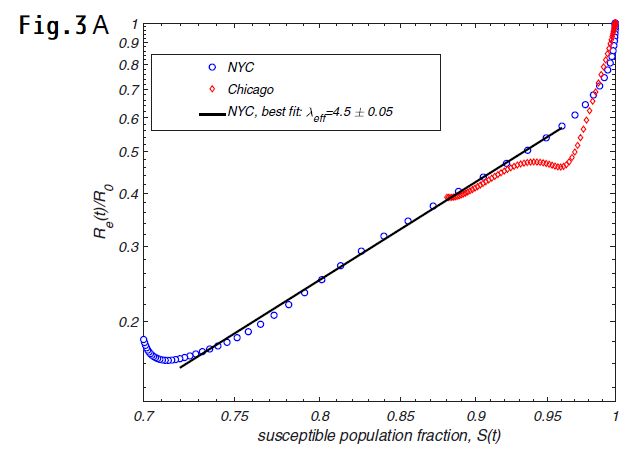
・・・2020年3月に起こったアメリカ各都市での感染爆発の解析がいろいろなモデルで行われていて、それをまとめると λ=4~5 位である。これは短期的な感受性分散の効果と思われる。解析方法は著者の一人 Wong 氏の[43]を見ないと判らない。Fig.2 に 1-S と R0 のプロットがある。
・・・Fig.3 A にはNYC と Chicago での Re(t)/R0 と S(t) の関係がプロットしてある。よく判らないのは、Re に対しては政府の行動抑制の効果が相当入っている筈なのに、そのまま議論してよいのだろうか?ということである。いずれの都市も初期に急激に Re が低下し、その後、指数関数的な変化をしている。この初期の急激な減少がロックダウンの効果とすると、安定した部分というのが、集団免疫効果なのだろうが、これはほぼ λ= 4.5 で説明できる。つまり、ロックダウン最中の感染拡大においてはロックダウン効果そのものが一定と考えるのだろうか。それにしても、NYC での S(t) は 0.75 に達している。25% もの人口が感染したのだろうか?これに対して、Chicago では 10% 程度と読み取れる。
実際のデータを調べてみたら(https://www.jmedical.com/home/stopcovid19/covid-nyc-data/, https://github.com/thecityny/covid-19-nyc-data/find/master . )2020/5/13で NYC陽性者累積185,000人位である。NYCの人口は8,500,000位であるから、2.2% ということになる。一桁違う。シカゴについては、60,000人位(ただし終息していない)で人口が2010,000人だから、3%程度である。(https://www.chicago.gov/content/dam/city/sites/covid/reports/CDPH-COVID-Reopening-metrics_070221.pdf )
<TCI の脆弱性>
・・・Fig.3 A は感染第1波である。NYC ではかなり感染が進んでしまい、Chicago では途中で止まった。この段階では最終的な HIT には達していない。 TCI である。その後対策を緩めると再感染が起きる。これをいろいろな λ を想定して計算している。
・・・どうも参考文献や Appendix を読まないとよく判らないので、この論文はとりあえずここまでとする。日本とは感染爆発のレベルが桁違いのようであるので、どこまで参考になるかについてはやや疑問である。
・・・この論文には更に続きがあって、SIR 乃至は SEIR モデルの形式に嵌め込んだ定式化まで行っている。相当ややこしそうである。
"Stochastic social behavior coupled to COVID-19 dynamics leads to waves, plateaus and an endemic state",
Alexei V. Tkachenko et al., https://doi.org/10.1101/2021.01.28.21250701
・・・これは想像であるが、感染感受性は長期的に見た平均値の周りを揺らいでいて、その揺らぎの持続時間が問題となる。この持続時間を過ぎてしまえば、再生産数に与える影響は平均値としての感染感受性で決まるのであるが、持続時間内であれば、短期的な感染感受性で決まる、ということなのだろう。この感受性にはその人毎の他人との接触頻度の因子が含まれているから、確かにそういうことはあり得る。接触頻度の高い人が感染して社会活動が維持できなくなると、それまで接触頻度の低かった人の活動度が上がることになる。いずれにしても、著者がこのような発想をするに至ったのは、いろいろなデータから推定された λ=2 という感染感受性のバラツキパラメータが、実際の感染爆発で推定されたパラメータ λ=4~5 と合わなかったからではないか、と思われる。したがって、理解するためにはそのパラメータ推定の中身にまで立ち入らなくてはならない。これは結構労力を要するだろう。
(追加:2021.12.10)上記論文の内容
・・・個人の活動度 αi が下記のような揺らぎを持つとしている。
dαi/dt = (<αi>-αi)/τs + ηi(t)
<ηi(t)ηi(t')> = (2αi(t)/(τs・k0))δ(t-t')
τs は揺らぎの緩和時間で 30日としている。第1項は平均値へと終息する傾向を表現している。
揺らぎの分散は <αi>/k0である。k0 は揺らぎの強度パラメータ(小さいほど揺らぎが大きい)。
<αi> は個人としての活動度の平均値であるが、社会全体としてはその個人平均値がガンマ分布に従うと仮定している。
その分散パラメータが κ である。
κ=1 は指数関数的分布に相当する。
ここでは、そこまでの過分散は避けて、κ=2 としている。
短期的な分散は 1/k = 1/κ + 1/k0 ≒ 3 という事が知られているので、k0=0.4 とする。
(ガンマ分布は、 f(x)=(λ^κ/Γ(κ))x^(κ-1)exp(-λx))
感受性人口比率は平均活動度=<α>によって分類され、さらに、それが時間的に変動する活動度 α にも依存する。それについての微分方程式は、感染を受けることによる減少項と活動度が変化することによる拡散項と回復項との和になる。
dS<α>(α,t)/dt = {-αJ(t) + (α/k0τs)∂^2/∂t^2 + ((<α>-α)/τs)∂/∂t}S<α>(α,t)
ここで、
S<α>(α,t) = exp(-Z(t)<α>-k0h(t)α)
として、Z(t) 持続的、h(t) 一時的、と感染性のバラツキを対応させる。
更に、感染者数の活動度重み平均 I(t) = <Ii・ai(t)>i/<ai^2>i: Ii は感染状態で 1 非感染状態で 0 を定義する。
感染力 J(t) は
J(t) = γR0M(t)I(t)
となる。ここで、M(t) は社会的感染抑止策の因子である。
これら3つの量についての微分方程式が成り立つ。
dI(t)/dt = J(t)S(t)^λ/(1+h(t))^2 - γI(t)
dS(t)/dt = - J(t)S(t)^(1+1/κ)/(1+h(t))
dh(t)/dt = J(t)/k0 - h(t)(1+h(t))/τs
パラメーターは、
世代時間(の逆数):γ=0.2
感受性揺らぎ(の逆数):k0=0.4、
感受性の定常分布のバラツキ(の逆数):κ=2、
感受性揺らぎの相関時間:τs=30、
感受性の定常分布に由来するimmunity因子:λ=1.7
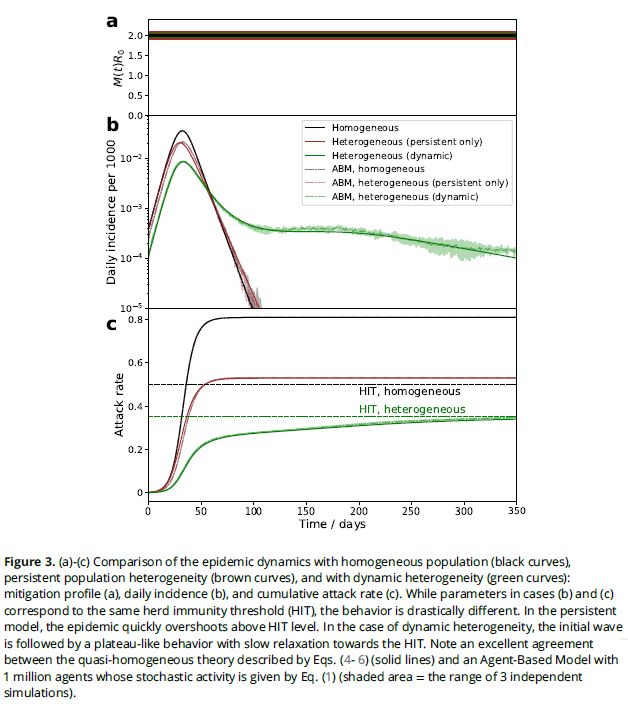
・・・Figure 3 に計算例がある。M(t)=1 としているようである。R0 は 2.0 としているようである。黒線は均一系の SIR モデル、茶色が感受性分布が一定で揺らぎのない場合、緑色が感受性分布に揺らぎがある場合。ABMというのはここでの計算ではなく、このモデルに基づく確率的シミュレーションの結果である。黒線を見ると、M(t)R0=2 でありながら、50日位で感染が自然終息してしまっているから、この計算というのは初期値が相当大きいと思われる。SIRモデルで試しに計算してみると、新規感染者数の最大が32日目位になるように初期値を決めると初期 attack rate(発病者数=積算感染者数)比率=0.0005 位であることが判る。東京都で言えば7000人で、これは去年の夏頃までの積算陽性者数である。つまり、日本の状況ではこれらのモデルによる感染プロファイルの違いが生じる前に、行動制限による感染の終息が起きている。ニューヨーク市で言えば4200人だから、去年の3月末の段階に相当するので、確かにニューヨーク市での感染第1波の始まりに相当する。
・・・感染が収束していく段階において、だらだらと長引く(プラトーが生じる)というのが感受性の揺らぎの効果として出てくるようである。感受性が小さくて感染を免れた人が揺らぎによって感受性の高い状態になって感染する、という事があちこちで起きるためと考えられる。その状態が長く続いている間に感染対策が緩んでしまうと(M(t)が上がってしまうと)次の感染爆発が起きる、という事であろう。そういう意味では日本においても同様な事になっている。第5波が収束したように見えて、あちこちで時々クラスターが発生している、という現状に相当するのかもしれない。