・・・ネットワークを作り方で説明してある。m0 個の独立 node を作る。1ステップ毎に 1つづつ頂点(vertex)が追加されて、そこから既存の node に対して m 個の結合が作られるのだが、その確率は ki/∑kj とする。(一番最初は ki=0 なのだが、まあ 確率 1 とするのであろう。)これを多数回繰り返すと P(k)∝k^-3 となるらしい。<k>= 2mとなるらしい。ここではm0=5、m=3 としてある。
P(k)= 2m^2/k^3 となる。m は最小の kである。<k^2>∝log(N)となって、人口サイズと共に対数発散するから感染閾値を持たない。但し、最終感染比率R(∞)~exp(-1/λm)となる。これは以下の数値計算(N=10^6、λ= 0.09)で確認されている。
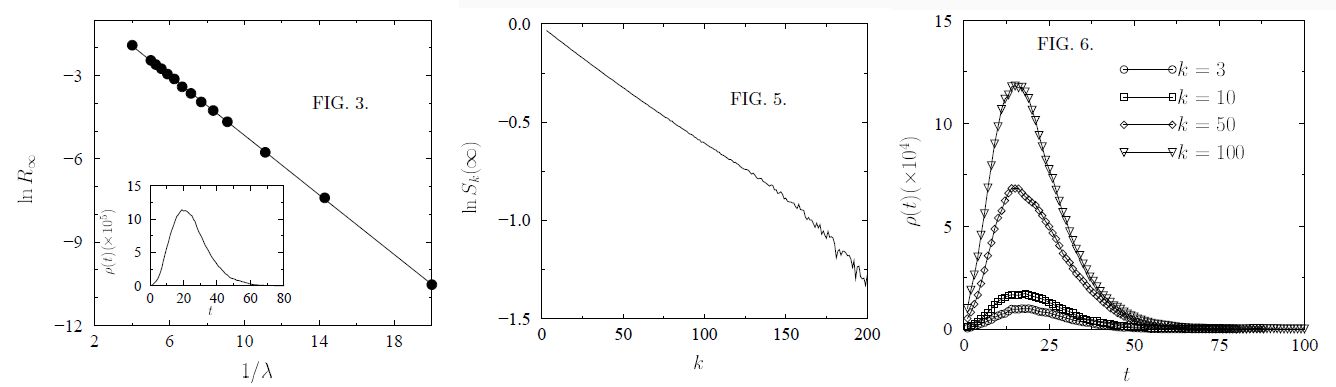
・・・Fig.3 には N=10^6 での 1/λ に対する R(∞) の計算結果が示されている。また λ=0.9 についての感染者比率 ρ(t) の時間変化も図示されている。ρ(t) を積算すると R(t) になるわけだから、目分量で R(∞)=0.005 位だろう。ln(0.005)=-5.3 位なので、メインのグラフから見ると λ=0.09 の間違いだろうと思う。
・・・Fig.4 は意味が判らない。シミュレーションでは、10^4 から 10^5 回の感染爆発を確率的に計算して、最終感染比率の平均値を採用して、Fig.3 にプロットしているらしい。積算確率 P(R∞>R) というのは、どういう意味だろうか?そもそも横軸の R が回復者比率とすれば、1 より大きい筈がない。
・・・Fig.5 は Sk の k 依存性が exp(-λkφ) となることの実証である。
・・・Fig.6 は書いてある通り、驚くべき結果である。初期条件としては、これまでは各 k に均一に感染者比率を与えていた(ρk(0)=ρ0) のだが、特定の k だけに初期感染者を入れると、感染のサイズが大きく変わるが、感染の時間経過は変わらないのである。
・・普通の SIR モデルと比べてみよう。大きな k の初期感染者は k に比例した感染力を持つから、普通の SIR モデルでは、初期感染者数が k 倍あるという状況に相当する。だから、その場合には感染初期には感染者数が k 倍になる。しかし、その分だけ集団免疫に達する時間も早くなるので、総感染者数は変わらない。つまり、人数軸方向で k 倍になる代わりに 時間軸方向で 1/k になる。しかし、スケールフリーネットワークにおいては、人数軸方向だけが k 倍になって時間軸方向は変わらないのである。これは集団免疫のメカニズムが異なることを意味している。
・・均一初期条件の Fig.4 の場合を Fig.5 に書き加えるとすれば、k=3 の場合よりも下に来る感じである。これはよく判らない。k について均一分布なのだから間に来るのが自然ではないだろうか?
・・現実の接触者数分布がこれに近いとして、感染プロファイルを比較する為には、ここでの λ や m 等を見積もらねばならない。しかし、そもそも このモデルでは R0 が 0 に近いのであるから、λ を推定することが出来ない。感染プロファイルの初期を比較して見るしかないだろうが、実際の新規感染者数の推移はここでの ρ(t) には対応していないことにも注意すべきである。簡単な比較として、例えば感染の波の継続時間から推定できるかもしれない。今までの5つの波は高さが違ってはいても継続時間は同じくらいであるから、ある程度このネットワークモデルの状況に近いと言えるのかもしれない。解釈としては、感染力の高いウイルスが感染の波を引き起こす場合、接触数の大きな人口グループの間に早く感染が拡がるために、感染者数は急速に増加するが、平均としての接触数は減少していくために、予想よりは感染が早く終息してしまう、ということである。こういう状況を数値計算で例示出来れば面白いだろう。