2020.09.23
      ９月９日に読んだ台湾の Chengさんの論文に引用されていた、確率モデルの論文を読んだ。
Joel Hellewell et al.,
"Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts",
Lancet Glob Health. 2020;8(4):e488-e496. doi:10.1016/S2214-109X(20)30074-7
４月号に掲載されているが、２月頃書いた論文であるから、まだパラメータが最新ではないが、なかなか優れた論文だと思う。
疫学モデルには SIRモデルとその近縁種のような『決定論的 deterministic』なモデル、つまり、感染者数についての微分方程式あるいは遅延微分方程式によって記述されるモデルと、『確率的 stochastic』モデル、つまりあらかじめ設定された確率に従って個人の事象毎に乱数を発生させて決めるモデルがある。分子計算における、平均場近似と計算機シミュレーションの違いみたいなものである。確率的モデルは複雑な構造のモデルを計算できるが、多数の試行を行ってその平均や分布を議論するため、因果関係が判りにくくなる、という欠点もある。また、実測の感染者数推移を再現するというようなことができない。こういうモデルは初にお目にかかったので、少し丁寧に読んだ。

      モデルの仮定は事象の確率分布の設定である。ここでは以下の設定をしている。計算の全体の流れは図１を見ると判りやすい。

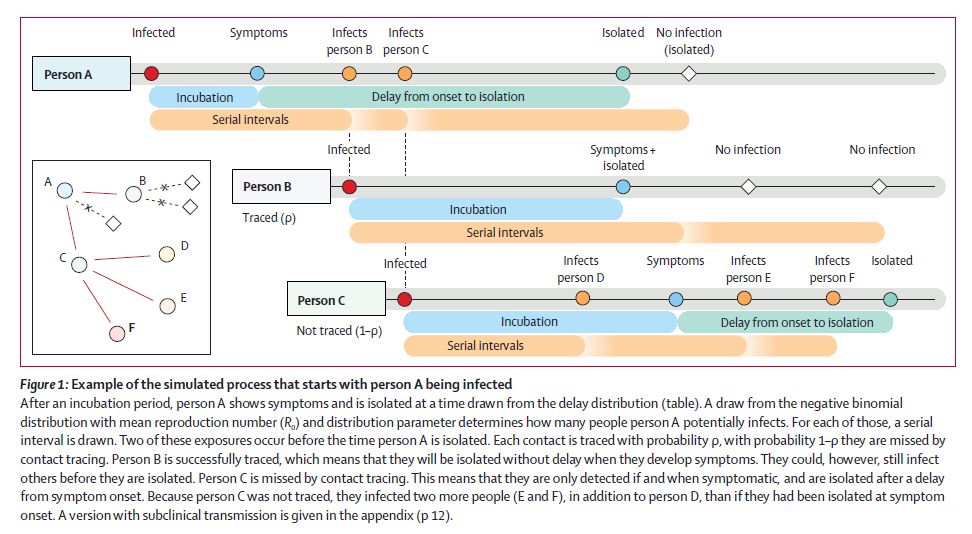
１．基本再生産数R0を1.5, 2.5, 3.5のいずれかに設定する。もっとも、これは３月頃の推定値である。
      これによって、1人の感染者が放置すれば平均として何人に感染させるかが決まるが、その時間的分布や個人差は決まらないので、確率分布を与える。その個人差の分布関数にはどうやら研究の歴史があるようで、負の二項分布が使われている。その分布の平均値が R0 である。乱数を発生させてこの分布に従って R0 を決めれば、その感染者が何人に感染させる予定であるかが決まる。以下このやり方の繰り返しなので、判りやすく説明しておくと、例えば分布関数を φ(x) として、x が 0〜1 の範囲だとしよう。また、φ は規格化して（最大値で割って）最大値が 1 になるようにする。0〜1 の一様乱数 x と y を出し、φ(x)≦y であれば、その値 x を採用する。そうでなければ、再度試行し直す。こうすれば、φ(x) の確率で x が選択できる。
  （決定論的なモデルとの比較で注目すべきは、感染率 β とか、治癒率 γ が登場せず、単に、基本再生産数 R0＝β/γ だけが登場することである。γ に相当する量は、下記の設定 3 における SID の分布の拡がりである。）

２．感染のタイミングは serial interval distribution（SID）に従って確率的に決める。
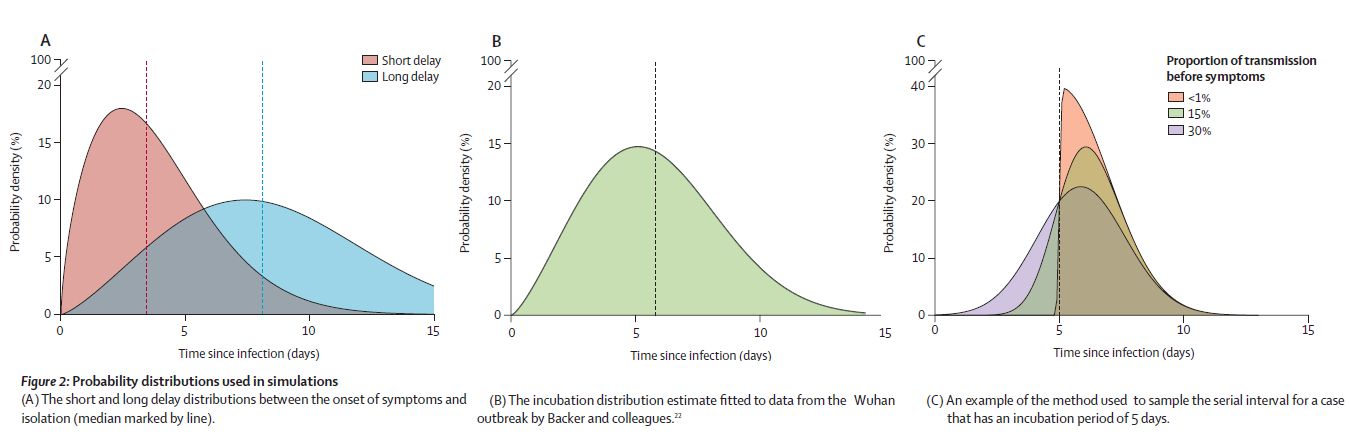
      SID は一次感染者と二次感染者の発症日間隔の分布であるが、ここでは感染日間隔の分布と考えている。分布としては同じものである。この分布は、本来は実測による推定分布が使われるべきなのだろうが、まだ知られていなかったのだろうか？ここでは、実測による潜伏期間分布（図２b）と次の仮定から決めている。

３．発症前に感染させる比率を ＜1%、15%、30% と設定する。（現在では約40%という比率でコンセンサスが出来ている。）
      この設定を使い、SID を逆に決めている。ただし、SID は 歪正規分布とする。
      SID(x,λ)＝2f(x)F(λx)、λ＞0
      φ は正規分布であり、F は f を−∞から λx まで積分したものである。具体的には、図２c である。
  まず、潜伏期間を乱数を使って決める（例として 5日）。それを平均値として分散が２日となる正規分布 f  を決める。（この２日という分散の根拠は示されていないが、これが感染能力持続時間を決めているので、γ に関係する。 γ＝1/4 程度と考えられる。結果的には実態に近い。）
  これに、上記の歪因子 F を掛けることで分布の左側を小さくして、潜伏期間よりも短い部分の比率を ＜1%、15%、30% に合わせる。
  SIDを決めることで、２．で決められた各感染のタイミングを乱数を使って決めることができる。

４．こうして、一次感染が起きた時刻から見て、二次感染が起きる時刻が決まるのだが、一次感染者が隔離されれば、二次感染は起きない。
  そこで、発症から隔離までの経過時間の分布を仮定する。これは、SARS の場合と 武漢での初期での場合の２通りの実測分布を使う。
  それぞれ、Short Delay（平均3.43日）, Long Delay（平均8.09日） であり、図２a に示してある。
  （日本の場合は ５〜６〜７日。都市によって異なる。）

５．発症して隔離されるタイミングでその感染者に対する聞き取りを行い、接触追跡（contact trace）が行われる。
  それがどれくらい成功するかという確率を、0,20,40,60,80,100% で仮定する。つまり、隔離されたタイミングにおいて、その感染者がそれまでに接触した人物がこの比率で同定され、その同定された人物については「発症した時点において」隔離される。（発症前の感染については防止できない、という仮定である。なぜ同定した時点でないのか、PCR検査をすればよいのに、というのはやや疑問が残るが。。。）

６．不顕性感染者（subclinical infection）の比率は 0%、10% を設定する。症状を出さない感染者は隔離されない、という仮定である。この扱いは Appendix で記述されるとあるが、Appendix は無いので、判らない。発症しないので、２次感染のタイミングをどうやって決めるのかが問題だろう。しかし、感染させる人数は決まるはずなので、あまり問題ではないかもしれない。

以上の確率分布や確定確率の設定条件において、初期感染者数として、5,20,40名の感染者を置き、乱数を発生させて、1000回のシミュレーションを行った。
12〜14週目において、新規感染者が無い、というのが終息条件だが、その途中で、累積感染者が 5000人を超えた時点で GiveUp するのである。
こういった条件の根拠については何も述べていないが、国や地域で変わるだろう。初期感染者数が変わっても、それに比例した結果しか出ないと思うのだが、
初期感染者数依存性は、平均的なモデル（決定論的なモデル）では単なる比例計算に過ぎないが、個人的な感染性のバラつきの効果は平均的なモデルでは捉えられないようである。多くの感染は superspreader と呼ばれる少数の感染者によって起こることから、初期感染者数が少なくなると、比例計算以上に感染拡大の可能性が下がることが知られている。Overdispersion 効果というらしい。その仕組みは下記を読むと判るらしい。。。
J. O. Lloyd-Smith et al., Superspreading and the effect of individual variation on disease emergence, Nature, Vol 438|17 November 2005|doi:10.1038/nature04153
勿論、これだけだと、努力すればそれだけ良いという話になるので、その代償として、必要になった１週間での接触追跡の数を評価して実現性の議論につなげようとしている。

図３A が標準的な条件：
初期感染者20人、隔離遅延が短い、発症前感染が15%、不顕性感染 0% の場合における、R0＝1.5,2.5,3.5 での、感染終息した場合の割合を示す。
（この頃はまだ発症前感染の可能性が示唆されていただけであった。）
図３B は実効再生産数で、大体 Reff＝1 の辺りが、終息割合 50% 位に対応しているようである。
Contact Tracing＝0 の処が、R0 よりも少し下がっているのが、隔離効果である。Contact Tracing を真面目にやれば、より大きな効果が得られる。
（ これが日本において初期感染抑制の為に使われた手法であるが、残念ながら、それだけでは Reff ＜ 1 が達成できなかった。）

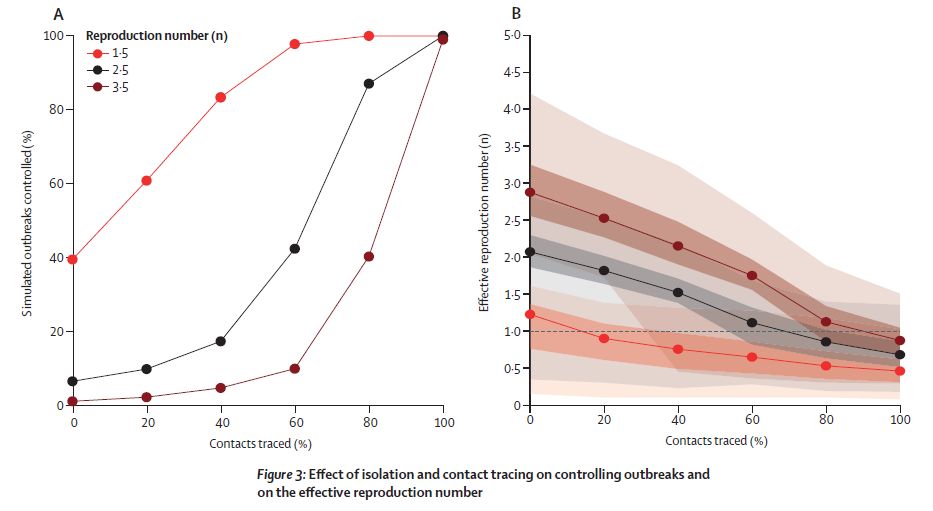
図４A は R0＝2.5 で、初期感染者数を変えた場合である。Overdispersion 効果が見られる。（ 少数だと、たまたまその中に superspreader が居た時だけ感染爆発が起きるという意味なのだろう。）
図４B は 隔離遅延の効果である。遅れると感染爆発が抑えられない。
図４C は 発症前感染の割合の効果である。これが大きいと感染爆発が抑えられない。
図４D は 不顕性感染者比率の効果である。これが大きいと感染爆発が抑えられない。

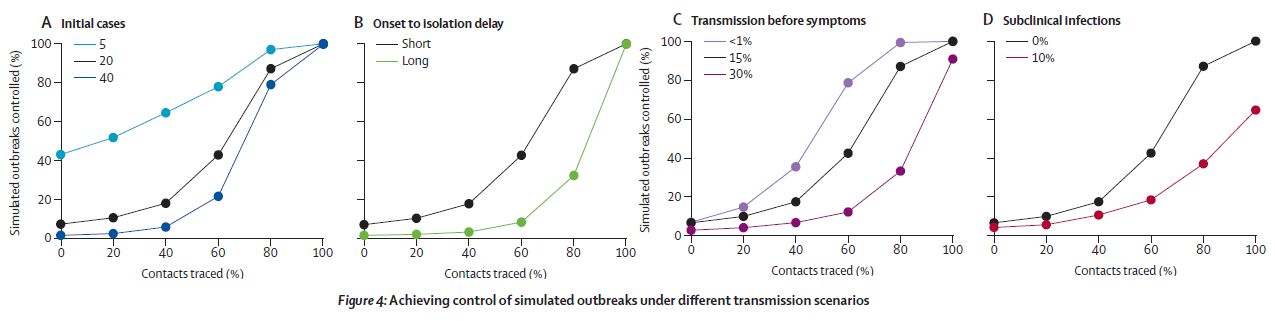
図５には、隔離遅延が短い場合と長い場合について、それぞれ R0＝1.5,2.5,3.5で、必要となる毎週の Contact Tracing の手間を表す。
この確率モデルの中で、決定論的モデルで実現できないのは、Overdispersion 効果と、contact tracing の効果だろう。他は、同じような計算が可能である。