誘導場の計算方法

誘導場の計算方法　深水らの側抑制モデル

●　深水らの側抑制モデル

　深水，吉田らは，横瀬の４つの場の基本公式を使って様々な図形の場の数値シミュレーションを試みた¹⁾．その結果，基本的に場の数値シミュレーションは，横瀬の実験結果と良く一致することを示した．ただし，誘導場の計算はすべて積分演算であることから，線分を太くする，線分先端の計算精度をあげるなど，誤差の累積を防ぐための修正が必要である．
　一方，深水，吉田らは，誘導場の詳細な再現実験を行ったところ，横瀬の報告にはない図形の近傍の分布が見い出された49)．この分布は，横瀬の４つの場の基本公式の数値シミュレーションに修正を加えても対応できなかった¹⁾．
　そこで，深水，吉田らは横瀬の基本公式の理論的見直しを行った²⁾．まず，磁場では場の吸い込みがあるため心理実験結果と矛盾しており，誘導場は静電場ポテンシャルの解釈に近いことを指摘した．しかし，Laplace の方程式による静電場ポテンシャルφ を計算したところ心理実験結果を再現できなかった．このため，電荷分布が座標(x, y) に依存する等質でない電荷ρ (x, y) と仮定し，Poisson の方程式でポテンシャルφ を計算した結果，図形近傍における場の分布の尻切れ状態のみを再現できた． Laplace ，Poisson 方程式は次の通り。

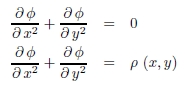
　以上のように，純粋な静電場モデルでは場の吸い込みはないが，実験結果を充分再現することは困難である．また，Poisson の方程式のρ (x, y) のような電荷分布が等質でないという仮定は，個々の図形ごとに決めなければならず，汎用の誘導場の基本公式として利用するには問題がある．
　このような静電場モデルの問題点に鑑み，深水，吉田らは自らが測定した誘導場の分布を説明できる新たな計算モデルを提案している．まず，藤井の側抑制モデル³⁾を利用した計算モデルの検討を行った⁴⁾．すなわち，網膜上の任意の点の出力 o(x, y) は，刺激図形 i (ζ, η) と結合係数 w (x, y) の畳込み積分で表される³⁾．

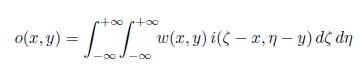
深水，吉田らは，この式が図形の場を再現できるように結合係数 w (x, y) を心理実験値から求めた．

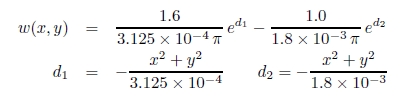
　これら，畳込み積分と結合係数による側抑制モデル F(0) は，Laplace ，Poisson 方程式による静電場のモデルよりも心理実験結果を再現できることが示されている⁴⁾．

　そこで，側抑制モデル F(0) を基本に，視空間の異方性，空間周波数特性，網膜神経密度，図形濃度，更に実験条件の補正を加えて，更に心理実験の再現性を図った計算モデル F(1) を提案した^{5), 6)}．
　まず，刺激図形 i (ζ, η) の図形濃度を次のように定義する．

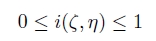
ここで，白の地は i = 0，無反射の黒領域は i = 1である．このとき，側抑制の出力 o(x, y) を用いて，図形近傍の小光点の閾値 Sr (x, y) を次のように表す．

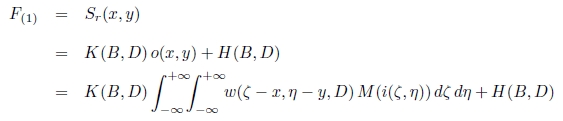
ただし，D は視距離，B は環境照度，K(B,D) は側抑制の出力から閾値へのスケーリング変数，H(B,D) は閾値の飽和，M(c) は刺激強度 c に対する受容強度である．
側抑制の結合係数 w (x, y,D) は，

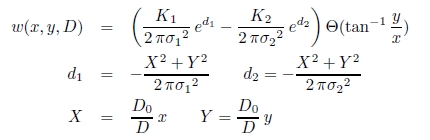
で表される．ただし，σ₁₍₂₎ は興奮（抑制）部の空間定数，K₁₍₂₎ は興奮（抑制）部の応答，X, Y は基準視距離に変換後の空間スケーリング値，D₀ は基準視距離(2000mm)，Θ は方位別強度関数である． F(1) モデルに，実験的に求めた受容強度 M(c)，結合係数 w(x, y,D)，方位別強度関数 Θ，更に K(B,D)，H(B,D) を用いて，シミュレーションを行った．
　その結果，F(1) モデルは心理実験結果との整合性が著しく高い（誤差5%以内）ことが示された^{5), 6)}．F(1) モデルは，F(0) モデルのように図形によって結合係数が異なることがないため，一般性が非常に高い．今後，濃淡や色のある図形などの場のモデルの拡張と図形視などの理論的解析が期待される．

●　ニュ－ラルネットによる計算モデル

　中島らは，ニューロンの受容野関数を，藤井らの側抑制モデル³⁾のような，ガウス関数の線型結合で表されるDOG(Difference Of two Gausian) 関数ではなく，視覚の誘導場の効果を入れた新しい関数に置き換えた誘導場の計算モデルを検討している⁷⁾．

　横瀬の誘導場の基本式を離散化した空間で表現すると，点 P₀ におけるポテンシャル P(P₀) は次式で与えられる．

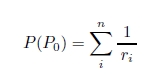
ここで，r_i は点 P₀ と線分 ab を構成する n 個の任意の点 P_i の距離である．この式から，ポテンシャルは各構成点からの距離 r_i の逆数の和である．そこで，r_i の逆数をニュ－ロンの結合荷重とした心理的ポテンシャル生成ニュ－ラルネット(Potential created Neural Network; PCNN) を考える．そして，次のような距離の逆数関数を，PCNN の新しい受容野感度関数DIP (Difference of two Inverse Proportion) とする．

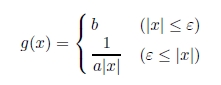
ただし，ε = 1/ab，a は画像のぼかし具合を調節するパラメータ，b はニュ－ロンの興奮の飽和を規定するパラメータである．
　中島らは，誘導場の分布を直接求めるモデルは提案していない．しかし，上の式 g (x) によるニュ－ラルネットの入出力関係を空間周波数領域，具体的には，この式をフーリエ変換し，その周波数特性を調べている．上式 g (x) のフーリエ変換 G (ω) は，

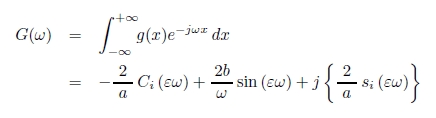
で表される．ここで，C_i，s_i はそれぞれ，

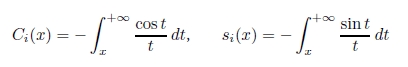
である．これらの式を用いて，シミュレーションした結果，PCNN は，図形の体制化，ポッゲンドルフ錯視など，幾何学的角度方向錯視現象の錯視量の定量的な説明に有効なことが報告されている⁷⁾．

●　側抑制モデルの今後の展開

　工藤らは，誘導場と図形の輪郭線の太さ，色，濃度の関係を明らかにする測定において，小光点を徐々に明るくする，または暗くする場合によって，誘導場の分布が異なる実験結果を説明するモデルとして，側抑制モデルを検討している⁸⁾。
　前述のように，深水らの側抑制モデルをベースにした誘導場のモデルは，心理実験結果との整合性が非常に高い。そして，色，濃度のある図形の誘導場を解明中の工藤らの研究でも，側抑制モデルの有効性が着目されている。
　今後，これらの研究が進み，色，濃度のある図形の誘導場の側抑制モデルによる精密なモデルの構築が期待される。

参考文献

1) 深水義之, 吉田登美男, 小谷津孝明, 野田健一, 諸角建. 横瀬「場の理論」のコンピュータシミュレーション　―景観の図形認識の立場からの解明と評価に関する研究(1). デザイン学研究, Vol. 92, pp.43-50, 1992.

2) 深水義之, 吉田登美男, 伊藤明, 小谷津孝明. 電磁気学による横瀬の場の理論的見直し　－景観の図形認識の立場からの解明と評価に関する研究(3) －. デザイン学研究, Vol. 42, No. 6, pp.39-46, 1996.

3) 藤井克彦, 松岡章, 森田龍彌. Lateral inhibition による錯視図形の解析. 医用電子と生体工学, Vol. 5, No. 2, pp.117-126, 1967.

4) 深水義之, 伊藤明, 吉田登美男, 白石照美, 小谷津孝明. 側抑制に基づく図形の解析　－景観の図形認識の立場からの解明と評価に関する研究(4) －. デザイン学研究, Vol. 43, No. 2, pp.69-76, 1996.

5) 深水義之, 伊藤明, 吉田登美男, 白石照美. 心理実験に基づく視空間伝達モデルの提案　－景観の図形認識の立場からの解明と評価に関する研究(6) －. デザイン学研究, Vol. 45, No. 4, pp.75-82, 1998.

6) 吉田登美男, 深水義之, 白石照美, 伊藤明, 小谷津孝明. 心理ポテンシャルの心理物理的伝達関数の誘導と錯視への応用. ラウンドテーブルNo.28, 日本心理学会第62 回大会, pp. 23-32, 1998.

7) 中島和樹, 菅沼義昇, 伊藤正美. 心理的ポテンシャル場とニュ－ラルネットによる図形認識. 電子情報通信学会技報, Vol. PRU90-155, pp.79-86, 1990.

8) 工藤博章，安藤理恵，大西昇:"視覚の誘導場を形成する上下弁別閾に対する側抑制モデルによる検討", 電子情報通信学会総合大会講演論文集 2007年基礎・境界, AS-10-1, pp.S-109-110, 2007

本ページの原典
長石道博: "視覚の誘導場によるパターン認知の研究", 豊橋技術科学大学博士論文乙第142号 (2000) 　[学位論文]