誘導場の計算方法

デジタル画像における誘導場の計算モデル

●　デジタル画像における計算モデル

　横瀬の４つの場の基本公式は，直線と円で構成された図形の誘導場計算しかできない問題がある．一方，深水，吉田らや中島らの生体工学的な計算モデルは，デジタル画像のような離散的な画像の誘導場を計算するには不向きである．そこで，横瀬の基本公式を基に，デジタル画像の誘導場を計算するモデルがある¹⁾．
　深水，吉田らが指摘しているように²⁾，横瀬の４つの場の基本公式は電磁気学的には誤りである．横瀬は単に電磁気学（ビオ・サバールの法則）のアナロジを利用して，自己の心理実験結果を一般化式を作ったと考えられる．ここでは，横瀬の場の公式をより一般化した計算方法について述べる．
　まず，横瀬の一番目の場の基本公式を純粋に解釈すると，点 P からの距離を積分していることから，ビオ・サバールの法則ではなく，誘導場の強さは単純なクーロンポテンシャルであることがわかる³⁾．実際に Eriksson は誘導場の強さが距離r の逆数 1/r で表されることを心理実験から示している⁴⁾．図１のように，n 個の曲線が点 P につくる場を考える．点 P から各曲線 j(j = 1, 2, ..., n) 上の任意の点 s までの距離の関数を f₁(s)，f₂(s)，.....，f_n(s) とおく．
　誘導場はクーロンポテンシャルであるから，場の大きさは距離の関数 f_j(s) の逆数を曲線上の各点について積分したものになる．また，点 P の場は各曲線 j がつくる場の重ね合わせだから，次式で表される．

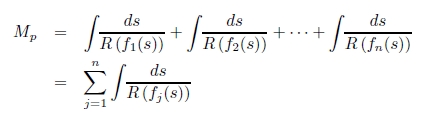
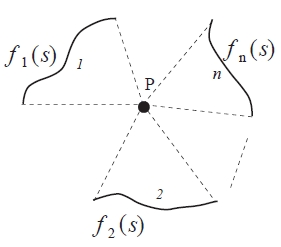
図1　視覚の誘導場の基本はクーロンポテンシャルである

　次に，白黒２値のデジタル画像における誘導場を計算する．パターンの外郭を構成する画素を点電荷と仮定し，それらがつくるクーロンポテンシャルの集積から，デジタル画像における誘導場の分布を計算する． 図２ (a)のように n 個の点列から構成される曲線 f(s) によって点 P に視覚の誘導場が形成されるとする．曲線を構成する各点を正電荷１の点電荷と仮定し，点 P から曲線 f(s) 上の点 i までの距離を r_i とする．点 P における誘導場の強さ M_p を次のように定義する．

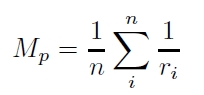
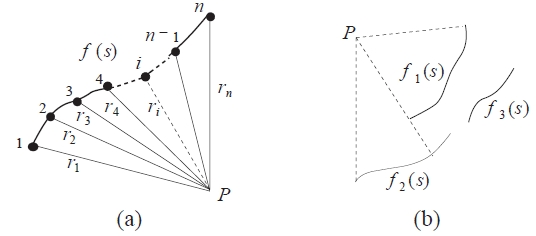
図２　デジタル画像における視覚の誘導場の計算

　曲線が複数ある場合，点 P における誘導場の強さは個々の曲線が点 P につくる誘導場の和になる．　上の式において，誘導場の「遮蔽」を考慮して，点 P から見える部分のみの和をとるという制約条件がつく．例えば，図２ (b) の曲線 f₁(s) に遮蔽されて点P から見えない曲線 f₂(s) の一部と曲線 f₃(s) の和はとらない．なお，デジタル画像では，点 P から見える有効な画素を見つける走査が必要である．中島らのニューラルネットのモデルのポテンシャルの式⁵⁾も　r_i の逆数である点では同じだが，デジタル画像の場合，走査は画素が有限というデジタル画像の性質（画素の連結性）のため，走査する場所，向きにより見つかる画素の密度が変化する．したがって，上の式のように走査対象の画素数 n による規格化 (1/n) を行うことで単位画素あたりの場の強さを求める．

●　計算例

　図3 (a) は，このデジタル画像の誘導場の式で計算した誘導場の例である．図の「Ａ」周辺に等高線状に分布しているのが誘導場の等ポテンシャル線で，中央から外に行くほど場の強さは弱くなり 0 に近づく．数字は場の強さを示す． 図3 (a) の「場」の分布の形状・強さは，横瀬が行った四角形や三角形など，図形の角付近に関する誘導場の分布の心理実験結果と一致する．一方，図3 (b) は遮蔽条件がなく，画素全てを正電荷１の点電荷と仮定した静電場の例であるが，「場」の分布は全体的に丸く心理実験結果と異なる．

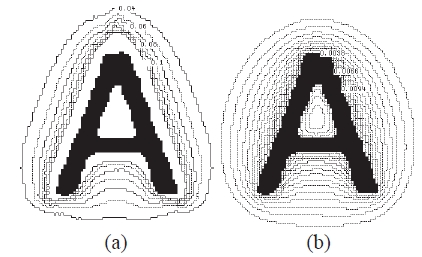
図３　誘導場と静電場の違い

　図4 は，正方形，三角形，Landolt 環の誘導場を計算した例である．図4 の例も含め，図形の角周辺の誘導場が他の部分の誘導場に比べて形状や密度などが急激に変化している．一方，視力はLandolt 環の切れ目の幅の逆数で表されるが，図4 からその切れ目の周辺の誘導場が急激に変化している．このように誘導場は図形周辺に図形の輪郭を形どるように一様に分布するのではなく，図形を特徴付ける角や切れ目といった部分の周辺に変化が生じることがわかる．また，図形の内部の場も計算できる．深水，吉田らの行った純粋な静電場の計算では計算できないが，このデジタル画像の誘導場の式では計算可能である．

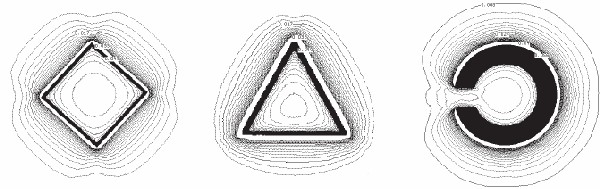
図４　誘導場の計算例：正方形，三角形，Landolt 環

　デジタル画像の誘導場の式を用いることにより，図形パターンのビットマップが得られれば，原理的に任意のパターンの誘導場が計算できる．例えば，図５のような活字やかすれた手書き文字のようなパターンの誘導場を求めることもできる．更に，図６の文字列の例のように，単独のパターンだけではなく複数のパターンが存在する２次元空間での誘導場も計算できる．また，文字などの図形パターンだけでなく，図７のMüller-Lyer， Kanisza の錯視図形⁶⁾ などの特殊な図形についても誘導場を計算することが可能である。

図５　誘導場の計算例：活字，手書き文字

図６　誘導場の計算例：　誘導場の計算例：文字列

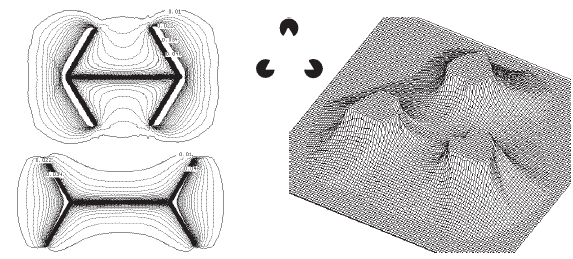
図７　誘導場の計算例：　誘導場の計算例：Müller-Lyer，Kanisza の錯視図形

　このように，横瀬の理論を拡張した，デジタル画像の誘導場の式を用いることで，非常に様々なパターンの誘導場を計算することができる．そして，この式は，深水，吉田らや中島らが側抑制モデルに補正を加えて説明していた，純粋な静電場とは違う遮蔽などの特殊な性質を，点 P から見えない部分を避けるというデジタル画像上での走査を行うことによって比較的簡単に再現している．なお，誘導場による感性評価，文字認識などの応用は，ほとんど，このデジタル画像の誘導場の式が用いられている。

●　視覚の誘導場の場の強さの単位

　以下の理由から誘導場の強さや，文字パターンの類似性の評価で使う，弾性エネルギを無次元として扱うことがほとんどである．
　まず，心理学的に誘導場の強さを表す物理的な単位が明らかにされていない．誘導場の強さは，被験者に呈示した小光点の明るさが基準になっているが，その単位は研究者によってまちまちである．例えば，横瀬は誘導場の強さを小光点の明るさを決める電圧値⁷⁾，野澤はCRT の階調を決めるプログラムで設定する値⁸⁾，深水，吉田らは照度⁹⁾ を用いている．このように，誘導場の強さを表す単位は統一されていない．
　誘導場の計算においても物理的な単位が定義されていない．横瀬のポテンシャル場の公式では，誘導場の強さの単位は無次元である⁷⁾．例えば，距離の単位がcm なのか触れられていない⁷⁾．一方，深水，吉田の F(1) モデルは距離の単位はmm である¹⁰⁾．しかし，誘導場の強さは横瀬の心理実験結果に近い値になるよう，計算式に補正を加えて無次元化しており，誘導場の物理的な単位は明確に定義されていない¹⁰⁾．デジタル画像の場合，三好らは，このページで紹介したデジタル画像の誘導場の式について，誘導場の強さを正規化しているが，単位については定義していない¹¹⁾．このように，基本となる心理学実験で誘導場の強さの物理的単位が明確になっていないため，誘導場の強さは無次元として計算されている．
　このページで紹介した，デジタル画像の誘導場の計算式における距離 r，n の単位はデジタル画像なので画素数(dot) である．しかし，この「画素数」というのはデジタル画像で仮定する仮想的なもので，実際の長さ（mm など）には対応していない．そのため，デジタル画像上の文字認識で使われる特徴量や距離などには単位はつけない．また，この式による計算や誘導場によるパターンの違いは，それぞれ物理のクーロンポテンシャル，弾性エネルギのアナロジを利用しているだけである．実際にクーロンポテンシャルや弾性エネルギを計算しているわけではない．弾性エネルギのアナロジは最近コンピュータビジョンでよく使われるが，エネルギの単位はつけない¹²⁾．一般に，デジタル画像で計算を行う文字認識やコンピュータビジョンでは，特徴量や弾性エネルギなどを無次元として扱うことが多い ^{13), 14)}．

　以上のように，心理学実験で誘導場の強さの物理的単位が明確化されていないこと，そしてデジタル画像は特徴量やエネルギなどを無次元で扱うことが一般的なため，このホームページでは，誘導場の強さおよび弾性エネルギを無次元として扱った．なお，誘導場の再現や強さの比較ができることを考慮して，実験に使用したパターンの大きさ(dot)，パターンを作成した際の解像度(DPI) などを示すのが望ましい．

参考文献

1）長石道博，視覚の誘導場理論を用いた文字認識の提案　電子情報通信学会技報, Vol. PRU92-46, No.4，pp.7-14, 1992.

2) 深水義之, 吉田登美男, 伊藤明, 小谷津孝明. 電磁気学による横瀬の場の理論的見直し　－景観の図形認識の立場からの解明と評価に関する研究(3) －. デザイン学研究, Vol. 42, No. 6, pp.39-46, 1996.

3) ファインマン著, 宮島龍興訳. ファインマン物理学III. 岩波書店, 1990.

4) E. Sture Eriksson. Field effects and two dimensional form perception. Scand. Journal of Psychology, Vol. 8, pp.218-242, 1967.

5) 中島和樹, 菅沼義昇, 伊藤正美. 心理的ポテンシャル場とニュ－ラルネットによる図形認識. 電子情報通信学会技報, Vol. PRU90-155, pp.79-86, 1990.

6) G. カニッツァ著, 野口薫訳. カニッツァ視覚の文法- ゲシュタルト知覚論-. サイエンス社, 1987.

7) 横瀬善正著「形の心理学」名古屋大学出版(1986)

8) 野澤晨. 小点の消失閾による図形の場の強さの再検討. 日本認知科学会第12 回大会, Vol. PD.6, pp.202-203, 1995

9) 吉田登美男, 深水義之, 野田健一. 横瀬の場の理論の実験的検証. デザイン学研究, p. 61, 1993.

10) 吉田登美男, 深水義之, 白石照美, 伊藤明, 小谷津孝明. 心理ポテンシャルの心理物理的伝達関数の誘導と錯視への応用. ラウンドテーブルNo.28, 日本心理学会第62 回大会, pp. 23?32, 1998.

11) 三好正純, 下塩義文, 古賀広昭, 井手口健. 視覚の誘導場理論を用いた感性にもとづく文字配置の設計. 電子情報通信学会論文誌, Vol. 82-A, No. 9, pp. 1465-1473, 1996.

12) Michael Kass, Andrew Witkin, and Demetri Terzopoulo. Snakes: Active contour models. International Journal of Computer Vision, Vol. 1, No. 4, pp. 321?331, 1988.

13) 石井健一郎, 上田修功, 前田英作, 村瀬洋. パターン認識. オーム社, 1998.

14) 田村秀行監修, 日本工業技術センター編. コンピュータ画像処理入門. 総研出版, 1985.

本ページの原典
長石道博: "視覚の誘導場によるパターン認知の研究", 豊橋技術科学大学博士論文乙第142号 (2000) 　[学位論文]