● 従来の文字の読み易さの定量評価
文字の大きさや間隔などを調整して,文字列を読み易く表示する一般的な方法は未だ明らかにされてい
ない.1つ1つの文字自体が読み易い条件はこれまで数多く明らかにされている.例えば,活字の場合,書
体のデザイン1), 2),紙とインキの明度差3),
可読性と文字の大きさの関連性3), 4),2値よりも階調のある文字が読み易い4)などが明らかにされている.
文字列の場合,文字種・文字の大きさ・文字間隔などを調整することによって,文字列が読み易くなると考えられており,
例えば,仮名は漢字より間隔を詰めても読み易いなどの傾向が示されている5).
また,一般に和文印刷では,文字間隔を文字幅の約半分
に設定,句読点など一部の文字の間隔を詰めることが多い6), 7), 8).
欧文は,例えば隣り合う文字が,NM やVA のように互いに平行かVN のように1つの線が違っているか,VT,AA のように両方の線が輻輳しているかで変えるのが良いとされている8).
このように,特定の文字種を中心とした文字間隔の詰め方など,主観的に決められた文字列表示の経験則
が存在する.しかし,任意の文字種について,どのくらいの大きさの文字をどのくらい間隔を詰めても読み
易いかなどを決める定量的な評価方法は,ほとんど明らかにされていない8).
したがって,読み易い和文の文字列表示を実現するには,任意の文字種について,読み易い文字の大きさ,文字間隔を定量的に導き出す基準や方法を検討する必要がある.
さて,文字列内の個々の文字が読み易い状態とは,個々の文字が醸し出している文字の周囲に波及する視
覚の誘導場が,できるだけ干渉しないような間隔で文字が配置されていることが示唆されている.そし
て,手書き文字の切り出しで述べたように,個々の文字を囲む誘導場の閉曲線が存在し,そのポテン
シャル値が高いと他の文字との分離が難しく,読みにくいことが示されている.また,図形や文字の配置が
均整かどうかについても誘導場を用いて評価できる可能性が示唆されている9).
このことから,誘導場の分布を基準にすれば,人間が判断する文字列の読み易さを定量的に評価できると考えられる.
そこで,最初に文字種,文字の大きさ,文字間隔が異なる日本語の文字列における個々の文字を囲む誘導
場の閉曲線の強さが,人間が判断する文字列の読み易さと関連するか調べ,文字列の読み易さの指標とし
ての妥当性を検証する.次に,文字列の誘導場の閉曲線の強さは,個々の文字が単独に存在する場合の誘導
場の分布から計算により予測できることを示す.
|
● 文字列における視覚の誘導場
【文字列の視覚の誘導場の分布と文字配置】
複数の文字で構成された文字列の誘導場の分布と文字配置の関係を検討する.現在,和文書の大半は横書
き文書で,縦書きは文芸書やはがきなどに限られることが多いため,横書きの文字列について
検討する.最初に,図1(a) の文字列「もやゆよ」の例のように上下に別の文字列がなく,一文字列が単
独で存在し個々の文字が接触しない文字列について検討する.
|
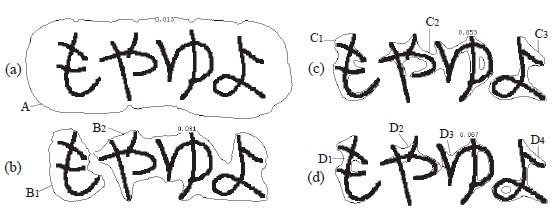
図1 文字列における視覚の誘導場
|
図1 は文字列「もやゆよ」がつくる視覚の誘導場を,図1(a) はポテンシャル値0.013,図1(b) は0.031,
(c) は0.053,(d) は0.067 のように徐々に大きくした場合の例である.
ポテンシャル値が低い 図1(a) の場
合,文字列全体を包絡線のように囲む閉曲線A が存在する.ポテンシャル値が大きくなると,まず,図1(b)
のように「も」のみ囲む閉曲線B1,「やゆよ」を囲む閉曲線B2 が出現する(ポテンシャル値α 0.031).さ
らにポテンシャル値が大きい 図1(c) の場合,「やゆ」を囲む閉曲線 C2 と「よ」のみを囲む閉曲線 C3 が出
現する(ポテンシャル値β 0.053).最後の 図1(d) の場合,「や」「ゆ」をそれぞれ囲む閉曲線 D2,D3 が出
現する(ポテンシャル値γ 0.067).個々の文字を囲む閉曲線のポテンシャル値は文字間隔によって異なっ
ている。例えば「も」は,「や」と「ゆ」の間隔に比べ「や」と離れているので,低いポテンシャル値α で
「や」から分離する.逆に接近している「や」と「ゆ」は,「も」や「よ」に比べ高いポテンシャル値γ でな
いと分離しない.
図1 の例を含め他の文字列の誘導場の分布の観察から,文字間隔が狭く読みにくいと文
字列を構成する個々の文字を囲む閉曲線が最初に出現する際のポテンシャル値は高くなる.すなわち,文
字の間隔によって誘導場の干渉の強さに違いが生ずる.その違いは文字列を構成する個々の文字が分離す
る誘導場の閉曲線の強さで表されると考えられる.
例えば,図1 の場合,3つのポテンシャル値α ,β ,
γ の平均を文字列「もやゆよ」の読み易さの指標に使うことができる.そこで,一般に n 個の文字から構
成される文字列の隣接する i,i + 1 番目(i = 1, 2, ..., n) の文字が最初に分離する誘導場の閉曲線のポテン
シャル値を xi とすれば,文字列全体の読み易さは,次のポテンシャル値の平均 M を用いて評価する.
|
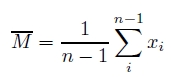
|
【複数の文字列による誘導場の分布】
ある文字列の誘導場の分布に,上下に存在する他の文字列が及ぼす影響を検討するため,印刷に近いコン
ピュータ組版の和文 LaTeX(文書フォーマット jarticle )で作成した複数の文字列を含む画像(320×320
dot,72 DPI)の誘導場を計算し,図1 のようにポテンシャル値を徐々に大きくしながら,各文字列を包
絡線のように囲む誘導場の分布と,各文字列内の個々の文字が分離する誘導場の分布を比較した例が,
図2である.
この例を含め,まず,図2 左側の文字列「般に有効な」「知過程はパ」「的な理論と」のように
各文字列を囲む誘導場がポテンシャル値 0.02〜0.03 程度で現れ,さらにポテンシャル値が 0.04 程度以上に
なると,図2 右側の文字列「知過程はパ」の「パ」,「的な理論と」の「と」「な」などのように文字列内
の個々の文字が分離する.
このように,文字列が複数の場合,各文字列の分離と文字列内の個々の文字の分離は別々に扱うことがで
きるので,分離した各文字列について,図1 の要領で,上式 による文字列の読み易さを評価できると考
えられる.そこで,ここでは文字列の読み易さを,図1 のような単一の文字列について検討する.
|

図2 文字列の誘導場
|
● 文字列の読み易さと誘導場の関連性の検証
上式による誘導場の強さが,人間が判断する文字列の読み易さを説明できることを検証する.ここで
は,いろいろな文字種,文字の大きさ,文字間隔をもつ文字列を被験者に呈示して,読み易さを5段階評
価した心理実験結果と,上式による誘導場の強さの相関を調べた.
最初に,文字の読み易さの心理実験方法について述べる.文字列が単語や熟語を含む場合,可読性が高く
なる単語優位効果10) や,文字列が長い場合に生ずるサッカードなどの眼球運動11), 12), 13) が,文字列の
読み易さの評価に影響することを避けるため,眼を動かさず一目で認識できる日本語の文字数の範囲12)
である5 文字から成る,熟語を含まない無意味な文字列を呈示した.そして,日本語文書の読みに関する
心理実験では,視角を1文字あたり1 ゜11),13) から2 ゜12) 程度に設定すると被験者が読み易いことから,呈示する1文字あたりの視角を2 ゜に設定した.
被験者に呈示した3種類の文字列の基本型を図3 に示す.図3(a) はすべて仮名,図3(b) はすべて
漢字,図3(c) は仮名漢字混じりの無意味な文字列である.これらは,Macintosh 上で,図3(a) のように
一辺の長さが 60 ポイント( 72 DPI )の正方形5個を間隔 0 mm で並べ,それぞれの正方形に正方形の一辺
の長さと同じポイント数の Osaka フォントの文字を,文字の重心と文字が外接する正方形の中心を合わせ
て配列した( 1 ポイント= 0.3514 mm ).以降の実験も解像度,文字のフォントはすべて同じである.
図3 の3つの各基本文字列について,文字の大きさ,文字間隔を変更した文字列を用意する.
まず,図4(a)と同じ要領で,文字の大きさを基本状態( 60 ポイント )の他に 56,52 ポイントの文字列を構成する.
更に,これら大きさの異なる 3 種類の文字列について,文字間隔 0 mm の基本状態の他に,図4(b) のよう
に文字間隔を各文字の間隔を1 mm広げる,または,1 および2 mm詰める.このように,図6.2 の1 つの基本文字列について,3 種類の文字の大きさ( 60,56,52 ポイント),4 種類の文字間隔( -2,-1,0,1 mm )の 12 種類,合計 36 個の文字列を準備した.なお,図3(c) の文字列は,仮名を漢字よりも小さく書くことが多いことを考慮して,「晴」のみ,大きさ 60 ポイントの外接正方形のままとし,他の仮名の外接正方形の大きさを変更した.
図4(c) は,図3(c) の文字列を仮名の大きさを 52 ポイントにして文字間隔を変更した例である.
|

図3 呈示した文字列
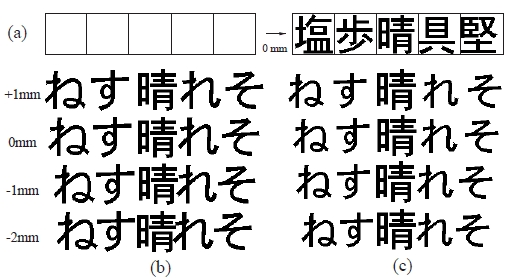
図4 文字の配置と文字列の変更
|
以上のように作成した文字列を,自発光するCRT と反射光を用いる紙の代表的な2種類の方法で,視力
が健常な20 歳代の男子大学院生19 名の被験者に呈示した注1.
CRT はApple 社のMacintosh 用12 インチカラーモニタ,紙は文字列を印刷したボードを使用した.
CRT,紙共に白背景に黒文字である.
各方法共に文字列を1文字(60〜52 ポイント)の視角が 2 ゜程度になる視距離 1.0 m で呈示した.
呈示方法による視距離や被験者の姿勢を変化させないため,CRT と紙の文字列の位置が一致するよう,ボードはCRT の
直前に置き,被験者の顔を顎台に固定した.実験中,暗幕で外光を遮断して照明条件を一定に保った.
そして,文字種,文字の大きさ,文字間隔の異なる 36 個の文字列をランダムに呈示し,時間制限をせずに各
文字列の読み易さを,非常に読み易い 5, 読み易い 4, 普通 3, 読みにくい 2, 極めて読みにくい 1 の 5 段階の絶対評価を口頭で報告してもらった.
これを,CRT および紙による呈示方法別に行った.
評価は,文字列の1文字1文字が何であるか認識するのがどの程度大変に感じるか評価してもらう.読むのが大変に
感じるほど数字が低く(2,1),容易なほど数字は高い(4,5).例えば,文字間隔が充分広い場合,各文字
の認識が容易で読み易い評価になると考えられる.ただし,文字間隔が充分あって文字自体は読み易いが,
文字間隔が余り広いのは嫌いだから読みにくいなどといった個人的嗜好は,読み易さの評価に含めないよう指示した.
事前に,図3 とは文字種が異なる文字列を呈示して評価基準を説明し,それを理解させた後,
本実験を行った.
次に,心理実験に使用する 36 個の文字列を文字列の長さに応じて,256 × 256 dot または320 × 320 dot
の文字画像に変換,誘導場を計算した.そして,図1 と同様の要領で,ポテンシャル値
を0.001 ずつ徐々に大きくした誘導場の分布を観察,i 番目の文字を囲む誘導場の閉曲面が初めて現れるポ
テンシャル値を調べ,上式 による文字列全体の誘導場の強さの平均を求めた.
注1: 実験は,豊橋技術科学大学 情報工学系 臼井研究室にて行われた (1997).
|
● 誘導場による文字列の読み易さに関する検証結果
最初に,心理実験結果の信頼性を検証するため,19 名の被験者をランダムに 10 名と 9 名の 2 群(A,B)
に分け,評価した 36 個の各文字列について,A,B 群ごとに心理実験で得られた主観評価結果の平均を求
め,A,B 群間の相関を調べた.図5(a) は紙に呈示した場合について,横軸にA 群,縦軸にB 群の主観
評価の平均をとった散布図の例である.図中の直線は回帰直線で,相関係数は 0.972 と高い.図5(a) の
例を含め他の紙に呈示した場合,および CRT に呈示して被験者をいろいろな2 群に分けた場合を含め,相
関係数は 0.925 から 0.972(平均 0.948)の高い相関が得られた.このことから,任意の文字列に対する読
み易さの主観評価は,個人ごとにほぼ一定であると考えられる.
次に,文字列の呈示方法の違いによって文字列に対する主観評価の傾向が異なるかを検証した.図5(b)
は 36 個の各文字列について,19 名の被験者全員の主観評価の平均を,横軸に文字列を CRT で呈示した結
果,縦軸に紙で呈示した結果をとった散布図である.相関係数は 0.964 と高い.このことから,文字列に対
する主観評価は,自発光するCRT,または反射光を用いる紙という光源の違いによって大きく異ならない
と考えられる.
|
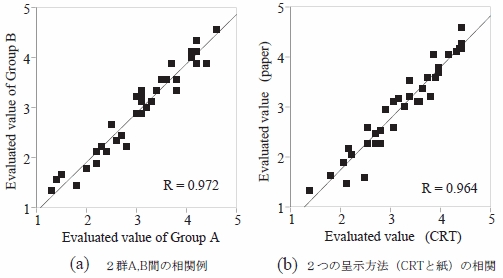
図5 検証結果(被験者群,呈示方法の違い)
|
続いて,読み易さの主観評価結果を示す.表1 は,文字の大きさ,文字間隔の異なる図3 の3つの各
基本文字列について,CRT に呈示した場合の被験者全員の主観評価の平均を示した表である(括弧内は紙
に呈示した場合).図6(a) は文字間隔が 0 mmの場合,図3 の3つの各基本文字列について,横軸に文字の大きさ(ポイント数),縦軸に文字列を CRT で呈示した場合の被験者全員の主観評価の平均をとって
比較したグラフである.
表1 および図6(a) を含めた他の例から,文字間隔が同じ場合,文字が小さく
なると文字列が読み易くなることがわかる.図6(b) は文字の大きさが 56 ポイントの場合,横軸に文字間
隔(mm),縦軸に文字列を CRT で呈示した場合の被験者全員の主観評価の平均をとって比較したグラフ
である.表1 および 図6(b) を含めた他の例から,文字の大きさが同じ場合,文字間隔が広がると読み易
くなることがわかる.また,表1 および 図6 を含めた他の例から,図3(a) のすべて仮名の文字列は,
同じ文字の大きさ,文字間隔の他の文字列より読み易いことがわかる.このように,従来,文字列の状態
の表現に使われてきた文字種,文字の大きさ,文字間隔と文字列の読み易さには関連性が認められるので,
これら3要素の組合せにより文字列のおおよその読み易さを示すことができると考えられる.
|
表1 文字列の読み易さについての心理学実験結果
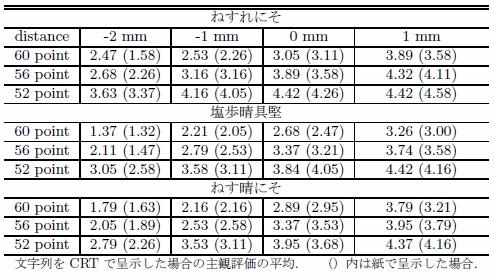
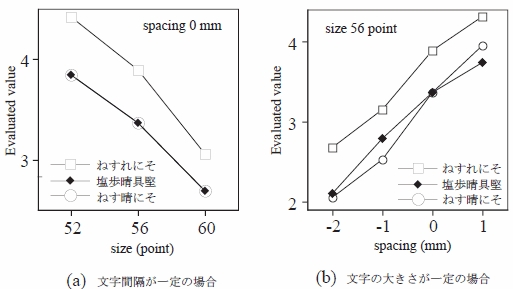
図6 文字間隔,文字の大きさを一定にした場合の文字列の読み易さの違い
|
|
図7 は,横軸に被験者全員の主観評価の平均,縦軸に文字列全体の誘導場の平均を,(a)
は紙,(b) は CRT で文字列を呈示した場合をとった散布図である.なお,計算した誘導場の強さと主観評
価結果はそのままでは相関関係が直線的にならない.そこで,誘導場の強さの常用対数をとり,両者の相関
関係を直線的にした上で相関係数を求めた.図7 より,相関係数は 0.907(紙),0.917(CRT)と高く,誘導場の強さの平均は,文字の読み易さの心理実験結果とよく合致している.そして,誘導
場の強さの平均は,文字種,文字の大きさ,文字間隔が異なる任意の文字列の状態を1つの値で示すことが
できるので,文字列の読み易さを一意に表現する指標に使えると考えられる.
|
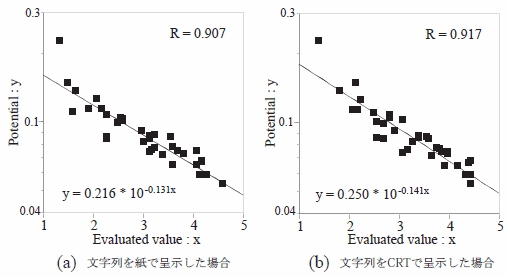
図7 文字列の読み易さと誘導場の強さの相関
|
● 文字列を構成する文字による文字列の誘導場の予測
【2文字間の誘導場による予測】
以上のように,いろいろな大きさや間隔の文字列の誘導場を計算し,誘導場の強さの平均
を求めて文字列の読み易さの心理実験結果と照合すれば,読み易い状態を決定できると考えられる.しか
し,文字列全体の誘導場の計算は,画素を検出するための走査を広範囲な文字列画像につ
いて行う必要があること,また,個々の文字を囲む誘導場の閉曲線の検出において,ポテンシャル値を変化
させながら繰り返し行う必要があるため,計算時間がかかる.
複数のパターン全体が形成する誘導場は,基本的に個々のパターンが形成する誘導場の和である.そし
て,誘導場は遮蔽された部分の影響は受けないので,n 個の文字から構成される文字列における,隣接する
i,i+1 番目の文字間につくられる誘導場の分布は,元の文字列から,i,i+1 番目の文字2つのみを抜き出
した文字列の2文字間の誘導場の分布で近似できると考えられる.すなわち,個々の文字に分離する誘導場
の強さは,隣接する2文字の組合せごとに考えればよい.そこで,最初に文字パターンとして非常に単純化
した円について検討する.
まず,単独で存在する円の誘導場は,円の周辺に同心円状に分布するので,円の誘導場の
強さ m は,円の直径 d と円の中心からの距離 r の関数で表される
(付録:「円における視覚の誘導場の計算式」参照).
m = f (d, r)
図8(a) は,場を計算後,実際に場の画像を計測した直径 64 dot の円の誘導場の分布を,縦軸にポテンシャル値,横
軸に円弧からの距離(円の中心からの距離 r=32 dot)をとって示した例である.図8(a) の例のように,
実際にいろいろな直径の円の誘導場を計測して,関数 f(d, r) を決定することができる.
|
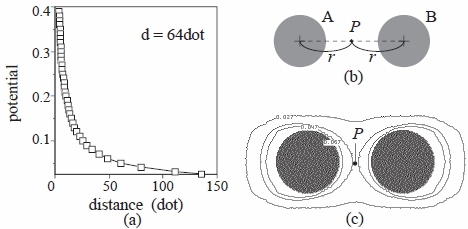
図8 円における誘導場の平衡
|
次に,図8(b) のように,等しい直径d の円 A,B を中心間距離 2r で配置した場合を考える.
円 A,Bは大きさが同じなので,式(6.2) は,円 A,B 共に等しい.よって,図8(c) の誘導場の分布例のように,
中点 P( 円 A および B の中心から距離r)を境に個々の文字を分離する誘導場の閉曲線が存在する.した
がって,円 A,B を個々に囲む誘導場の閉曲線の強さは,中点 P の誘導場の強さ Mp に等しい.円 A,B
が単独で存在する場合の誘導場の強さを m とすると,誘導場は重ね合わせだから,円 A,B を,図8(b) の
ように並べた場合の中点 P における誘導場の強さは,Mp = 2m である.誘導場の強さは距離の2 乗に反比
例するから,円A,B を中心間距離 2r で並べた場合,Mp は,円A(またはB)が単独で存在する場合の円
A(またはB)の中心から距離22r の誘導場の強さに等しい.
Mp = fA ( d, 22r)
円の大きさが異なる場合( dA > dB),円A,B の誘導場の分布は異なる.円A,B が単独で存在する場
合の円の中心から距離 r の誘導場の強さを mA,mB とすれば,誘導場の強さは距離の 2 乗に反比例するか
ら,mA,mB の比の平方根だけ中点 P が,円A の中心から距離r´に移動する.
|
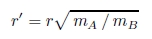
|
したがって,大きさの異なる円A,B を分離する誘導場の強さ Mp は,
Mp = fA ( dA, 22r´)
これらの式から,r´を消去すると,Mp は次式で与えられる.
|
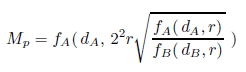
|
図9(a) は,円A の直径が64 dot,円B が48 dot の場合,図9(b) は円A が64 dot,円B が24 dot
の場合について,円A,B の中心間距離(mm)を横軸に,ポテンシャル値を縦軸にとって,個々の文字を
囲む誘導場の閉曲線が最初に現れるポテンシャル値の式による予測と,円A,B を配置して計算した誘導場の実測を比較したグラフの例である.図9 の例を含め,他の大きさの円の組合せも
予測と実測はよく一致している.
このことから,2つの文字の列が個々の文字に分離する誘導場の強さは,
時間のかかる文字列全体の誘導場を計算せずに,あらかじめ求めてある文字が単独で存
在する場合の誘導場の分布から,簡単に求めることできると考えられる.
|
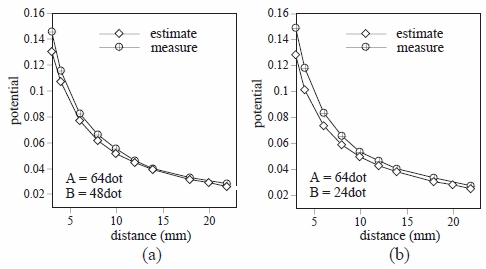
図9 円の誘導場の予測
|
【文字の誘導場の予測】
円の誘導場の分布は円である.文字の誘導場の分布も文字線分に近い部分を除いて,誘導場の分
布の大部分は円で近似できると考えられるので,誘導場の分布をあるポテンシャル値における等ポテンシャ
ル面の面積 A と等しい面積をもつ円の直径(円相当径)dHで表現する.
|
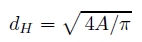
|
図10(a) は,文字種別として文字の大きさが60 ポイントの場合の円相当径(dot)を縦軸に,ポテンシャ
ル値を横軸に示した例である.
円はMacintosh 上で,72 DPI の解像度で作成した.以下の実験でも同じ条件でパターンを作成した.
図10(a) の例を含め,他の大きさの場合も,ポテンシャル値が大きくなる
と円相当径が急速に小さくなる.図10(b) は文字種別としてポテンシャル値 0.16 の場合の円相当径を縦軸
に,文字の大きさを横軸に示した例である.図10(b) の例を含め,他のポテンシャル値の場合も,円相当
径は文字の大きさに比例する.このように,ある文字種の誘導場の強さ m は,文字の大きさ P(ポイント
数)と円相当径 dH の関数で表現できると考えられる.
m = g ( P, dH)
この関係より,図10 のように,いろいろな文字種の誘導場を計算して決定することができる.
|
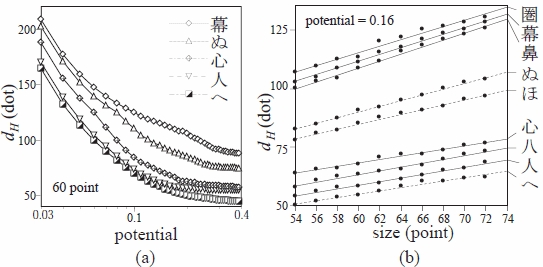
図10 円相当径dH の測定例
|
|
次に,隣接する2文字の位置を外接正方形を基準に定義する.図11(a) のように,2つの文字 A,
B の外接正方形が間隔 d で平行に配列しているとする.文字 A,B の大きさ PA,PB(ポイント数)は,各
文字の外接正方形の一辺の長さと等しい.文字 A,B の誘導場の分布が等しいと仮定すると,文字 A,B の
外接正方形の中心を OA,OB とすれば,円と同様に OAOB の中点 P では文字 A,B の誘導場の強さが等
しくなる.OA,OB から外接正方形におろした垂線の足までの長さを rA = PA/2,rB = PB/2 とすると,
OA から中点 P までの距離 r は,
|
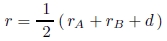
|
|
と表される.実際には図10(b) のように,文字 A,B が同じ大きさでも誘導場の分布は異なるので,
円と同様に文字 A,B が単独で存在する場合,各文字の誘導場の強さに比例して中点 P は移動する.
上式より,移動した中点 P における誘導場の強さ Mp は,次の式で計算できる.
|
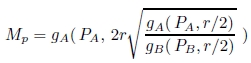
|
|
図11(a) のように文字 A,B の大きさが異なる場合( PA > PB ),一般に外接正方形の底辺はベースラ
インに揃えることが多いので,線分 OA OB は外接正方形と平行ではない.文字 A,B の誘導場の分布が等しい
と仮定すると,OA から中点 P までの距離 r は,
|
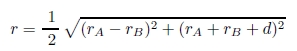
|
|
と表される.実際には,文字 A,B の誘導場の分布は異なるので,図11(a) と同様に,これら2つの式 Mp,r よ
り誘導場の強さを計算する.
|
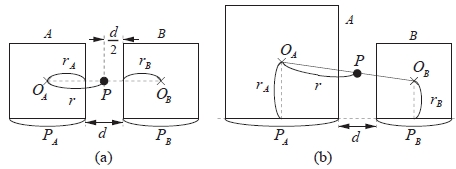
図11 文字の位置関係
|
【誘導場による読み易い文字列予測方法の検証】
図3 の1 つの基本文字列について,図4 と同じ要領で,文字間隔が,-2,-1,0,1,2 mmの5 種類,
大きさが,72,68,64,60,56 ポイントの 5 種類の 25 種類,合計 75 個の文字列を用意した.ただし,仮名
を漢字よりも小さく書くことが多いことを考慮して,図3(c) の「晴」のみ文字の大きさは 72 ポイントに
固定した.文字の読み易さの主観評価実験と同様に,まず,用意した文字列の誘導場を計算,
個々の文字を囲む誘導場の閉曲面が初めて現れるポテンシャル値を調べ,文字列全体の誘導場の強さの平均
を求めた.
次に,図3 の全文字種について,大きさが 72,68,64,60,56 ポイントの文字
が単独で存在する場合の誘導場を計算し,ポテンシャル値が,0.01 から0.001 ずつ 0.399 までの円相当径を
求めて,文字の大きさと円相当径で表わされる,誘導場の強さの関数 m を決定した.
これらのデータを基に,前節で述べた予想式を用いて,
文字 A を i 番目,文字 B を i + 1 番目の文字として個々の文字を囲む誘導場の閉曲線のポテンシャル値を計算し,
文字列全体の誘導場の強さの平均を求めた.
図12(a) は,75 個の各文字列に対し,文字列全体の誘導場の強さの平均について,文字列の誘
導場を実測した結果を横軸に,個々の文字の誘導場の分布による予測を縦軸にとった散布図である.
図中の直線は回帰直線で,予測と実測が一致する理想の傾き 1.0 に近い 0.964 である.
図12(b) は,文字の大きさが 68 ポイントの場合,
文字間隔(mm)を横軸,ポテンシャル値を縦軸にとって,図3(a) の文字列「ね
すにれそ」の「ね」と「す」,および,図3(b) の文字列「塩歩晴具堅」の「塩」と「歩」を個別に囲む誘導
場の閉曲線のポテンシャル値について,個々の文字の誘導場の分布からの予測と実測を比較した例である.
図12 の例を含めた,他の条件での予測は実測に近いことから,文字の誘導場の分布を円相当径で表現す
ることによって,個々の文字を個別に囲む誘導場の強さを計算により予測することができると考えられる.
|
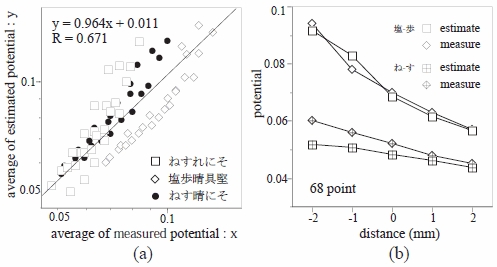
図12 実験結果(読み易い文字列の予測)
|
【読み易い文字列の状態の決定】
図13 は,大きさの等しい同じ文字種を2個以上,等間隔で並べた文字列を紙に呈示した場合,視距離
1 mで,5 段階評価の読み易い状態 4 にするための文字の大きさ(ポイント数)を横軸に,隣接する 2 文字
の中心間距離(mm)を縦軸に示した例である.読み易い状態 4 のポテンシャル値 0.065(図7(a) から計
算)を実現する文字間隔を,各文字種,大きさの文字が単独で存在する場合の円相当径の測定結果,
および,前述の計算式から計算した.
図13,大きい文字は小さい文字より,漢字の文字列は仮名の文字列よ
りも広い文字間隔が必要であることがわかる.これは,表1 および,図6 の例で示された文字列の読み易
さの傾向が,誘導場の分布で説明できることを示している.
以上のように,あらかじめ求めてある個々の文字の誘導場の分布か
ら,時間がかかる文字列全体の誘導場の計算を行わずに,読み易くするための設定すべき具体的な文字種,
文字の大きさ,文字間隔を,任意の文字種の組み合わせに対して,簡単に計算できると考えられる.
|
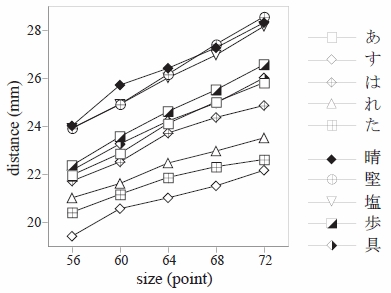
図13 最適な文字間隔の予測
|
● 考察
【誘導場による文字列の読み易さの説明】
図7 の結果から,文字列の読み易さの指標として着目した,文字列の誘導場における個々の文字を囲む
誘導場の閉曲線の強さが,人間による読み易さとよく一致することが示された.すなわち,個々の文字の誘
導場の干渉の強さが文字列の読み易さと関連することが示唆されていたが,干渉の程度は文字列全体の誘導場の強さの平均で表現でき,実際に人間の文字列の読み易さと対応していることが明ら
かになった.このことは,視覚の誘導場は文字の読み易さを説明できる有効な概念であることが示された.
【読み易さの客観的指標】
表1,図6 から,文字列の状態を決める文字種,文字の大きさ,文字間隔によって,文字列の読み易
さをおおよそ推定できると考えられる.しかし,文字列の読み易さを表すには,図6 の例のように,これ
ら文字列の状態を示す3要素の組合せが必要であり,一意に読み易さを決めることは容易ではない.特にフォント,文字飾りなどの要素が増えた場合,文字列の状態の組合せが増大して,読み易さの決定は難しく
なると考えられる.
一方,図7 から,誘導場の強さを用いれば,読み易い文字列の状態を一意に表すことが可能であり,誘
導場の強さは人間の読み易さとよく一致している.すなわち,文字種,文字の大きさ,文字間隔が異なって
も,表示したい文字列の誘導場の強さを計算すれば,文字列の読み易さを誘導場の強さのみで決定できる
と考えられる.このことから,誘導場は読み易い文字列の表示を行うために有効な客観的指標を提供でき
ると考えられる.
【読み易い文字列の状態の決定】
図12 から,文字列の読み易さの指標となる誘導場の強さは,時間がかかる文字列全体の誘導場の計算
をせずに,文字列を構成する2文字ずつの組について,各組の文字種が独立に存在する場合の誘導場の分
布から,計算によって簡単に予測できることが示された.そして,図13 から,表示したい文字列の文字
種の組合せが決まれば,読み易い文字列にするための文字の大きさ,文字間隔が,経験によらず具体的に決
定できる.この方法を用いれば,例えば,プリンタなどの印刷をはじめ,電子ブックなどの携帯端末では
限られた表示面積で見易さをできるだけ落とさず多くの文字を効率良く,また高精細なハイビジョンでは,
より多くの文字をより読み易くするプロポーショナル表示などが可能になると考えられる.
【読み易い文字列状態の予測性能向上のための課題】
図12 のポテンシャル値が大きい場合の仮名などのように,文字の誘導場の分布から予測した個々の文
字を囲む誘導場の強さと実測の違いが,漢字の文字列などと比べ大きい場合がある.これは,文字,特に仮
名は漢字に比べ長いストロークなどの影響により誘導場の分布が複雑になり,円では誘導場の分布が充分
記述できず,誘導場の強さの予測に誤差が生じたものと考えられる.そこで,例えば,等ポテンシャル面
の形状が円で近似できるかを,円形度や複雑度で判断し,複雑な場合,楕円で誘導場の分布を近似して,
個々の文字を囲む誘導場の強さを予測するなどの方法が考えられる.
|
● 文書における複数の文字列の読み易さ
これまで述べた文字列の読み易さは,5文字程度で構成された,無意味な単一の文字列の場合である。
我々が通常,読み書きする,文章として意味のある,複数の文字列の読み易さについて,実際に誘導場で定量評価できることが報告されている16),9),14)。
まず,三好らは,文字と文字の周りの誘導場の分布で,図14の青色の実線のように,場の強さが丁度文字の間で谷になっている部分の場の強さと,その文字列が均整がとれて読みやすいかどうかの判断が一致することを見出した16)。
|

図14 文字列の誘導場の谷
|
|
次に,三好らは,
この文字列の誘導場の谷の強さを指標にすれば,図15(a)のような複数の文字列の文字間隔,行間の最適間隔を決められること,そして,図15(b)のような,外枠の影響を考慮した表札の読み易さが決められることを心理実験で明らかにした9)。
|
図15 評価に用いた,文字列,表札の例 注2
|
|
ここで,文字列の誘導場の谷の強さを,文字列の大きさによって左右されない規格化された強さ E p [ dB ] を導入している。
誘導場の計算対象の図形の大きさを L [ mm ],デジタル画像の分解能を R [ 画素数 / mm ],
任意の点 p におけるデジタル画像の誘導場の強さを M(p) とすると,次式で与えられる。
詳細は文献 9)を参照。
|
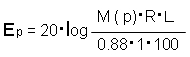
|
|
更に,三好らは,
図16のような,意味のある長い和文の文章について,読み易い文字間隔を,上の式の規格化された強さ E p [ dB ] で
表現する実験式を導き出した14)。この式を使えば,いろいろな大きさの文字列について,読み易い文字組を実際に設計することが可能になる。
|
図16 評価に用いた意味のある長い和文の文章例 注2
|
このように,我々が通常,読み書きする,文章として意味のある,複数の文字列の読み易さについても,
誘導場で定量評価できること,そして,実験結果を基に,文字組を設計することが可能であることが示された。
今後,このページで紹介した誘導場による方法を使い,任意の文字列について,読み易い文字組を設計できるシステムなどへの発展が期待される。
注2:図15,16のフォントは,文献 9) と異なります。
|
参考文献
1) 塚田敢, 湊幸衛. レタリングと文字認識. 心理学評論, Vol.11, pp.140-155, 1968.
2) 和田正信編. 印写工学III 画像形成論, pp.335-340. 共立出版, 1969.
3) 和田正信編. 印写工学VI 視覚と心理,記録, pp. 24-26. 共立出版, 1974.
4) 米山恒雄, 神山忠信, 井沢孝次. 図形パターンの検出感度によるディスプレイ表示文字の評価. テレビ学会誌, Vol.50, No.11, pp. 1768-1774, 1996.
5) より多くの情報を読みやすく〜和文プロポーショナル表示〜 NHK 放送技術研究所 平成9年技研公開内容
6) コマーシャル・フォト編集部. コマーシャル・フォト・シリーズ クリエイターのための印刷ガイドブック1 基礎編, pp.48-49. 玄光社, 1993.
7) 奥村晴彦. LaTeX 美文書作成入門, pp.1-10. 技術評論社, 1991.
8) 大西誠一郎. 異なった文脈の中に位置づけられた文字の認知について. 心理学研究 Jap. J. Psychol., Vol.38, No.1, pp. 25-32, 1967.
9) 三好正純, 下塩義文, 古賀広昭, 井手口健. 視覚の誘導場理論を用いた感性にもとづく文字配置の設計. 電子情報通信学会論文誌, Vol.82-A, No.9, pp.1465-1473 (1999)
10)K. Yokosawa and M. Shimomura. On the role of stimulus similality and segmentation in misprint
detection. In D.Brogan (Ed.), Visual Search 2, Taylor & Francis, pp.369-376, 1993.
11) 池田光男. 眼はなにを見ているか ―視覚系の情報処理― 自然叢書8, 第3章. 平凡社, 1988.
12) 神部尚武. 読みの眼球運動と読みの過程. 国立国語研究所報告, Vol. 85, 研究報告集7, pp.29-66, 1986.
13) 芋阪良二, 中溝幸夫, 古賀一男編. 眼球運動の実験心理学, 第8章. 名古屋大学出版会, 1993.
14) 三好正純,下塩義文,古賀広昭,内村圭一,視覚の誘導場理論を用いた和文文字列の読み易い文字組み設計,映像情報メディア学会誌,Vol.56, No.11, pp.1787-1793 (2002)
15) 横瀬善正著「形の心理学」
名古屋大学出版(1986)
16) 三好正純,下塩義文,古賀広昭,視覚的に均整のとれた図形配置の視覚の誘導場による評価,電子情報通信学会総合大会講演論文集 1998年.基礎・境界, pp.338 (1998)
本ページの原典
長石道博: "視覚の誘導場による読み易い和文文字列表示, 映像情報メディア学会誌,Vol. 52,No.12, pp.1865-1872 (1998)
長石道博: "視覚の誘導場によるプロポーショナル表示の検討, 映像情報メディア学会冬季大会,7-3, pp.115 (1997)
長石道博: ”文字列の読み易さを科学する−視覚の誘導場による文字列の読み易さの定量評価−”,
平成10 年電気関係学会関西支部連合大会シンポジウム, S11-5 (1998)
|
【付録】 円における視覚の誘導場の計算式
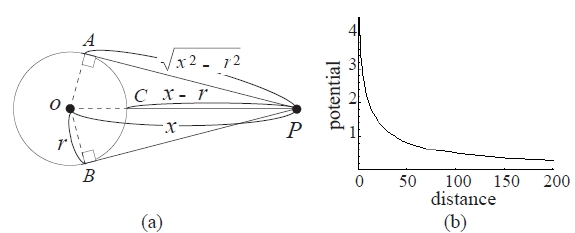
円の誘導場は,円の直径d と円の中心からの距離r の関数で表現できることを示す.付図1(a) のように,半径 r の円の中心 O から
距離 x の点 P における誘導場の強さ Mp は,点 P から円に引いた接線を PA,PB,円と PO の交点を C
とすると,点 P から発した光が当たる円弧 ACB のみで決まるから,文献15) より次式で与えられる.
|
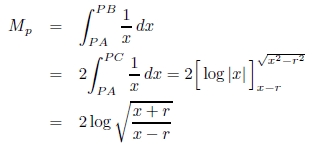
|
|
円の直径d = 2r,x - r = l とおくと上式 は,
|
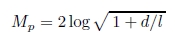
|
|
で表される.付図1(b) は,この計算した d = 64 dot における Mp を縦軸に,円弧からの距離 l を横軸に
とったグラフの例で,d = 64 dot の円を実測した図8(a) の分布に近い.このように,円の誘導場は円の
直径と距離の関数で表される.
|
付図1 円がつくる誘導場
|