2022.08.03
日本の新規感染者数は20万人/日となり、世界第1位となった。もっとも、海外では検査自体が低調となっているから判らない。
日本においても新規感染者数は多分この3-5倍位(70万人位)ではないだろうか?
二次感染可能期間が 3日位だとすると、これが定常化すれば市中感染者数(二次感染可能者数)は、
70万×3≒200万人位となり、これは人口の2%に近い。再感染可能になるまでの期間(獲得免疫有効期間)も大分判ってきて、
これを100日位とすると、このペースで新規感染者数が増え続けた場合には免疫保持者数が70万×100≒0.7億人となるため、
この調子で新規感染者数が更に増え続けるとは思えない。
感染が社会全体に蔓延して永続する場合の、こういう大雑把な話には SIR モデルが適している。勉強がてら計算してみた。
(注:2022.08.20)SIRSモデルというらしい。厚労省の専門家会議資料として、西浦氏がきちんとした解析をしているので挙げておく(資料の最後)。https://www.mhlw.go.jp/content/10900000/000977544.pdf
・S を感染可能な人口割合、
・I を二次感染させることが可能な(感染者の定義)人口割合、
・R を免疫保持者数の人口割合とする。
・・・パラメータとして、
・β を感染速度率、
・γ を感染者が二次感染能力を失う速度率(世代時間の逆数)、
・δ を免疫保持者(感染から回復した人とワクチンを受けた人)が獲得免疫を失う速度率(免疫保持期間の逆数)、
・ε を感染可能な人口に対するワクチン接種速度率(ワクチン接種間隔の逆数)
・・・とすると、
・・・dS/dt = - β・I・S + δ・R - ε・S
・・・dI/dt = β・I・S - γ・I
・・・dR/dt = γ・I - δ・R + ε・S
・・・となる。
・・・こういう循環型の方程式はダイナミクスが複雑になるので、昔から応用数学者が好んで研究してきた。
実際には振動しながら落ち着くようである。下記に数値計算例を示した。
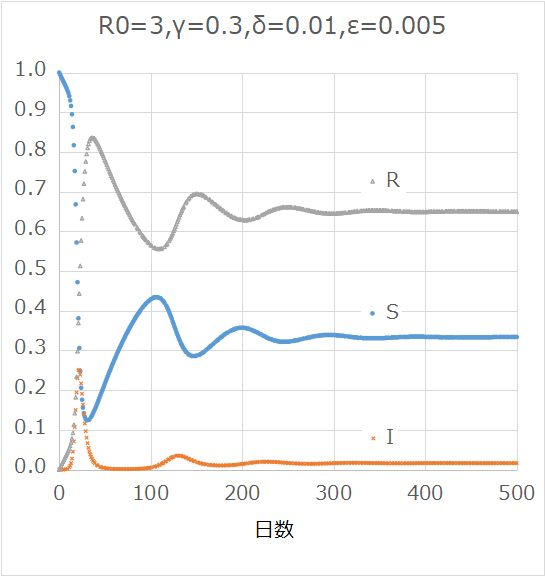
ここではその定常解を考える。感染が定着して定常状態になったとすると、左辺が全て 0 になるから、簡単に定常解が得られる。
・・・基本再生産数 R0 = β/γ と定義する。ここでは獲得免疫効果以外、つまり感染力、感染対策、検査隔離の効果を全て含む。
マスクや換気や外出自粛などの感染対策は βを下げる。検査隔離は γを大きくすると考えればよい。いずれも R0 を小さくする。
・・・R0>1 として、定常解は、
・・・S = 1/R0
・・・I = δ/(γ+δ)・(1-1/R0) - ε/(γ+δ)・(1/R0)
・・・R = γ/(γ+δ)・(1-1/R0) + ε/(γ+δ)・(1/R0)
・・・以下具体的に数値を入れてみる。時間単位は日。βISは新規感染者数の人口比率。
・・・ δ γ R0 ε S I R βIS
・・・0.01 0.3 2 0.01 0.5 0 0.5 0
・・・0.01 0.3 2 0.005 0.5 0.008 0.492 0.0024
・・・0.01 0.3 3 0.01 0.333 0.011 0.656 0.0032
・・・0.01 0.3 3 0.005 0.333 0.016 0.651 0.0048
実際上 I が問題となる。その内の一定割合が重症化・死亡するからである。ワクチンを定期的に接種し続けることになるのだろう。。。
この場合、感染を終わらせる条件は、
・・・ε/δ > R0 - 1
ということになる。
ワクチンの有効性が100%でない場合には、ε がそれだけ縮小される。つまり、ε はワクチンの有効性÷接種間隔ということになる。SIR モデルでは、効果そのものと効果の持続性を一体化して緩和係数にまとめていると考えれば良い。
感染して二次感染可能性が無くなっても、獲得免疫が完全でない場合には、γI の全てが R に入るのではなくて、一部が S に戻るように方程式を変えるべきだろう。
感染の定常状態における感染者数人口比率 I をパラメータとして、R0 と ε の関係を求めると直線になる。下図に示した。
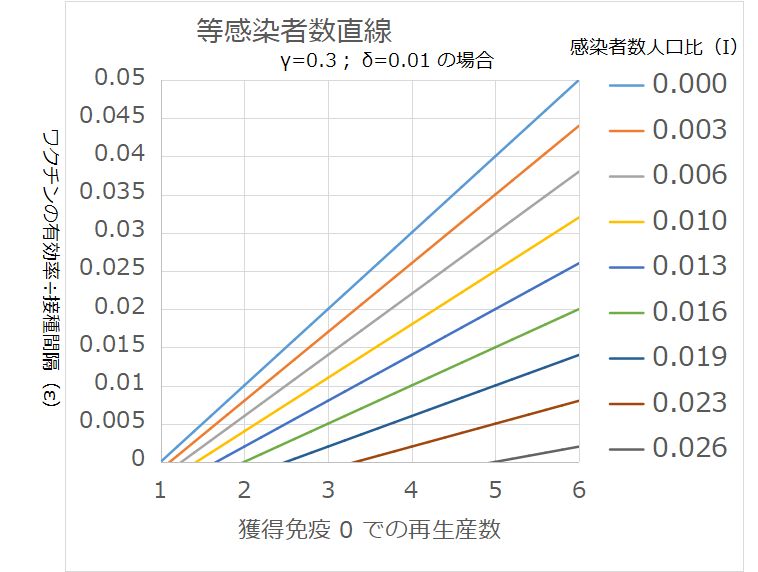
問題はこの感染症において、現状の感染対策で R0 がどれくらいか?ということである。それを求めるためには、現状での実効再生産数 Rt を求めて、獲得免疫保持者数比率を推定しなくてはならない。Rt は簡便には、新規感染者数の発症日毎の推移を移動平均して、潜伏期間だけ前に移動させて分母とし、そこから世代時間だけ後に移動して分子とし、割り算すればよい。獲得免疫保持者数は、ワクチン接種者数が日毎にあれば、そこから過去100日程度の積算、あるいはワクチン失効関数の重み付き積算で推定できるだろう。感染者数からも得られるから、これらを足し合わせれば良い。もちろん、ランダムサンプリングで実際に抗体検査をしてもよいだろう。
● ところで、SIRモデルのパラメータをどうするか?についてはよく考えなくてはならない。
パラメータの時間依存性が無い場合には初期感染者数が exp(λt) の形をしており、λ=β - γ という関係が使えるが、
2つのパラメータは一義的には決まらない。γ は一般的には、医学的知見から推定される。
1人の感染者が二次感染を起こす確率分布が世代時間分布 g(t) は種々の方法で推定されていて、
それに再生産数 R0 を掛ければ、具体的な二次感染者数の時間依存性が計算できる。
従って、
exp(λt) = R0・∫g(s)exp(λ(t-s))ds : 積分は s=0→∞
という関係がある。例えば、g(s) が s=σ でのデルタ関数であれば、
exp(λt) = R0・exp(λ(t-σ))
となり、
R0 = exp(λσ)
これと、SIR モデルにおける
R0 = β/γ
を同じとすべきであろうから、
β/γ = exp(λσ)
という、もう一つの関係式が得られる。
β を消去すると、
1 + λ/γ = exp(λσ)
右辺を展開すると
1/γ = σ + (1/2)λσ^2 + (1/6)λ^2σ^3 + ・・・
ということになる。
・・g(s) = (1/σ)exp(-s/σ) (SIRモデル)とした場合には、
R0 = 1 + λσ = β/γ
となり、
1/γ = σ
が得られる。
・・・整理すると、まず実測の感染追跡データからは、
(潜伏期間分布と発症間隔分布から推定されて)世代時間分布 g(s) が得られている。
g(s) = σexp(-s/σ) となる場合には、γ=1/σ となり、再生産数 R = β/γ となる。
世代時間分布が δ関数で、s=σ にのみ集中しているときには、
感染者数や新規感染者数の推移が exp(λt) に比例する(λ=β-γ)場合に、
再生産数 R = β/γ の関係を保つためには、
1/γ = (1/λ){exp(λσ) - 1} = σ + (1/2)λσ^2 + (1/6)λ^2σ^3 + ・・・
が成り立つ必要がある。
一般的な g(s) の場合にはこれらの中間になるであろう。
ところで、再生産数 R = β/γ というのは、SIRモデル内部での話であるので、
必ずしもこの関係を使わなくても良いだろう。
λ は一般的には経時変化するのであるが、γ がそれに依存するというのは本来おかしい。
(感染係数 β の経時変化よりも、検査隔離による γ の経時変化を主と考えればそうなるのであるが、
現実の観察からはとてもそうは思えない。)
むしろ、γ = 1/σ に固定しておいて、β = λ - γ を維持すべきであろう。
この時、経時再生産数 Rt は(1近傍、つまり λ が 0 近傍を除いては)SIRモデル内部では計算できないが、
上記、1/γ の表式(g(s)の関数形に依る)を使えば計算可能である。