2023.11.14; 2023.11.21に GAN を追加した。2023.12.03に 自己回帰モデル、正規化フロー、拡散モデルを追加した。

『ディープラーニングを支える技術 ２』岡野原大輔著

第３章 深層生成モデル

3.1 生成モデルとは何か

また図については元のサイトを参照の事。

VAEについては、最初の生成モデルであり、基本的なものらしいので、詳しく勉強したが、他は概要を知っただけである。

3.2 VAE（ニューラルネットワークを使った潜在変数モデル）：variational auto-encoder

ここで、見つけた別の資料、『オートエンコーダ（自己符号化器）とは？』であるが、この資料によると、オートエンコーダーとは、要するに主成分分析の非線形版らしい。

＜＜＜＜＜＜ 上記からのコピーである。これは MATLAB の宣伝の為のページであるので著者は明示されていない。

● オートエンコーダ（自己符号化器, autoencoder）とは、ニューラルネットワークを利用した教師なし機械学習の手法の一つ。次元削減や特徴抽出を目的に登場したが、近年では生成モデルとしても用いられている。データ（ベクトル）を（ニューラルネットのような）非線形変換器に入力して、次元を少なくした出力を得る。この出力を別の非線形変換器に入れて、今度は次元数を最初に戻して出力を得る。

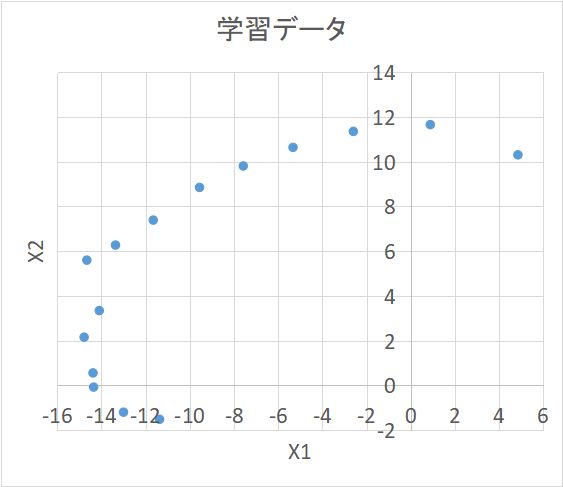
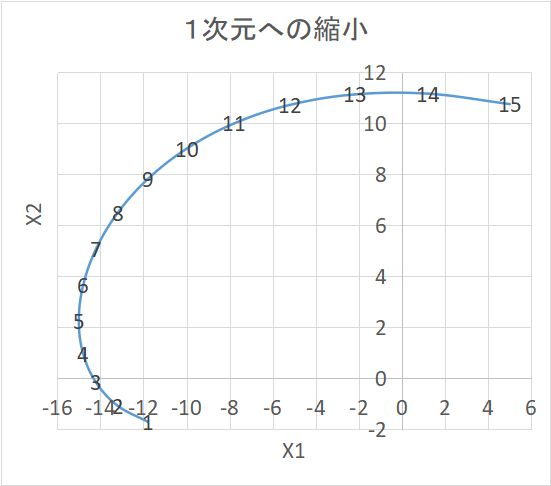
    オートエンコーダの学習は、基本的には、入力データと一致するデータを出力することを目的とする教師なし学習であるが、変形版として教師あり学習とすることもできる。オートエンコーダのネットワークは、入力したデータの次元数をいったん下げ、再び戻して出力するという構造になっているため、入力から出力への単なるコピーは不可能で、学習を通して、データの中から復元のために必要となる重要な情報だけを抽出し、それらから効率的に（且つ近似的に）元のデータを生成するネットワークが形成される。こうしてオートエンコーダの前半部分（エンコーダ）は次元削減、特徴抽出の機能を獲得し、後半部分（デコーダ）は低次元の情報をソースとするデータ生成機能を獲得する。学習後、この2つのネットワークは別々に使うことができる。すなわち、エンコーダは特徴抽出器、デコーダは生成器として独立に用いる。

（注）非線形の例として、２次元の学習データから１次元の潜在変数を取り出した例を図示しておく。この実例は潜在変数からノイズを加えて学習データを作り出しているのではあるが。。。X₁ を Z の二次関数、X₂ を Z の三次関数で近似している。
（X₁ と X₂ を関数関係としてみれば、これは Z による陰関数表現ということでもある。）
下記の係数を未知数として、自乗誤差の総和＝Σ (学習データー試行関数値)² を最小化すればよい。
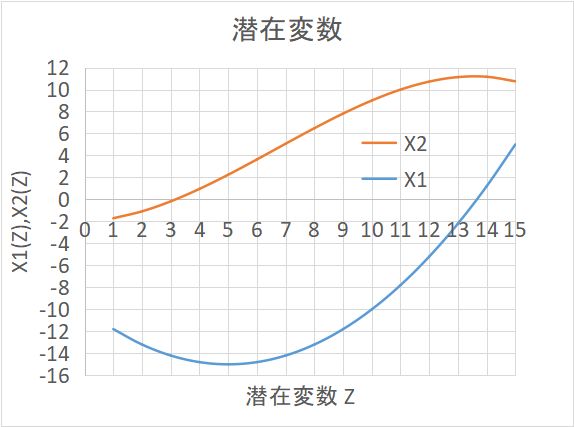
その場合、使う Z の値は何でもよいから、ここでは、学習データの識別番号 1~15 をそのまま使っている。

    X₁ = 0.2*Z² -0.2*Z -10 (+ノイズ );    X₂ = -0.01*Z³ +0.2*Z² +0.1*Z -0.2 (+ノイズ) 。

「生成」というのは、ここでは学習データ点15個以外の任意の点を生成できるという意味である。また、当然ながら、Z を１：１対応で別の変数 Z' に変えても（例えば Z＝ Z'³ とか）同じ事であるから、潜在変数の選び方は一意的ではない。

（注）いつも夢を見るのだが、夢の世界はそれなりに話が連続しているのが面白い。夢の世界は生成 AI によって作られた疑似現実と同じようなものだろうと思う。

      過去の経験が読み込まれて学習された結果、特徴抽出（エンコード）されて、脳神経ネットワーク中に潜在変数空間が出来上がり、情動（記憶の誘因でもある）と結びついている。外部刺激や知性からの抑制を離れた情動によって、その潜在空間の中の任意の点が活性化されて実在空間（といっても感覚中枢）へ射影（デコード）されて、夢が生成されているのだろう思う。潜在空間があまり大きくは変わらないので、時が離れていても話が首尾一貫しているように見える。経験していたわけでもないのに、経験していたかのように感じられるのである。

      潜在変数空間を支配するのは情動であるが、対応する神経細胞の数は膨大なので、心理学で解明されている次元（快ー不快、恐怖ー安心、食欲、性欲、社会的承認欲求、等々）では説明しきれない。結局の処それらは人それぞれなのであって、「美」という言葉で曖昧なままに一括りにするしかないのであろう。だから、美は説明不可能なのだが、それでも言葉で説明することによって、人は注意の在り方を変え、経験を変えることで、結局はその人の「美」が更新されることになる。

● variational（変分法）とは何か？

（注）物理や化学の分野では多体問題が解析的に解けない（答えが数式で厳密に記述できない）場合が殆どであるために、変分法が煩雑に使われる。良く知られた例では、分子内電子の波動関数を個々の電子の波動関数の積で近似して、パウリの原理を満たすようにそれらを線形結合する。この場合、エネルギーを極小にするようにパラメータが調整されるが、どんなに調整しても、本当のエネルギー値は達成されない。しかし、電子状態に依存する分子の性質は殆どがその近似された波動関数でうまく説明できる。
       また、統計力学では、しばしば、状態分布関数を個別粒子の分布関数の積で近似する。個別分布関数を決定するポテンシャル場を平均場と呼ぶ。パラメータは自由エネルギーを極小化するように調整される。これで相転移等も含めて多くの物性が多少不正確ではあっても、説明できる。これらパラメータ変化（つまり関数の変化）による目的関数（上記のエネルギーや自由エネルギー）の変化を変分と呼ぶ。
       機械や建築や土木で使われる有限要素法も偏微分方程式を離散化して変分法で連立方程式に変換している。

・事後確率を最大にする「最大事後確率推定」（argmax__θ{p(θ|X)}＝argmax__θ{p(X|θ)p(θ)}） に分けられる。（MAP: maximum a posteriori）。ベイズの定理から、右辺の {} 内には /p(X) がかかるが、X はサンプル値の組だから、変数ではないので省略できる。右辺の形にすると、p(θ) を事前分布として扱える。つまりベイズ流のパラメータ推定である。

（注）記号の意味：（argmax__θ(・・・) は ・・・を最大化するθという意味の記号；（）内の | の右側は変数ではなくて、条件である。

    p() や q() は 関数 p や関数 q を意味するのではなくて、() 内の確率変数に対する確率分布関数を表す。
                例えば p(X) と p(Y) は別の確率分布関数である。
    また、印としての確率変数は大文字、変数の数値そのものは小文字で表す。）

   ・・・   p(θ|X)p(X)＝p(θ,X)＝p(X,θ)＝p(X|θ)p(θ)：ベイズの定理

・「ベイズ推定」では更に詳しく、最大となる θ だけではなくて、事後分布 p(θ|X) そのものを求める。勿論事前分布 p(θ) を想定してである。

●●ここでまとめておく。

VAE というのは生成AIの一つの代表的な手法である。Variational AutoEncoder である。

    AutoEncoder というのは、機械学習の一つであり、主成分分析の非線形バージョンである。つまり多次元データ X が沢山サンプルとして与えられた場合に、その分布がより低次元の多様体（曲面）にほぼ入るような分布をしていると考えて、その曲面を求める。その曲面内の点が潜在変数で、普通は Z という記号であらわす。元のデータ X から Z への写像（変換、関数）をエンコーダーと呼ぶ。逆に Z が属する曲面に属していれば、それがサンプルから写像された点ではなくても、エンコーダーの逆写像によって、多次元データ空間の対応点が得られる。この操作をデコーダーと呼ぶ。これが「生成」の意味である。

    Variational というのは、変分ベイズ法の意味である。

これらの積分は一般的には広い積分範囲の中に非常に小さな値が散らばっていて、解析的に出来る場合を除けば、精度よく数値計算することが難しい。マルコフチェイン・モンテカルロ（MCMC）法が知られている。

    変分 というのは変分原理に基づいて、パラメータを最適化する方法である。真実の関数形が得られない場合に、それに近い関数形を想定して、そのパラメータを決める。どれくらい真実に近いかという評価指標を最大化あるいは最小化するように、パラメータを決める。ここで使う variational は拡張概念で、パラメータを一つに決めるのではなくて、その確率分布を求める。ここではベイズ法で、 p(θ|X) が真実の分布関数なので、これを試行関数 q(θ)  で近似する。慣例として、p ではなくて、q を使う。

    以上の方法を AutoEncoder に当てはめると、θ についての事後分布ではなく、潜在変数 Z についての事後分布を考えることになるから、θ の替わりに Z を使う。

第１項だけで最大化するのが AutoEncoder であり、Variational となると、第２項が加わる。

変形すると

第２項の意味は、q というエンコーダーと p というデコーダーの逆が確率分布として出来るだけ近くなる、という意味である。

次に、深層学習を使うので、サンプルデータ X からパラメータ φ で決まるネットワーク計算で Z を求める、

（最急降下法による）最適化のためには ELBO を φ で微分しなくてはならない。

                          ＋(1/2)Σ_d(1＋log[σ(φ)²]_d－[σ(φ)²]_d－[μ(φ)²]_d)

第１項において、各 x_n はサンプルデータの画素であり、0 または 1 である。
λ_n が x_n に近ければ {} が最大値 0 に近づく。真逆だと、マイナス無限大となる。
つまり、元の画像を出来るだけ再現するような項となっている。
第２項の 1＋ σ（標準偏差）を含む項は 1 の時に最大で、0 となり、最後の平均値の項は 0 の時に最大で 0 になる。
つまり、標準正規分布（標準偏差＝１ で 平均＝０）において最大となる。

・・・・・・・・・・・・・・・・・・・・・・・・

（脇道の話題）・・・・・・平均場近似・・・・・・
    事前分布 p(Z) に共役形を仮定すると、事後分布も同じ形になる。共役形には、ガウス分布、ウィシャート分布、ディリクレ分布、ベータ分布、ガンマ分布がある。

    q(Z)＝Π_i q_i(Z_i)

    解 q_i ＝ argmin_q_i{KL[Π_i q_i(Z_i)||p(Z|X)]}

データ Z はベクトルであるが、そのベクトル各成分毎の分布 q_i(Z_i) の積で全体の分布 q(Z) が表せるという仮定、というか、そういう分布形を選択する、ということ。強い仮定であるが、そもそも近似なのだから、、。そうすると、式(20)から(32)までを経て、

    解 qi(Zi)＝argmin_q_i{KL[q_i(Z_i)||exp(E_q_j≠i[log p(Z|X))/Const.]]} ：E は期待値を計算するという意味

  つまり、log p(Z|X) を i 以外の成分 j の q_j を重み関数として平均した値（Z_i の関数）の exponent に対して、q_i(Z_i) がどれくらい違うかという KL ダイバージェンス を 最小にするような q_i(Z_i) という関数が解である。なお Const. は q_i に関係しないので、定数とした部分である。KL ダイバージェンスを 0 とすれば、

    log q_i(Z_i)＝E_q_j≠i[log p(Z|X)]＋定数＝E_q_j≠i[log p(X,Z)]＋定数

（注）q_i(Z_i) は電子状態での個別電子状態、分子場近似での分子場下に実現する分子の分布関数に相当する。

（脇道終わり）

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

● MNIST（Modified National Institute of Standards and Technology database）への適用

    これだけではなかなか理解できないので、具体的な例が説明されている。（これはどうも典型的な応用例らしい。）入力データは、MNISTからの手書き0～9までの数字の画像データセットで，6万枚の訓練データと1万枚のテストデータから構成される。MNIST では全ての画像には正解ラベルが付与されているため，画像を入力として受け取りラベルを出力する識別モデルの評価に利用することもできるが、ここでは，VAE を識別モデルとして利用するのではなく，VAE を教師なし学習して「潜在空間の構成」を詳しく観察する、という事で、イメージを掴むには良い例だと思う。

・入力データ X はベルヌーイ分布で近似される（生成される）ことにもなる各画素の白黒値である。次元 N＝画素数。

・潜在変数 Z は D 次元に設定する。単に縮約された次元という意味。D=2 とすると中身が表示しやすい。D を大きくすればより正確な表現になる。

・ p(X,Z;θ)＝p(X|Z;θ)p(Z)： p(Z) が事前分布。

・ p(X|Z;θ)＝Bernoulli(λ(θ))： λ は N個のセルのベルヌーイ分布パラメータ（黒となる確率）を並べたベクトルである。

                   λn(θ) は DNN パラメータ θ によって求められた n番目画素の白黒確率である。

・p(Z)＝N(0,I)： 独立した分散=1の正規分布の積。なお N(平均ベクトル,分散行列) は正規分布を意味する。I は要素1の対角行列。

（注）つまり、D次元空間における単峰分布である。０ から 9 までのどれかに対応しているということではなくて、全体をそう近似しているだけである。具体的には、φ を決めて X から Z を求めて、Z の分布から平均値と分散を計算する。本当は正規分布かどうか判らないのだが、それを強引に正規分布と見なすという意味である。

各画素の白黒確率（画素 n が黒となる確率が λ_n で、白となる確率が 1-λ_n）は、

・p(X|Z;θ)＝Π_n{λ_n(θ)^x (1 - λ_n(θ))^(1-x)}

変分下界(9)を計算すると、下記第１項がサンプル画像とデコード画像を近づける意味を持つ。

                         n は １～N、d は 1～D

あとはプログラムの説明に移っているので、中身は判らない。φ と θ について、上記の L() ELBO を最大化するのであるから、∂λ_n(θ)/∂θ、∂μ(φ)/∂φ、∂σ(φ)/∂φ が各イテレーションにおいて計算できればよい。λ_n や μ や σ は多数のサンプルによる計算の集計結果であり、それぞれのサンプルの計算において微分の表式が得られている（誤差逆伝搬法）のであるから、確かに計算可能だろう。

（注）僕がなかなか理解できなかったのは、X→Z→X' というサイクルにおいて、個々の→で伝達されるのは、DNN の計算結果そのものではなくて、多数のサンプル計算を集計した結果を人為的な確率分布に無理やり当てはめてそのパラメータが伝達される、というやり方に違和感があったためである。個々の X がどの Z に変換されて、それが元の X と一致するかどうかには関心が無いということだろうと思う。しかし、X→Z と Z→X' は X と X' の確率分布関数が近くなるという意味では整合性が採られているので、X ≒ X' となる。

         結果の解析を見ると、D が２次元の空間中にサンプル中の各 X に由来する Z をプロットしていて、それらが各 X に付与されたラベル（0 ～ 9 数字）毎にまとまっている。学習に際して、データ X に対して潜在変数 Z が、φに応じて、推定されるのであるが、この Z をそのままデコーダーに渡すのではなくて、全てのデータから得られる Z の平均と分散を計算して、その正規分布からランダムに Z を選択してデコーダーに渡すのである。実際にはエンコードされる Z の分布は拡がっているのだが、この「正規化」によって、Z の分布が中寄せされる。いわば潜在変数の空間をぼんやりとした円周内に強制的に閉じ込めている感じになる。同じようにラベルを付けた Z 空間の各領域内においても、場所によってデコードされる数字画像（X）の形が違ってくる。また、領域が近い数字画像同士は視覚的に似ている。領域境界付近ではどちらの数字かが判別しがたい。多分脳の視覚野の最後のあたりには、こんな地図が出来ているのだろうと思う。これは実際に画像や Z空間をスキャンしてデコードされる数字画像を表示した動画で見た方が判ると思う。

（注）確かに、世界の現実データを人間の脳が受け取り、それを解釈するということは、その解釈結果からの現実への働きかけによって情報のサイクルを作ることとは切り離せない現象なのである。また、こういうことが可能なのは、そもそも世界の現実データが構造を持っていて、次元の縮約が可能だからである（吉田民人の言う「物質・エネルギーのパターン」）。VAE はその学習方法こそ違え、脳の基本的な機能の重要な側面を捉えているといえるだろう。勿論、まだ母親の胎内にあって、脳神経が軸索を伸ばし始めた頃にすら、何らかの「初期条件」として神経結合定数があったのであるから、「本能」というものは認めざるを得ないだろうが。。。

＞＞＞

（追加）VAE については、もうすこしざっくりとした解説もある。

において、p(Z|X,θ) は真の事後分布なので定数である。そこで、KL[] ＝0 とするように q(Z)＝p(Z|X,θ_old) として固定し、 L[q(Z),θ] （ELBO）＝Q(θ,θ_old) を最大化するように、残りの θ（log(p(X,Z|θ) の θ）を選ぶ。θ が更新されるので、再度 q(Z) を更新する、、、この繰り返し。X と θ_old から p(Z|X,θ_old) が計算できるように確率変数 Z を設定することが鍵となる。

その時は巧妙な方法だと思っただけであるが、一般性のある方法のようである。以下、見直してみた。

・BackProjection での、観測確率変数 X は発症者数（Y(t)）で、これはパラメータ μ(t) のポワッソン分布とした。

・この μ(t) は過去の感染者数に発症時間分布 f(d) を掛けて積算した数で決まるのであるが、その感染者数自身はまたパラメータ λ(t) のポワッソン分布に従う確率変数である。この λ(t) がここで推定すべき θ である。

・N(t,d) から、μ(t)＝Σd N(t-d,d) として、μ(t) が決まる。つまり、λ(t)：θ を与えれば、確率変数 Y(t) :X と N(t,d) :Z とは、μ(t) を介在として結びついている。これが p(X|Z,θ) ＝パラメータ μ(t) のポワッソン分布である。

・この N(t,d) の期待値（＝ポワッソン分布パラメータ）＝λ(t)f(d) を推定するには、ある時刻 t+d での発症者数（Y(t+d)）に寄与する N(t,d) の比率が判ればよい。それを、試行解 λ(t)_old （上記の θ_old）から計算する。Y(t+d) の期待値＝Σi λ(t+d-i)_old f(i) であるが、観測値 Y(t+d) だけから最尤推定されるその期待値は Y(t+d) そのものである。従って、＜N(t,d)＞＝Y(t+d)・λ(t)_old f(d)/{Σi λ(t+d-i)_old f(i)} と推定される。（＜・＞は期待値の記号。）

・＜N(t,d) ＞が推定出来たら、未知数としての λ(t) をパラメータとして、疑似観測値 N(t,d) を実現するようなポワッソン分布の尤度（上記の Q(θ,θ_old)）が決まる。下記の L である。

       logL＝∑(t=1:T)∑(d= 0:T-t) {＜N(t,d)＞log(λ(t)f(d)) - λ(t)f(d)}

本来は ＜N(t,d)＞は N(t,d) なのであるから、未知数 λ(t) を含んでいるのであるが、これが λ(t)_old に固定されている為に計算が簡単になる。（注：統計力学の分子場近似で言えば、λ(t)_old が周辺分子に由来する中央分子へのポテンシャルパラメータである。）

・ logL を λ(t) （上記の θ）で最大化することで、更新された λ(t) が得られる。（注：同上で言えば、中央分子の熱平衡状態を計算して、それを使って周辺分子による新たなポテンシャルパラメータを求めることに相当する。）

・θ について尤度の対数を微分するときに、θ_old が定数として扱える為に、単純な表現となる。その代わりに、θ と θ_old が充分近くなるまで、計算を繰り返す必要がある。

3.3 GAN（敵対的生成モデル）

このモデルは2014年に提案されたもので、もっぱら類似画像の生成に使われている。VAE に比べるとより「創造的」であるので重宝されているが、反面失敗することもあるらしい。
取っつきやすいサイトがあった。
『最初のGAN（Genera tive Adversarial Networks）』（たびの足袋さん）

生成器には乱数が入る。多分正規乱数だろう。これが潜在変数だから次元は低い。
この生成器の出力は学習データ空間に対応させる。その中の一部の次元を占めることになる。
学習データの方は判別器に入る。その確率分布関数と生成器から出てくる確率分布関数が比較される。
具体的にはどうするのか、これは判らない。
生成器の方は比較結果に対して、それを改善するように学習するが、
判別器の方はそれを改悪するように学習する。
よく判らないのは、判別器の方である。

● 元論文を読むときちんと説明してあった。
I.J.Goodfellow et al. Generative Adversarial Nets（2014年）

z は潜在変数であるが、単純なガウシアンノイズ p_z(z) を採る。
生成モデル G については、潜在変数次元から学習データ次元へのネットワークで、
     G(z;θ_g)：z から 学習データと同じ次元のデータ~p_g を生成する。
判別モデル D については、学習データから 0~1 のスカラーへのネットワークで、
     D(x;θ_d)：これを x が p_g 以外に由来する確率と解釈する。
・D の学習は、xの分布 と p_g を出来るだけ区別できるようにすること。
   つまり、D(x;θ_d) を 1 に近づけつつ、D(G(z;θ_g);θ_d) を 0 に近づける。
   この発想がユニークであり、このモデルの「創造性」の要因となっている。
・G の学習は D(G(z;θ_g);θ_d) を 1 に近づける。

   これらを対数表示で表す（確率分布関数の近さを評価：KLダイバージェンス）。
θ_d については、
１．log(D(x;θ_d)) を学習データ x 総数に亙って平均したものを 0 に近づける（最大化する）。
２．log(1－D(G(z;θ_g);θ_d)) をガウシアンノイズ z で平均したものを 0 に近づける（最大化する）。
θ_g については、
３．log(D(G(z;θ_g);θ_d)) をガウシアンノイズ z で平均したものを ０ に近づける（最大化する）。
あるいは、
log(1－D(G(z;θ_g);θ_d)) をガウシアンノイズ z で平均したものを －無限大 に近づける（最小化する）。

以上の数式表現を統一すると、E を平均操作として、

E_x[log(D(x;θ_d))]＋E_z[log(1－D(G(z;θ_g);θ_d))]

を、θ_d については最大化し、θ_g については最小化する。（もっとも、第一項は θ_g には依存していない。）
この表式が θ_d や θ_g で偏微分できるから、θ_d についてはその正の方向に、θ_g についてはその負の方向に動かしていく。
（注）この２つの項は同じ重みであるが、その必然性は無いように思われる。２項の相対的重みを変えれば（係数を掛ければ）生成器としての安定性が変わるのではないかと思う。
あとはいろいろと数学的な話と実例が書いてある。

（岡野原氏の解説）θ_d についての最適化と θ_g についての最適化は交互に行う。出発点はランダムであるから、θ_g については、偏微分が大きくなるように、E_z[log(1－D(G(z;θ_g);θ_d))] を最小化する代わりに、E_z[log(D(G(z;θ_g);θ_d))] を最大化するそうである。
・VAE での生成器では、生成した Xの確率分布の尤度を問題にするので、Z の平均値にランダムノイズを加えるのであるが、GANではその尤度を問題にするのではなく、識別器に識別させるだけであるから、ノイズを追加しなくても良い。このことで生成される結果がより鮮明なものとなる。また、識別器の精度が高くなりすぎると、評価関数の偏微分が非常に小さくなる領域が広くなって最適化に失敗するので、適度に精度を落とすということである。結構微妙な手加減が必要なようである。

（以下、あまり深入りする気がないので、岡野原氏の本に戻る。言語生成モデルについては別途勉強する予定。）

3.4 自己回帰モデル

  時系列データに対して線形モデルとしたものが自動制御で使われているが、時系列である必然性は無い。
  同時確率を条件付確率の積で表現し直しただけであると考えることができる。
  n個の確率変数 x₁,x₂,,,,x_n についての確率密度関数を

      p(x₁,x₂,x₃,,,x_n)=p(x₁)p(x₂|x₁)p(x₃|x₁,x₂)p(x₄|x₁,x₂,x₃)・・・p(x_n|x₁,x₂,x₃,,,x_n-1)

  として、n個の確率密度関数の積で表現する。これ自身は近似ではない。
  VAE や GAN に比べて確率分布をより詳細に最適化できる（尤度が高い）。
  基本的には順序を追って計算されるために、並列処理が難しいので、計算時間がかかる。
  しかし、それを克服するようなスキームが発明されている。
  Causal CNN、Pixel CNN
  ：CNN（畳み込みネットワーク）に使われると、順序が先のセルは参照しないので、かなり並列化ができる。
  Dilated CNN：k層目は kだけ離れたセルしか参照しない。こうするとかなり遠く離れたセルの影響を取り込める。
  ：WaveNet という音声データ生成モデルに使われている。
以上が岡野原氏の説明であるが、これだけではさっぱり判らない。
（注：ChatGPTも自己回帰モデルの一種であり、Transformer を使っている。ここでは触れていない。）

A. van den Oord et al.: WAVENET: A GENERATIVE MODEL FOR RAW AUDIO (2016)
（要旨：DeepLの訳）
    本稿では、生のオーディオ波形を生成するためのディープニューラルネットワークであるWaveNetを紹介する。このモデルは完全確率的かつ自己回帰的であり、各音声サンプルの予測分布は以前のすべてのサンプルに条件付けされる。それにもかかわらず、1秒間に数万サンプルの音声データを効率的に学習できることを示す。音声合成に適用した場合、WaveNetは最先端の性能を発揮し、人間のリスナーは、英語と北京語の両方で、最高のパラメトリックシステムや連結システムよりも有意に自然な音であると評価する。単一のWaveNetは、多くの異なる話者の特徴を等しく忠実に捉えることができ、話者のアイデンティティを条件とすることで、話者を切り替えることができる。音楽をモデル化するために学習させた場合、WaveNetは斬新で、しばしば非常にリアルな音楽断片を生成することがわかった。また、WaveNetを識別モデルとして用いることで、音素認識に有望な結果が得られることも示す。

Xi. Chen et al.: PixelSNAIL: An Improved Autoregressive Generative Model (2018)
（要旨：DeepLの訳）
    自己回帰生成モデルは、画像や音声のような高次元データを含む密度推定タスクで最良の結果を達成する。そこでは、リカレントニューラルネットワーク（RNN）が、前のすべての要素を条件として、次の要素に関する条件付き分布をモデル化する。このパラダイムでは、RNNが長距離依存関係をどの程度モデル化できるかがボトルネックであり、最も成功したアプローチは因果畳み込みに依存している。長距離依存性を扱うことも不可欠であるメタ強化学習の最近の研究からヒントを得て、因果畳み込みと自己注意を組み合わせた新しい生成モデルアーキテクチャを紹介する。本論文では、得られたモデルを説明し、大規模なベンチマークデータセットにおける最新の対数尤度結果を示す： CIFAR-10（1次元あたり2.85ビット）、32 * 32 ImageNet（1次元あたり3.80ビット）、64 * 64 ImageNet（1次元あたり3.52ビット）。我々の実装はanonymizedで公開される予定です。

3.5 正規化フロー

    生成器を可逆微分可能変換で表現する。つまり x＝f(z) と書いて、

    p(x)＝p(z)|det(dz/dx)|

とすれば、確率密度関数 p(x) が定義できるから、変換 f について最尤推定すればよい。
p(z) としては、何でもよいが、計算しやすい正規分布を使う。
問題は f(z) であるが、逆変換も容易でなくてはならない。
f(z) の例として、Affine Coupling Layer が知られている。

L.Dinh et al. NICE: Non-linear independent components estimation (ICLR,2015)
（要旨：Googleの訳）
    我々は、非線形独立成分推定 (NICE) と呼ばれる、複雑な高次元密度をモデル化するための深層学習フレームワークを提案します。これは、優れた表現とは、モデル化が容易なデータの分布を持つ表現であるという考えに基づいています。この目的のために、データの非線形決定論的​​変換が学習され、変換されたデータが因数分解された分布に従うように潜在空間にマッピングされます。つまり、独立した潜在変数が得られます。この変換をパラメータ化することで、ヤコビアン行列式と逆変換の計算が簡単になりますが、それぞれがディープ ニューラル ネットワークに基づく単純なビルディング ブロックの構成を介して、複雑な非線形変換を学習する能力を維持します。トレーニング基準は単純に正確な対数尤度であり、扱いやすいものです。先祖からの不偏なサンプリングも簡単です。このアプローチにより 4 つの画像データセットに対して優れた生成モデルが生成され、修復に使用できることを示します。
https://qiita.com/exp/items/dafadf2d1e60ea1d79ae に解説がある。

3.6 拡散モデル

    岡野原氏が専門としている分野らしい。

    観測データ x₀ にノイズを少しづつ加えていく。データの次元は変わらない。それを順に x₁,x₂,,, と表す。
    式で表すと、

    q(x_t|x_t-1)=N((√(1-β_t) x_t-1, β_t I)

となる。N は正規分布を表す。I は対角行列で対角成分が全て 1 の行列である。
ひとつ前のデータ x_t-1 を一様に（微小比率 βt だけ）減少させておいて、それに減少分のノイズを追加した結果得られる確率密度関数を表す。√(1-β_t) x_t-1 の中心として、 β_t I だけぼやけている確率分布である。これを繰り返せば、最終的には ノイズ分布 N(0,I) に収束する。
    逆にノイズ分布からスタートして、少しづつ観測データを再現していくプロセスを学習させるのが拡散モデルである。その学習の手段として多層ニューラルネットワークを使う。式で表すと、

    p(x_t-1|x_t)=N(μ(x_t,t;θ),Σ(x_t,t;θ))

である。これを逆拡散過程と呼ぶ。ここで、μ と Σ をパラメータ θ を持つ多層ニューラルネットワークで計算し、拡散過程の各ステップでの対応するデータに合わせこむのである。
    全体の構造は VAE に似ているが、VAE における認識モデル（x→z） がここでは単純に少しづつノイズを追加していく、という固定プロセスに置き換えられているので学習の必要が無い。また多数のステップ毎に生成モデルを積み重ねているのであるが、認識モデル側が各ステップで同じなので、生成モデル側も共有できる。これを一気に最適化するには、VAE を同じく、ELBO を最大化する。式で書くと、

    E[logp(x₀)]
    ≧ Eq[log{p(x_0:T)/q(x_1:T|x₀)}]
    = Eq[logp(x_T)＋Σ_(t≧1) log{p(x_t-1|x_t)/q(x_t|x_t-1}]

T は t の最後、つまり正規ノイズ段階を表す。各時刻において log{p(x_t-1|x_t)/q(x_t|x_t-1} を最大化すればよい。つまり、個々の拡散過程で変化した確率密度関数を逆拡散過程でできるだけ元に戻そうとしている。

    Jonajan Ho 等は、μ(x_t,t;θ) と Σ(x_t,t;θ) に対して表現を工夫した。
Ho et al. Denoising diffusion probabilistic models (NeurlPS, 2020)

（要旨：Googleの訳）

非平衡熱力学からの考察に触発された潜在変数モデルの一種である拡散確率モデルを使用した高品質の画像合成結果を提示します。私たちの最良の結果は、拡散確率モデルとランジュバン力学によるノイズ除去スコアマッチングの間の新しい関係に従って設計された重み付き変分限界でトレーニングすることによって得られます。また、私たちのモデルは、自己回帰復号の一般化として解釈できる漸進的非可逆解凍スキームを自然に許容します。 。無条件 CIFAR10 データセットでは、インセプション スコア 9.46、最先端の FID スコア 3.17 が得られました。256x256 LSUN では、Progressive GAN と同様のサンプル品質が得られます。私たちの実装は、この https URLから入手できます。

     Σ(xt,t;θ)=σt² I、σt＝βt or σt＝(1-α(t-1)/(1-αt)βt
     μ(xt,t;θ)＝(1/√αt){xt - (βt/√(1-<αt>))ε(xt,t;θ)}

ε は今のデータとの差分であるから、加えられたノイズそのものを推定しようとしていることになる。
    スコアベースモデルというのがあって、これは対数尤度の入力データ x についての微分をスコアとして、これを学習するモデルである。このモデルと拡散モデルは同等である。（この辺は全く判らない。。。）
    ノイズを含んだ画像からノイズを取り除く「超解像度」モデルとしても使われている。
    アニメーション業界でかなり使われているらしい。