運動方程式の解き方

物体の運動を解明するには運動方程式

ma=F

を解けばよい。

Δv=a･Δt　　Δx=v･Δt

であるから、

時刻tでの速度v(t)、位置x(t)から、時刻t+Δtでの速度、位置を求めるには、

v(t+Δt) =v(t) +F/m･Δt　　x(t+Δt) =x(t) +v･Δt

として求めればよい。(オイラー法)

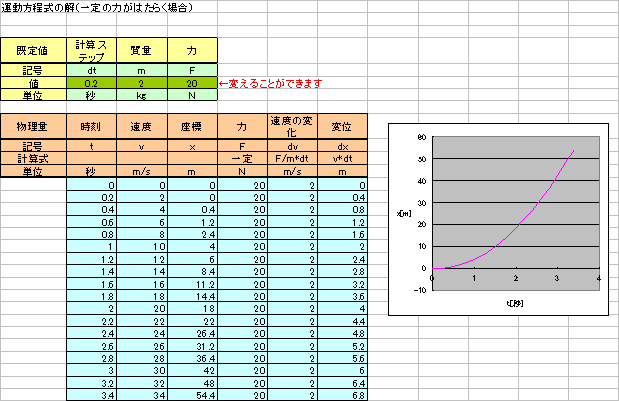
（１） F が一定の場合(等加速度直線運動)

eq_simu1.xls ････････････download

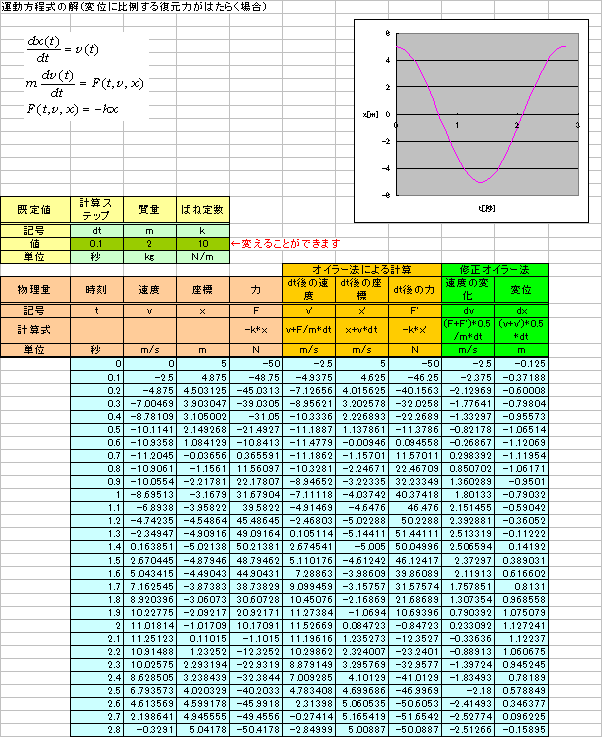
（１） 変位に比例する復元力がはたらく場合F=-kx

　これを解くと、単振動になるが、オイラー法では計算とともに誤差が大きくなるので、修正オイラー法を用いています。

v(t+Δt) =v(t) +0.5･(F(t)+F(t+Δt))/m･Δt　　x(t+Δt) =x(t) +0.5･(v(t)+v(t+Δt))･Δt

eq_simu2.xls ････････････download

---

nozomu Home Pageへ戻る

このページの感想をお寄せください。
nozomu@asahi-net.email.ne.jp

---