K57.森林内の開放空間の風速
著者:近藤 純正・菅原 広史・桑形 恒男
森林内の林床に日射が入り込む開放空間内における風速観測から、開放空間の広さと
風速の低減率の関係を求めた。これは、気候観測所における平均気温の上昇量
(日だまり効果)の見積もりと、観測所の環境保全の指針を作成する際の資料
として活用する。本章では、新たに露場の風通しを表す「露場通風率」を導入した。
(完成:2012年3月30日)
本ホームページに掲載の内容は著作物であるので、
引用・利用に際しては”近藤純正ホームページ”からの引用であることを
明記のこと。
更新の記録
2012年1月1日:作成開始
2012年1月28日:骨組みの作成(図表は未完成)
2012年1月29日:表57.1に大久保公園と防風林N の観測値を追加
2012年2月4日:北の丸公園、防風林S、総合公園などの観測値を追加
2012年2月4日:57.5節「観測値の補正」の一部を加筆
2012年3月4日:図57.3、図57.6、57.4節「熱線風速計の検定」の一部を追加
2012年3月15日:熱線風速計の誤差のことを追記
2012年3月30日:表57.1の(3)に sonic2 を追加
目次
57.1 はしがき
57.2 理想的な観測露場
57.3 林内の開放空間における風速
農環研露場
筑波大学圃場
自然教育園内の3か所
平塚市内の公園6か所
東京の新露場(北の丸公園内露場)
57.4 熱線風速計の検定
(1)廊下を歩いて検定
(2)超音波風速計との比較観測
参考:気象業務法第9条の検定の対象となる検定の合格基準
57.5 観測値の補正
熱線風速計の指向性による誤差
農環研風速計の変更による風速比の補正
57.6 まとめ
参考文献
資料
57.1 はしがき
晴天日中の森林内の日陰の気温は低いが、切り開かれた日当たりのよい開放空間では
森林外の風通りのよい市街地よりもさらに高温となる。これは、森林内では風速が弱く
「日だまり効果」によって、地温や気温が異常に上昇したものである。気温は地表面
付近の風速に大きく依存する。
地上(高度1~2m程度の高度)における風速は何によって決まるかを考えてみよう。
前章「K56.風の解析ー防風林などの風速低減域」では、
防風林などの風下の風速について検討した。幹層の葉面積密度が小さく幅の薄い
防風林では風上から通り抜けてくる風があるが、幅が十分にある森林では「葉面積指数
ah と個葉の抵抗係数の積 c 」によって風下の風速が決まることを示した。
森林内の開放空間では、風下側にも樹木があり、その樹木の風上側に相当している。
風下側にある樹木の影響はどの程度あるか?
諸物体の風上側において、風速が自然風速の95%になる風上距離は、森林の場合は
樹高 h の5倍~10倍程度、円柱の塔などでは半径 r の5~6倍程度である。
図57.1(右図)は半径1mの円筒状の海洋観測塔周辺における風速の水平断面図である。
破線は非粘性のポテンシャル流による分布図である。風上側でも、円柱の半径(1m)
の5~6倍の範囲まで風速の減少域が広がっている。
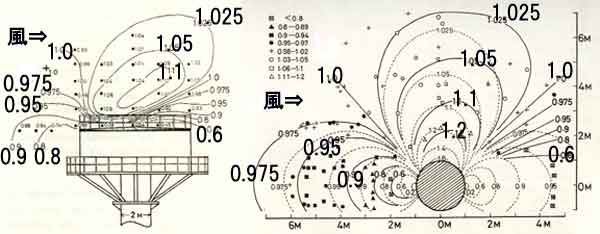
図57.1 海洋観測塔の周りの風速分布、風は左方から吹く場合。
(左)塔の屋上部の鉛直断面図(海面から19~27mの範囲)、
(右)塔中心部の直径2mの円柱部の水平断面図(海面上10m)、
実線は測定風速の等値線、破線はポテンシャル流を仮定したときの計算値。
(「身近な気象」の
「M16.海面バルク法物語」の図16.3に同じ;Kondo and Naito, 1972, より転載)
これらのことを考慮して、森林内の開放空間における地上風速を観測する。すなわち、
本研究では森林内の開放空間のほぼ中央に近い場所で風速を観測し、開放空間の広さと
風速低減率の関係をもとめる。林外の風速が弱いとき林内は微風になり、風速計では
正しい観測が難しいので、林外が比較的強風の時に観測を行う。
微風時は、場所による空気の密度差(気温差)などによって、ごく局所的な対流(
水平・鉛直)が生じており、林外と林内、上空と下層は無関係の風が起きているので、
森林の内外・上下間の風速の違いについては資料の解析から省く。
現実の開放空間は、水平方向に一様でなく複雑であるので、場合によっては空間の
中央付近の数か所で風速を測り、それらの平均を高度2mの代表風速とする。露場で
観測される気温のうち日だまり効果は、露場周辺の100m程度の範囲の地表面・地物の
影響によることを意識して観測しよう。
風速の観測精度:
風速観測の精度は5~10%でよい。なぜなら、試験地の森林は一様でなく、開放空間の
半径や平均樹高の評価には10%程度の誤差を含むからである。本章では開放空間内
の風速が基準の風速(測風塔の観測値)に対する低減率を求めるのだが、その際の
測風塔の風速についても必ずしも理想的な条件での観測値でなく、5~10%程度の誤差
(あいまいさ)をもつ。
こうした誤差(あいまいさ)と同程度の精度で風速観測を行う。風速センサーは
熱線風速計を用いる(輸入販売元の(株)エムケー・サイエンティフィクの熱線風速計
DT-8880)。風向に対する指向性があり、風向変動が大きいときは弱めに観測される。
この誤差は通常は10%以下である。しかし、林内の開放空間のように風向変動が大きい
場所では、誤差が大きくなる。10分間ごとの平均風速を測る際に風向が30°以上も
大きく変化することに気づいたときは、その都度センサーの向きを変えて観測し、
指向性による平均風速の誤差を少なくする。
後掲の図57.7によれば、風向変動の標準偏差が30°以上では、熱線風速計の指向性
による誤差が10%以上となる。
備考:熱線風速計の指向性による平均風速の誤差
この章の観測を行う時点では、熱線風速計の風向に対する指向性が明らかでなく、
近似的に ”cos-law” に従うものとして、図57.7を作成してあった。その後2012年
3月になって、検定装置を作り熱線風速計の指向性を実験的にもとめた結果、
平均風速の観測誤差は cos-law と少し(±5%)違うことがわかった。詳細は
「K58.熱線風速計の検定と指向性」の表58.1を参照のこと。
57.2 理想的な観測露場
気象観測所の露場は樹木や建築物などで取り囲まれている。しかし、建物の場合は
大きな変化がなければ「日だまり効果」によって平均気温が上昇したとはしない。
樹木の場合は成長し、露場の風速(高度2m付近)が弱まり、日だまり効果を起す
ことになる。気温は年々変動が激しく、気温観測のみから日だまり効果によって
何℃の気温上昇があったかを見出すことは難しい。その代わりに、露場風速の経年変化
から日だまり効果の発生を知ることは容易である。
そこで、モデル露場(理想的な露場)を基準にして、現実の露場風速が弱いかどうかを
判断する。モデル露場とモデル測風塔の風速計高度を次のように設定する。
測風塔高度:zA=20m(対象とする気候観測所・試験地の測風塔高度=
10~35m)
露場風速計高度:zr=2m
露場と周辺の粗度:zo=0.003m(露場外も広大な芝生とする)
モデル露場の風速は、平均状態(大気安定度が中立、強風時)を想定し、風速鉛直分布
の対数則から、
風速比:Ur/UA=ln(zr/zo) / ln(zA/zo)=0.74±0.06
ただし、
UA:測風塔高度の風速(m/s)
Ur:露場の風速(m/s)
上式の右辺に±0.06を付けたのは、現実の測風塔高度が10~35mであることを考慮した
場合のばらつきの範囲を示すものである。
気候観測所や試験地について調べ、風速比が0.74±0.06に近いほど理想的な露場
(日だまり効果の小さい露場)と見なすことができる。その度合いを次式によって
「露場通風率」と定義し、露場の適否を決める重要な成績とする。
風速比=露場風速(高度1.5~2m)/測風塔風速(高度10~35m)
露場通風率(%)=風速比 / 風速比理想値
次節で得られる試験地の諸要素を表57.1に示した。表中の平均風速比は弱風時を除く
全風向の平均値である。熱線風速計によって求めた風速比の補正および露場通風率の
補正は未補正のままとする。その理由は「まとめ」の章の最初に記す。
表57.1 露場の諸パラメータの一覧表(熱線風速計による観測は未補正)。
風速比と露場通風率は延べ90分間以上の観測時間による。
農環研露場と筑波大圃場については2009年の1年間毎時観測による。
露場の広さ=(開放空間の平均的な半径 X) /(周辺の建物含む平均樹高 h)
平均風速比:全風向を含む観測の平均値、または全観測の平均値(未補正)
広さ:卓越風向に重みをつけた全方位角の平均的な X/h
ゼロ面変位 d をもつ測風塔の場合の風速比:Ur/UA=ln(zr/zo) / [ln(zA-d)/zo]
露場通風率(%)=風速比/風速比理想値
露場通風率(補正)(%)=風速比(補正)/風速比理想値
測風塔高度 有効高度 露場風 平均 平均 風速比 露場 同左 広さ
zA(m) zA-d(m) zr(m) 風速比 風速比 理想値 通風率 通風率 X/h
補正 補正
(0)モデル露場 20 同 左 2 0.74 0.74 100 ∞
(1)農環研露場 25.0 同 左 1.85 0.64±0.081 0.58 0.71 90 81 7.7
(2)筑波大圃場 29.5 24.5 1.6 0.46±0.086 0.70 66 7.9
(3)自然教育園 20.0 10.2
水生 2 0.30 0.74 41 4.3
武蔵野 2 0.17 0.74 23 1.4
旧棟跡 2 0.157±0.05 0.74 22 1.3
同上(sonic1) 20.0 10.2 2 0.179±0.037 0.74 24 1.3
同上(sonic2) 20.0 10.2 2 0.233±0.038 0.74 31 1.3
(4)平塚(注1)
桜ケ丘公園 10.0 同 左 2 0.51 0.80 64 8.8
旧露場跡 10.0 2 0.24 0.80 30 1.2
四十瀬川公園 10.0 2 0.30 0.80 38 3.5
大久保公園 10.0 2 0.26 0.80 33 2.5
総合公園 10.0 2 0.39 0.80 49 4.4
防風林内N 10.0 2 0.08 0.80 10 0.15
防風林内S1 13.5 同 左 2 0.09 0.77 21 0.11
防風林内S2 13.5 2 0.08 0.77 10 0.12
防風林内S3 13.5 2 0.10 0.77 13 0.13
防風林内S4 13.5 2 0.10 0.77 13 0.14
(5)湘南海岸公園 13.5 2 0.59 0.77 77 14.5
(6)東京新露場 35.0 23.9 2 0.23 0.72 32 3.1
・旧棟跡(sonic1)は超音波水平二次元平均風速による2011年12月8日~2012年1月7日まで
の期間、30分ごと30分間観測値から評価、ただしタワー風速>2m/s のとき、
空間の端で観測。
・旧棟跡(sonic2)は同上、2012年3月6日~3月22日の期間、
タワー風速>3m/sのとき、空間の中央部で観測。
・旧棟跡は熱線風速計による観測であり、sonic1 に比べて0.88(=0.157/0.179)、
sonic2 に比べて0.67(=0.157/0.233)と小さいのは、指向性による誤差の補正を
していないからである。また、風速は「センサー1-表示部A、逆方向」で主に観測し、
風速が弱めに出ており、これも補正していない。
注1:平塚沿岸の陸上風速 U13.5の風速計高度(13.5m)は平均樹高(11.5m)
よりわずか2mしか上に出ていなく代表性がないので利用しない。その代わりとして、
北寄りの風のときは辻堂アメダスの風速(風速計高度=10m)を陸上の代表的な
「測風塔風速」として用いてある。ただし、辻堂アメダスは樹高 h=10mの防風林北端
から X=17mの距離にあり、NNEの風向に対して X/h=1.7 で観測しており、地域の
代表風速として弱めと見なされる。そのため、平塚の風速比は
過大に評価される可能性がある。
南寄りの風のとき、平塚の沿岸域を代表する「測風塔風速」は平塚沖海洋観測塔の
高度21.5mの風速の0.75倍とする。詳細は次節の(5)「平塚湘南海岸公園」を参照。
注2:露場通風率は、測風塔風速が近傍地物の影響を大きく受けていないとき、
測風塔風速に対して露場風速が大きく落ち込んでいるかどうかを表すパラメータである。現実には、
測風塔の高度が不十分で、近傍地物の影響により測風塔風速が弱めに観測され
ていることもある。このような場合、風速比は大き目であり、露場通風率が見かけ上
大きな値となることがある。それゆえ、測風塔高度が低いとき
は、露場通風率が大きいからといって、露場が理想に近いと判断してはならない。
目安として、露場通風率が概略50%以下は広域を代表する地球規模の気候観測所として
不合格である。都市にある多くの気象台は、露場の露場通風率は50%以下と想像され、
しかも通風率が時代によって変化し地球規模の気候観測所としては適していないが、
都市環境の観測所として必要である。都市には多くの人々が暮らしており、その生活
環境を知らなければならぬ。
露場通風率が50%以上であっても、日だまり効果による気温上昇が0.1℃~0.5℃の
場合は観測値を補正することになる。年平均気温の補正値>0.5℃の場合は、
その補正値に含まれる誤差が0.1℃以上となる可能性があるので、気候観測所としては
不合格となる。
「露場通風率」は気候観測所として露場の適否を決める重要な成績であるが、
最終的な適否は、近傍の地形突起度(山頂、斜面)や平均風速の強弱などを総合して
決めることになる。例えば、平均風速が強い強風地では、露場通風率が多少低くても
日だまり効果による年平均気温の上昇は小さくなるからである。
57.3 林内の開放空間における風速
樹木など障害物までの距離 X が小さい場合は、直接的に X と樹高 hを測定し、
開放空間の広さ(平均的な半径)Xを求める。農環研露場のように障害物までの距離が
50m以上大きい場合は経緯儀(セオドライト)によって障害物の上端の高度角αを
測量して無次元距離(X/h)を求める。無次元距離の全方位の平均値を開放空間の無次元
半径 X/h と定義する。
「無次元距離」と「無次元半径」の意味は同じである。前者は長い防風林のような場合
に用い、後者は四方が樹木・建物等の障害物で取り囲まれている場合の呼び名である。
開放空間のほぼ中央から測った無次元距離の全方位の平均値は卓越風向に重みをつけた
平均値とする。現実の開放空間は複雑であるので、試験地ごとの状況に応じて開放空間
の無次元半径を求める。空間が縦方向に長い場合(例えば、自然教育園の水生
植物園)、風はその方向に流れやすく、時には逆風向となることがある。
hoを測量器の高さ(地面からの目の高さ)、h=ho+h1 とすれば、
tanα0=ho/X
tanα1=h1/X
tanα≒h/X
ここに、α0は障害物の根本と水平面のなす角度、α1は
障害物上端と水平面のなす角度、α=(α0+α1)である。
平坦地の場合、障害物の根本から上端までの角度αを測量すればよい。つまり、
露場風速に影響する障害物の要素について数値的には X も h も必要ではなく、露場の
ほぼ中心(風速測定点)から見た X/h の値が分かればよい。
例えば、α=4°のときはtanα=0.0699、したがって X/h=1/0.0699=14.3(X=100m
ならh=14.3m)となる。
α(°) tanα X/h
1 0.0175 57.1
2 0.0349 28.6
3 0.0524 19.1
4 0.0699 14.3
5 0.0874 11.5
6 0.1061 9.4
X/h > 50 は障害物の影響が及ばない距離であり、1/(tan1.1°)=50、ゆえに α<1.1°
は障害物なしと見なしてよい。風速比(=露場風速/測風塔風速)と開放空間の広さと
の関係(図57.9)から判断すると、必要とする風速比の精度は0.05程度、
αの測量精度は0.5°でよい。したがって、セオドライトの高度目盛間隔1°の内、
0.3°までを読み取れば十分である。
セオドライトは簡易型でよく、本研究では牛方式のポケットコンパス レベルトラコン
(LS-25)を利用する。高度角目盛は1°間隔であるが、望遠鏡気泡管は反射鏡付の
ため、望遠鏡の水準は高精度で設定できる。倍率12倍、視野角は2°40’である。
測量は写真測量と併用して行う。写真は北、北東、東、・・・・・の8方位を撮影し、
セオドライトでは全方位を5~10°間隔で高度角を測量する。試験地の平均的な広さ
(表57.1の右端の列)は、卓越風向に重みを付けた高度角の平均値とする(表57.1
では自然植物園の水生植物園のみ、他は重み付けなしの平均値)。
重みの付け方は、試験地ごとの状況を考慮する。
(1)農業環境技術研究所新露場(農環研露場)
やぐら構造の測風塔の頂上、25m高度に風速計「測風塔風速計」が取り付けられて
いる。その測風塔から南東方向約20mの距離に高度1.85m用の風速計「露場風速計」
が設置されている。露場風速計は、北西風に対して塔の影響を含む可能性がある。
露場は広く、おおよそ125m×(75m~150m)の台形である。測風塔から南の方向に
工場の建物があり、風速に及ぼす影響があるかもしれない。
この露場では、芝生の草刈りが頻繁に行われ、草刈り直後の草丈=0.01mであり、
草丈<0.1mになるように管理されている。前掲の表57.1で示したように、試験地の
中ではもっとも理想に近いことがわかる(露場成績:露場通風率補正=81%)。
農環研の旧露場は庁舎本館南側にあって1980年から2005年まで25年間のデータが蓄積
されてきたが、近年周辺の樹木が成長し、周辺環境の維持が困難となり、2005年4月
から新露場で試験観測が実施され、2006年9月から正式運用が開始された。新露場は
旧露場の南東約340mの位置にあり、観測資料はWebサイトで公開されている
(石郷岡ほか、2006)。
図57.2は風速比の方位角依存性である。風速比は風向が北東~東(16方位の風向
=2~4)のとき小さく、南西~北西(16方位の風向=10~14)の風向のとき大きい。
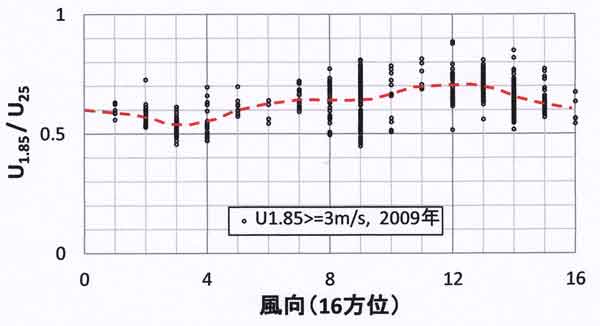
図57.2 農環研露場における風速比の風向依存性。風向は測風塔トップの観測値、
2009年の毎時データのうち露場風速 Ur≧3m/s の場合
(zr=1.85m)。
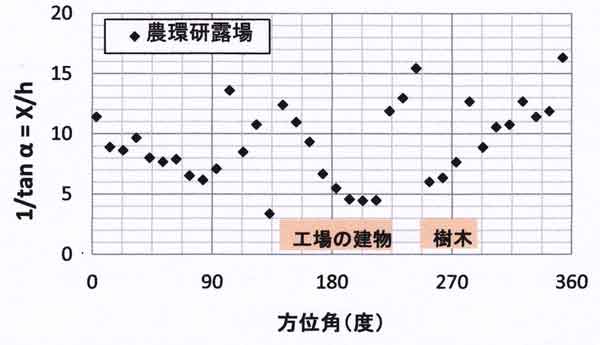
図57.3 農環研露場から見た周辺の障害物までの無次元距離 X/h の方位角分布。
方位角はセオドライトの磁石で測った方位に磁気の偏角西向き7°を補正してある。
図57.3は、塔から見た周辺の障害物(建物・樹木等)までの無次元距離(X/h)と
方位角の関係である。前記のとおり、高度角αは、目の高さから測量した値を地表面
からの高度角に補正してある。
前図57.2と比較しながら、風速(高度25m、1.85m)に及ぼして
いる周辺環境の影響を検討してみよう。
南方向(図57.2では方位8の方向、図57.3では180°の方向)に75mの距離には工場
の建物(高さ=17m、幅=120m、長さ(北西から南東)=330m、塔からの視野角幅=
100°)があり、西方向(図57.2では方位12の方向、図57.3では270°の方向)に110m
離れて視野角幅30°の樹木群(森)がある。
これら工場の建物と樹木群は高度25mの風速を弱めている。
そのため図57.2の縦軸の風速比を大きくする。これら2つの地物の影響を除け
ば、図57.2の縦軸の大きさは図57.3に示された X/h の方位角分布とよく対応している。
すなわち、露場風速計(高度1.85m)から障害物までの無次元距離 X/h(X:水平距離、
h:障害物の高さ)が大きいほど風速比(露場風速 / 測風塔風速)が大きくなっている。
注2:露場通風率をみるときの注意
露場通風率は測風塔風速が近傍地物の影響を大きく受けていないとき、測風塔風速に
対して露場風速が大きく落ち込んでいるかどうかを表すパラメータである。現実には、
測風塔の高度が十分に高くなく、近傍地物の影響により測風塔風速が弱めに観測され
ていることもある。このような場合、風速比は大き目であり、露場通風率が見かけ上
大きな値となることがある。それゆえ、測風塔高度が低いときは、露場通風率が大きい
からといって、露場が理想に近いと判断してはならない。
(2)筑波大学陸域研究センター圃場(筑波大圃場)
直径150mの円形圃場があり、その外側の北西~北東側には施設の建物など、その他の
方向には森林がある。この圃場では、風速や気温など通常の気象要素のほか、熱収支量
の観測が行われている。
圃場の草刈りが実施される年と、生態系の研究目的等で草刈りを行わない年がある。
1993~95年は草刈りされず、その後の数年間も草刈りされない期間があった(三枝信子、
私信)。しかし、最近の数年間は、塔の西側の試験区を除き、圃場の草刈りが年間2回
ほど行われている。
Hayashi(1983)によれば、1978~1980年の夏季8月の草丈は0.5m前後であり、1978年に
高度0.2~4m範囲の風速鉛直分布の観測から求めた地表面の粗度は zo=0.03m
(0.01~0.08m)である。
1981年8月以降の観測資料が公開されている(筑波大学陸域環境研究センター熱収支・
水収支観測データベース)。それら資料から、風速と風速比の経年変化を求め、
図57.4に示した。
高い高度の風速は遠方の地表面の平均的な粗度に依存し、低い高度ほど観測塔の近くの
粗度に依存する。左図によれば、高度29.5mの風速は圃場内の状況よりもそれを取り
囲む森林・建物の外側、塔を中心とする風上3km付近までの扇形範囲の粗度によって
決まる。
一方、高度12.3mと1.6mの風速は、圃場内の粗度と周辺(塔から80~100m)の樹木
等の影響を受けている。風速が長期的に減少しているのは、その樹木の成長を表して
いると思われる。高度1.6mの風速 U1.6 はこの30年間に12%減少している。
1993~2003年期間の U1.6が小さいのは年間の平均的な草丈がその前後に
比べて伸びていたことを表していると考えられる。この傾向は、風速比を表す右図に
よく現れている。
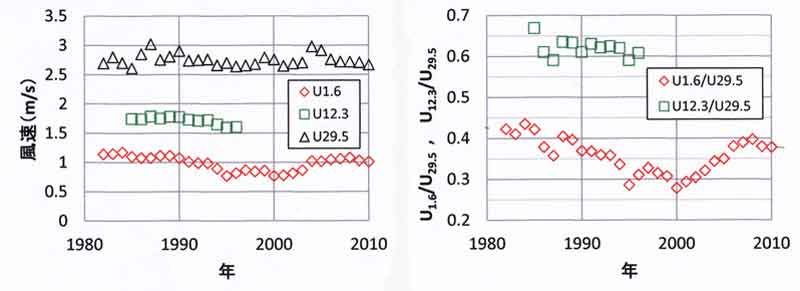
図57.4 筑波大圃場における風速(左)と風速比(右)の経年変化。
山中勤准教授に作成していただいた2009年の毎時観測資料から、風速が比較的強い
とき(U1.6m≧2m/s)を選び、風速比(=U1.6/U29.5)と風向
との関係を求め、図57.5に示した。頻度の多い風向きは北東~東の風、西~北西の風、
次いで南南西である。
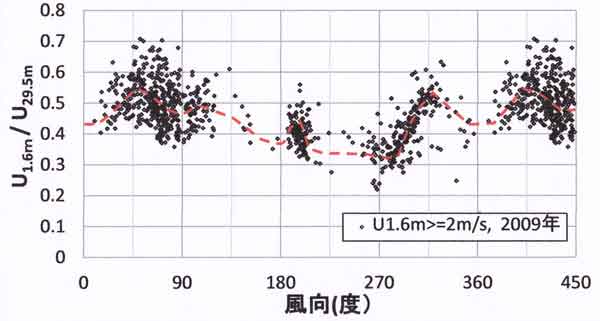
図57.5 高度1.6mの風速の高度29.5mの風速に対する比の風向依存性、2009年毎時
データのうち、強風時(U1.6≧2m/s)の関係。風向は高度29.5mの値で
ある。見やすくするために北~東方向を360~450度に繰り返してプロットしてある。
図57.6は圃場中心の地面から見た周辺の障害物までの無次元距離 X/h (=1 / tanα)
の方位角分布である。高度角αは、目の高さから測量した値を地表面からの高度角に
補正してある。
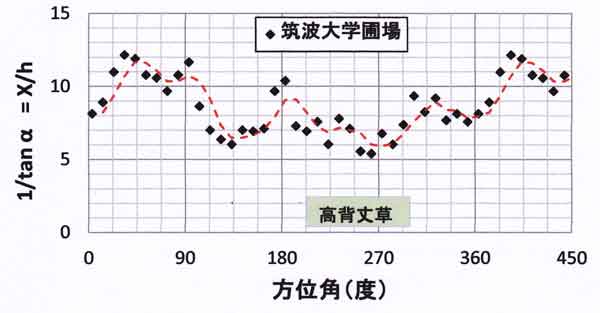
図57.6 筑波大学の圃場中心の地面から見た周辺の障害物までの無次元
距離 X/h の方位角分布、方位角はセオドライトの磁石で測った方位に磁気の偏角
西向き7°を補正してある。180度は南、0度と360度は北方向を表す。見やすくする
ために北~東方向を360~450度に繰り返してプロットしてある。
図57.5と図57.6を見比べてみよう。風速比は風向によって複雑な特性を示しているが、
圃場中心の塔の地面から見た周辺の障害物までの無次元距離 X/h の方位角分布と見事
に一致している。
より詳細に見てみよう。圃場半径(=75m)以遠の外側の障害物(森林、建物)
とは別に、圃場内に残された草丈の高い草地(カヤ)の影響がある。その草地は生態系
の調査のために残されたもので、塔からの方位角=200~300度の範囲、塔から最短距離
の西方向18mの距離にある(図57.6の横軸の目盛りの上に「高背丈草」と記入した
部分)。
図57.5では、風速比は風向=260~290度の最も小さくなっているが、風向=270度の右
方の風向>300度で急激に増加している。
このことは、気象観測露場の環境管理を行う際の教育に役立つ。
露場風速計から18mの距離は、露場フェンスの外側に相当し、フェンスの外側に
草丈1mを越えるような雑草が生えると、露場風速の弱化として現れ、
それによって日だまり効果による気温上昇が起こることになる。
注3:草丈の高い草地の影響
塔の西側(最短距離=18m)に、方位角=200~300度の範囲に草丈約2mの草地(カヤ)
が長期間にわたり残されている。方位角110~160度範囲の無次元距離=5~7と
比べて、西側の方位角=250~290度範囲の無次元距離=5.4~7で、大きな違いはない。
これらの無次元距離は圃場半径75m以遠の樹木によるものである。
いっぽう風速比は、方位角110~160度範囲で0.45前後、方位角250~290度で0.34前後
である。したがって、カヤ草地の1.6m高度の風速に及ぼす影響は0.34/0.45=0.76、
つまり最短距離18mにあるカヤの影響は高度1.6高度の風速を24%前後弱化させている。
(3)自然教育園内の森林内の解放空間(3か所):
東京のJR目黒駅の東、白金台の自然教育園は森林におおわれているが、一部に開放
空間がある。水生植物園、武蔵野植物園、旧事務棟跡の3か所で観測した。1回の観測
は30分間(10分間×3)とし、1か所につき延べ90分の観測結果である。ただし、
タワー風速>2m/sの条件のみを採用した。風速比の平均値は前記の表57.1と後掲の
図57.7に示した。
水生植物園と武蔵野植物園の写真は「K55.日だまり効果の試験地と
観測方法」の図55.14と図55.15に示してある。
(4)平塚の公園6か所(露場跡、桜ケ丘公園など):
神奈川県平塚市海岸にある元・防災科学技術研究所平塚支所の旧露場跡と、海岸から
1.7kmの北方向にある桜ケ丘公園(元の県立平塚工業高校跡地)、1.4kmの距離に
ある四十瀬川公園、2.8kmの距離にある大久保公園、3.1kmの距離にある総合公園、
及び海岸に沿って作られている防風林の中で観測した。
旧露場跡には建物(相模湾海底地震観測施設、マイクロ波収納塔)が建てられ、
現在は狭い空間となり気象観測は行っていないが、環境悪化の代表例として
選んだ。
桜ヶ丘公園の写真は「K55.日だまり効果の試験地と
観測方法」の図55.10に示してある。
四十瀬川公園はJR東海道線の北側の住宅地にある。グラウンドは45m×95m、
その外側10mには樹木が2列(東側は7列)に植えられている。グラウンドを取り
巻く樹高11mの樹木は約7m間隔にあり、それらの中間には樹高5~7mの低木がある。
さらに外側は道路(南と西側は6m、北側は4m、東側は2車線道路)を隔てて、
やや密な2階建住宅であり、グラウンドは全体として森林に囲まれた開放空間と
みなすことができる。
大久保公園のグラウンドはおおよそ50m平方、周囲は樹木に囲まれ、その外側の南と
西は幅員6mの道路、東側にはプールなど、北側には滑り台など公園遊具の広場、
それらの外側は住宅地である。グラウンド中央から方位角10度間隔で測った樹木など
の高度角α(8°~34°に分布、平均21°)を測量した。αは樹木の根本から樹冠上端
までの高度角である。36方位のtanαの平均値は0.394、X/h=1/0.394=2.5である。
総合公園の面積は概略500m平方あり、その中のレストハウスの南側、野外ステージの
ある芝生の広場「平塚のひろっぱ」で観測した。この広場の周囲には樹木が円形状に取
り囲んでいる。その外側にはふれあい動物園や種々の広場・競技場・野球場などがある。
風速の観測地点から樹木の高度角α(8°~19°に分布、平均13°)を方位角5°間隔で
測量した。測量した72方位のtanαの平均値は0.227、X/h=1/0.227=0.44である。
ここで定義した総合公園の広さ X/h=4.4 は自然教育園の広さ4.3に近いが、後者は
縦長であり、全体を見渡したとき、総合公園のほうがはるかに広い印象を受ける。
海岸の防風林の幅は約100mある(主に松、所々に背丈の低い広葉樹)。この防風林の
中には2車線の国道134号線が海岸線に平行して通っている。国道と海岸の間にある
海側の防風林内(林内N)で風速を観測した。林内に”N”を付けたのは、北寄りの風
のときに観測し、測風塔風速は辻堂アメダスを用いたことを指す。
林内 N の防風林の松の樹高は約10mである。この冬に枝切りが行われ、松林の中は散歩
できるほどに整備された。天空を見上げたときの天空率は50%程度である。開放空間の
無次元半径は、便宜的に0.15として風速の観測値をプロットする。
以上の6地点を代表する「測風塔風速」は辻堂アメダスの風速(風速計高度=10m)
を用い、風速>2m/s の条件で、かつ平塚沖海洋観測塔の風速と風向が辻堂とほとんど
同じ(ただし海洋観測塔の風速は2倍ほど強い)ときを採用した。両地点の風向風速が
大きく異なるときは、近くに収束線などがあり風の場の一様性が成り立たない場合で
あるからである。観測は辻堂アメダスの風向がNNEときの結果である。
平塚の各地点での観測は北寄りの風のとき行ったが、防風林のみ南寄りの風のときも
観測した。南寄りの風のときは国道より陸側の防風林内(林内 S )で観測した。
「K55.日だまり効果の試験地と観測方法」の図55.6と図55.7
に示す湘南海岸公園のグラウンドの向こうに見える防風林である。
林内 S の防風林の松の樹高は約11mである。林内には幅1.8mの舗装遊歩道が縦横
不規則的に整備されており、天空を見上げたときの天空率は50%程度である。無次元
半径は便宜的に0.11~0.14として観測値をプロットする。
1回の観測は30分間(10分間×3)とし、1か所につき延べ90分間の観測結果である
(一部には70分間も含む)。
風速比の平均値は表57.1と後掲の図57.9に示した。
(5)平塚湘南海岸公園:
2012年2月1日、冬にしては久しぶりに南西の強風が吹き、防風林Sの観測後に平塚
湘南海岸公園の芝生上でも風速を観測した。この公園の広さは南北130~160m、東西
280mほどある。南西風(海上21.5m高度でも南西風、11時~13時の平均風速18.3m/s)
に対して、防風林から160m(X/h=14.5)の風下で観測した。
観測場所は、「K55.日だまり効果の試験地と観測方法」の
図55.7に写っている、芝生と裸地グラウンドの境にある4段の階段の右方(西)の
ベンチの左方の芝生上2mで風速(90分間の平均8.1m/s)を観測した。
海面上を吹いてきた南西風が防風林を超えて吹く風であり、風向変動は少なく、
海上風に似ていた。
海岸部における陸上13.5m高度の風速「測風塔風速」として、防風林がない時代、
1970年頃の南寄りの海上風速Useaに対する陸上風速U13.5の比(U13.5/Usea=0.75)
を用いる。つまり、次式で推定した。
南寄りの風のとき、平塚沿岸域の測風塔風速(高度13.5m)=0.75×Usea
詳しくは、「K56.風の解析ー防風林などの風速低減域」
の56.3節「防風林植樹前の陸上風速の推定」を参照。
(6)東京の新露場(北の丸公園内露場):
北の丸公園内に開設された新露場は周囲より1.5m高い盛り土、その広さは10m平方、
フェンスの高さは1.4mである。樹木のない範囲(小木除く)の直径は約33m、
(半径は17m程度)である。
新露場の写真は「写真の記録」の「93.東京の新露場」
の図93.2~図93.7に示してある。
東京管区気象台によれば、新露場の開設にあたり、周辺の小木は伐採し、露場面から
周辺の樹木を見たとき高度25°以内、平均18°になるよう背丈の高い樹木は上部を
切りおとしてある。したがって、開放空間の広さはX/h=1/tan18°=3.1とする。
今後は18°を維持するよう管理される。
注4:露場周囲の平均樹高=露場面から見た平均樹高+1.5m=
空間半径17m×tan18°+1.5m=5.5m+1.5m=7mとなる。実際には、露場に近い
樹木は上端を切り落としたため低いが、遠方に見える樹高は平均16m(10~24m)
である。16mは科学技術館屋上の風速に影響する科学技術館周辺一帯の平均樹高で
あり、2011年12月8日の測定値である。
57.4 熱線風速計の検定
一般の気象観測用風速計は高価なので、ここでは安価な熱線風速計を利用している。
これは気象観測用ではないが、便利に作られているかわりに精度が
問題である。仕様書に記された精度は±(5%+1d)となっている。気象測器も
含め一般には、仕様書どうりではないことが多く、うのみにはできない。
(1)廊下を歩いて検定
2012年2月27日の夜、
農環研北棟2階の廊下(幅=2.2m、高さ=2.3m、長さ=230m)で、
熱線風速計を手に持ちセンサーが頭上の斜め右方向45°になる姿勢で歩き、歩行速度
がセンサーに対する相対風速として検定した。5mの序走距離を取り、試験距離=
123.6mを70~80秒間で往復を歩いた。
出力の平均風速に対する真速度(=1.5~1.8m/s)の比は、
(熱線指示値 / 真値)=0.85±0.01
であり、安定した値が得られた。この検定方法は、風速計を静止空気中で移動させて
行うもので、”絶対検定”と名付けてよい。
しかしながら、熱線風速計を持つ人体が動くと、その体積に相当する空気が向かい風
となって熱線風速計に加わっているので、そのぶんを補正しなければならない。
人体の断面積 / 廊下の断面積=0.11
であるので、廊下断面上の平均風速は歩く速度の11%増しとなる。人体の腰のレベル
では11%より大きく、頭上斜め前方では11%より低いとみなされる。実際に、他の
人に何度か歩いてもらって、腰レベル(人体と廊下壁面の中間の位置)と頭上斜め前方
で風速を測定してみると次の値を得た。
腰レベルの風速 / 人体歩行速度=0.13
頭上斜め前方風速 / 人体歩行速度=0.03
参考までに、人体通過後は渦巻きの風速(0.13~0.17)が数秒間続く。この結果から、
頭上斜め前方のセンサーが感じた0.03(=3%)の風速を補正すると、
(熱線指示 補正値 / 真値)=0.85(1-0.03)=0.83
となる。つまり、この熱線風速計は風速範囲 1.5~1.8m/s において、風速真値の83%
の値を示した。
注5: ここで得た上記の比(0.83)は次の章に示す回転式検定装置による検定結果
と比べると、誤差1%の違いで一致することがわかる(「熱線風
速計の検定と指向性の図58.3の「逆方向」のプロットを表す関係、および58.6節
の「歩行による検定」を参照)。
(2)超音波風速計との比較観測
2012年3月1日の11時35分~12時25分にかけて、防衛大学校の地上から47mの高度
において超音波風速計と熱線風速計を並べて比較観測し、
10分間平均風速について5回行い、次の結果を得た。
(熱線指示値 / 超音波風速計指示値)=0.80±0.02
ただし、超音波風速計による平均風速=4.98±0.38m/s
上記比較観測の直後の観測(12時32分~42分):
風向変動の標準偏差=16度
平 均 風 速 = 5.12m/s
風速変動の標準偏差=1.18m/s
次章の「k58.熱線風速計の検定と指向性の図58.3の
「逆方向」のプロットを表す関係、および58.6節の「超音波風速計との比較」を参照
し、補正すると熱線風速計と超音波風速計による風速観測値は6.5%の違いがある。
超音波風速計の仕様書によれば精度は±5%となっており、また、熱線風速計の検定
誤差(指向性も含む)は±3%であるので、6.5%の違いは許容範囲内とみるべきだ
ろう。
参考値
2012年2月28日の14時50分~16時25分にかけて、筑波大学圃場の高度1.6mの
超音波風速計から数m離れた所に熱線風速計を設置して比較観測した。高度1.6mの
超音波風速計に対して観測塔が風上側にあり、観測塔の影響があるかないかのぎりぎり
の風向であった。そのため、正しい比較観測ではないので、参考値としておく。
高度29.5mの平均風向は90~120度(東~東南東)の範囲であり、100度以下のときの
データのみ解析した。全90分(10分間、9回)のうち30分間のみのデータによれば、
(熱線指示風速 / 超音波風速計指示値)=0.826である。この観測では、熱線風速計
のセンサーは大きな風向変動に対して手動で向きを変えた。細かな風向変動に対する
熱線風速計の指向性による補正を仮に図57.7から0.95とすれば、
参考値:(熱線指示補正値 / 超音波風速計指示値)=0.826/0.95=0.87
これは比較観測であり、筑波大学の超音波風速計の誤差も含むが、その誤差は大きく
見積もったとしても、5%以内であろう。
参考:気象業務法第9条の検定の対象となる検定の合格基準
第六条 風速計の合格基準、第三節風車型風速計、第百条風車型風速計の検定公差
風車の直径が15cm以上・・・・0.5m/s または風速の5%、の大きいほう
風車の直径が15cm以下・・・・1m/s または風速の10%、の大きいほう
ただし、微風速計は除く、となっており、
風車型微風速計は・・・・・・・・0.3m/s または風速の5%、の大きいほう。
同上、百三条超音波式風速計の検定公差
上記の風車型微風速計と同じ公差が示されている。
第九十七条の風杯型風速計(カップ式)も風車型と同様である。ただし、風杯の直径
が5cm以上とそれ以下、及び微風速計で3区分されている。
上記は検定の合格基準であり、その後の利用や観測環境によって、誤差が大きくなる
こともある。観測資料の利用に際しては注意すべきである。
57.5 観測値の補正
熱線風速計の指向性による誤差
追記(2012年3月15日):
熱線風速計の正しい指向性は、本章の観測の時点では不明であり、
いわゆる cos-law に近似的に従うものと仮定し、以下に示す
「平均感度」を計算してあった。その後、2012年3月になって、次章
「K58. 熱線風速計の検定と指向性」において、
正確な「平均感度」がわかった。
それでも cos-law の見積もりと大きな違いがないので(±5%以内)、今後、
似た問題が生じたときに役立つので、以下の記述はそのまま
残すことにした。
観測に用いた熱線風速計は指向性があり、センサーの向きと風向が一致する角度0°と
逆向き180°のときは風速を正しく測ることができるが、センサーの向きから風向が
ずれるにしたがって風速を弱めに観測する。その角度のずれ「偏角」をβとすると、
近似的にcosβに比例する感度となる。
それゆえ、風向変動の標準偏差がσ=15°であれば、誤差は3~4%で無視してよい
(「大気境界層の科学」の図3.14)。しかし、林内など風向変動の大きい場所では
風向変動幅σが大きくなるにしたがって誤差は急速に大きくなる。
観測においては、風向を体感・目視によって定め、その方向に熱線風速計のセンサー
を向ける。体感・目視による誤差が、仮に10°あったとしてもcos(10°)=0.985であり、
たいした誤差にはならない。
風向の時間的変動をともなうときの風速の真値に対する割合を次のよう
に定義する。
平均感度=観測風速(熱線)/ 風速・・・・・時間平均値
分母・分子ともに、ある時間、たとえば10分間の平均値を意味する。分子の計算は、
まず、次の瞬間値を瞬間ごとに計算する。
観測風速(熱線)の瞬間値=W(t)×abs[cosβ(t)]
W(t):瞬間 t の風速(スカラー風速:風杯式や風車型風速計の観測値)
β(t):瞬間 t の熱線風速計センサーと風向のなす角度(ラジアン)
abs(絶対値):観測風速(熱線)はマイナスにならないので絶対値を付ける
風向きが逆向きとなり、90°<β<270°では観測風速(熱線)は-90°<β<+90°
のときと対称になりマイナスにならない。 ある長さの時間 t1
(例えば10分間)の平均の観測風速(熱線)は上式の積算値の t1 時間
平均である。
理論的には、風向変動の標準偏差σがあまり大きくなく(σ<20°程度)、かつ頻度
分布が正規分布のときの出力率は近似的に次式で表される(近藤、1982、大気境
界層の科学、式3.54)。
平均感度≒2-exp[ (σ2) / 2 ]
次に、実際の風向変動(厳密には正規分布でない)を用いて計算してみた。
比較的強風が続いた2009年1月10日の12時~24時の12時間(=10分×72)に農環研露場
の高度25mで観測された10秒ごとの瞬間風速 W(t) と瞬間風向β(t)のデータを用いて
平均感度を計算した。
10分間の平均感度の72例の平均を求めると、σ=14.9°±1.9°(=0.260±0.033rad)
に対して理論的に計算された観測風速(熱線)=7.59m/s±1.93m/sであり、
実際の風速=7.83m/s±1.97m/s、したがって平均感度(=熱線/真値)=0.969±0.007で
ある。この平均感度が図57.7のσ=14.9°のところにプロットしてある。0.969+0.007
と0.969-0.007の値は同図の破線の縦幅で示した。
こんどは、瞬間風速 W(t)は同じ値として、瞬間風向のみ 0.5β(t)、1.5β(t)、2β(t)、
・・・3.5β(t)に変えて(つまりσを0.5倍、1.5倍、・・・・3.5倍)、同様に平均感度
を計算し、図57.7に○印でプロットした。同様に破線の縦幅が出力率の72例の標準偏差
である。
以上の計算から得られた熱線風速計の指向性から生じる誤差を表57.2にも示した。
また、表の最下列には平均風速の比較観測から見積もった結果も示した。
表57.2 熱線風速計(DT-8880)の指向性による誤差
誤差=[1-(熱線/真値)]×100(%表示)
方法・場所 風速(熱線) 風速(真値) 熱線/真値 誤差 観測時間
m/s m/s % 分×回数
理論(近似解析解)(1) ー ー 0.856 14 ー
理論(現実風向分布)(2)
σ=14.9° 7.59 7.83 0.969±0.007 3 10×72
σ=29.8° 6.94 7.83 0.884±0.025 12 10×72
σ=44.4° 6.20 7.83 0.790±0.039 21 10×72
水平2次元・事務棟跡(3) 0.57 0.70 0.83±0.14 17 10×9
(1)風向変動の標準偏差がσ=29.8°の正規分布の場合:「大気境界層の科学」の式3.54。
(2)10分間風向変動観測の72例の平均:農環研露場、2009年1月10日12時~24時、高度25mの
10秒ごとの実測値使用、σ=14.9°は実測値、29.8°と44.4°は設定値。
(3)真値は水平2次元超音波風速計による:自然教育園の旧事務棟跡の空地で観測。
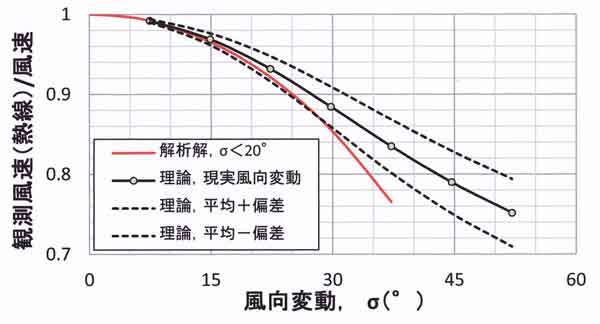
図57.7 熱線風速計の指向性による平均風速の平均感度 [=観測風速(熱線)/ 水平スカ
ラー平均風速の真値 ] と風向変動の標準偏差 σ の関係。
赤実線:風向変動が正規分布のときの近似解析解(「大気境界層の科学」、式3.54)
黒線と○印:現実の風向変動の頻度分布を用いた計算値(延べ12時間、72例平均)
破線:72例の平均値からの標準偏差の幅
参考1: 図57.7の黒実線をみると、風向変動が非常に大きくなると縦軸の値
(平均感度)は 0.7 程度に収束する傾向にある。熱線風速計を用いた実際の観測
では風向が大きく変化することに気づいたときは、センサーの向きを変えて測るので、
平均感度は0.7~0.8 以下には下がらないと考えてよい。つまり、体感・目視の風速値
と大きな違いは生じない。
参考2: 風向変動が極端に大きく、あらゆる方向から等しい頻度で風が吹くとき
の平均感度は、cosβ について β=0~π/2 までの積分の平均値 0.64(=2/π)に
等しくなる。
そのほかに、この安価な熱線風速計は気温が0℃近くの低いときや電池が消耗してくる
と、異常な風速を示すようになるので、気づいたときは電池交換をしなければならない。
つまり、器械に頼らず、絶えず体感でわかる実際の風向風速に注意していることで
ある。
農環研風速計の変更による風速比の補正
農環研露場の高度25m用の風向風速計は風車型(プロペラ型)であるが、高度8mと
1.85m用の風速計は2010年3月23日までは軽量小型の3杯式風速計(Met One 010C:
起動風速=0.22m/s)であったが、それ以後は25m用と同じプロペラ型
(YOUNG Model 05103:プロペラの起動風速=1.0m/s, 翼の回転起動風速=1.1m/s)
に変更された。
3杯式風速計は仰角特性をもつが、農環研の露場の高度1.85mにおける仰角変動の
標準偏差σ(θ)=4~10°の範囲にあると推定すれば(「大気境界層の科学」、
式3.57)、回転し過ぎの誤差は0.1~0.7%に過ぎず、無視できる(同書、図3.14:
ただし牧野応用測器社製軽量小型の3杯風速計の特性を用いた場合)。
前章で解析した資料は2009年のもので、2010年3月23日以前であるため、高度1.85mの
風速が高度25mに比べて相対的に大きめに観測されている可能性がある。
つまり、風速比(=U1.85/U25)が大きめに出ていると考え
られる。
毎日の日平均風速データから、U25>3m/s, かつ U1.85>2m/s
の条件を選び出して風速比を求めると次の値となった。
2009年・・・風速比=0.60±0.05
2011年・・・風速比=0.54±0.06
したがって、2009年が11%大きい。
表57.1に示した農環研の平均風速比は11%小さくなるので、露場通風率は90%から
81%に小さく補正した。
注6:表57.1に示した農環研の風速比は2009年の毎時データのうち
露場風速 U1.85≧3m/s の条件を満たす風速観測精度の高いデータの解析
による。
確かめるために、年間の毎日の日平均風速の全資料の平均値を用いて、風速と風速比の
経年変化を図57.8に示した。高度25mの年平均風速に大きな変化がないのに、
高度1.85の風速が2010年に不連続的に減少している。風速比のグラフ(右図)では
顕著に現れており、上記の補正でよいことがわかる。
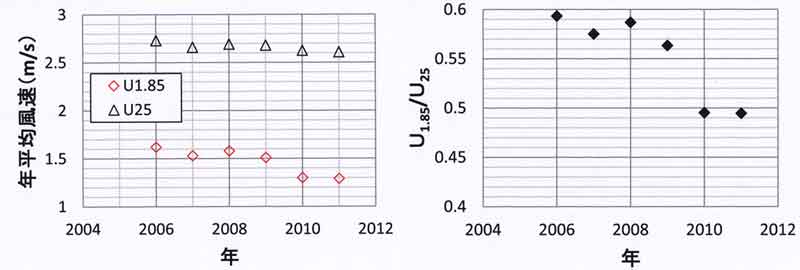
図57.8 農環研露場における風速(左)と風速比(右)の経年変化。
注7: 2010年3月23日に高度1.85m用の風速計を3杯式からプロペラ型に取り
替えて上下とも同じ器械とした。
したがって、それ以前の1.85mの風速が相対的に強めに観測されている。
注意として、右図に示す風速比は微風時(風速観測精度が悪い)も含むので、
この比は露場通風率の評価には用いない。
57.6 まとめ
熱線風速計による風速比・露場通風率は未補正:
熱線風速計の正しい指向性は、本章の観測の時点では不明であり、
いわゆる cos-law に近似的に従うものと仮定して「平均感度」を計算した。
その平均感度を参考にして風速観測値の補正を行い、風速比(=露場風速 / 測風塔風速)
や露場通風率(理想的な広い露場の風速を100%として表した露場の風速)と空間の
広さ=露場の広さとの関係を図に示す予定であった。
その後、2012年3月になって、次章「K58. 熱線風速計の検定と
指向性」において、正確な「平均感度」がわかった。熱線風速計のセンサーには
正方向と逆方向があり、両者による指示風速は10~35%も違うことがわかった。
当初、センサー部は肉眼で見る限り、正方向と逆方向が対象的に作られて
いるので、正方向と逆方向で指示風速は同じになると考え、その区別はせずに観測して
きた。例えば、センサー1と表示部 A の組み合わせで測ると、風速指示値 / 風速真値は
正方向で1.13、逆方向で0.84と大きく異なる。
多くは逆方向で観測し、途中で風向が大きく変るような場合は、センサーの向きを
正方向にして観測したりであった。そのため、風速は平均的
に弱めに観測されている。
さらに熱線風速計の指向性によって、狭い空間では風向変動が大きく、平均風速は
弱めに観測される。
いっぽう、表57.1の注1に説明したように、この章で示した空間の過半数は平塚市内の
公園で観測したもので、その基準となる測風塔風速は辻堂アメダスを用いてある。この
アメダスは防風林の近くの公園の駐車場にあり、測風塔高度が10mと低く風速が弱め
に観測されている可能性がある。そのため平塚で観測した
風速比は大き目に出ている可能性がある。
以上の理由により、本章の熱線風速計の補正は行わないまま
風速比と露場通風率をまとめることとした。
仮に補正したとしても、結果には概略±10%以内の狂いしか生じなく、全体的な傾向は
ほとんど変らないと見てよい。
本章のまとめ:
図57.9は開放空間の広さ(つまり露場の広さ)と風速比(=露場風速 / 測風塔風速)
の関係である。
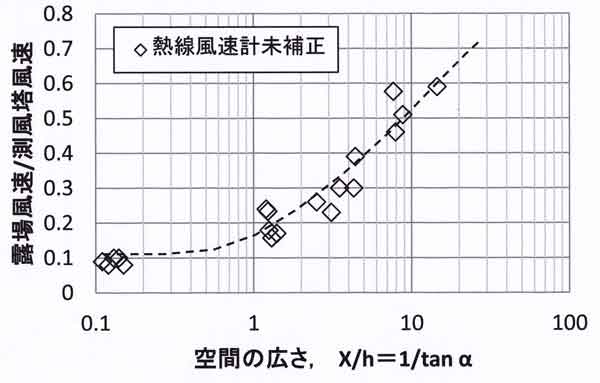
図57.9 開放空間の広さ(1/tanα= X/h) と風速比の関係、α:空間中心の
地表面から見あげた樹高の高度角、X:開放空間の半径、h:平均樹高、冬期(2011~
2012年)の観測による。風速比の各プロットの観測時間は延べ90分間(=10分間×
3回×3シリーズ)以上、農環研露場と筑波大圃場の値は2009年の1年間毎時観測に
よる。いずれも微風時のデータは含まない。
横軸は対数目盛りで表してある。理想的な露場の風速比は0.74±0.06であるので、
空間の広さ(無次元) X/h が40程度以上が理想の露場といえる。気候観測では、日だまり効果
による年平均気温が0.1℃以上の上昇であれば、問題となるので、現実には、空間の
広さは20程度あればよいのかもしれない。その気温上昇についての詳細は続報で述べる
予定である。
図57.10は露場通風率と空間の広さとの関係であり、前図と同様のことが言える。
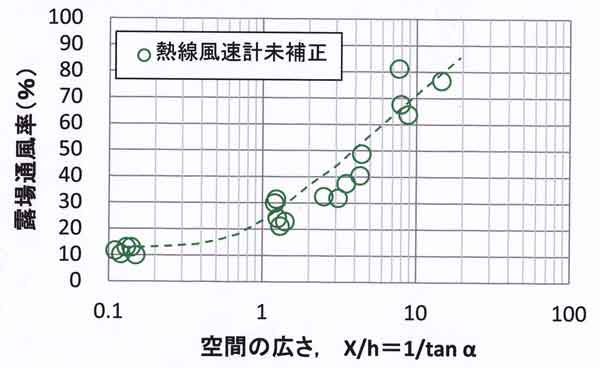
図57.10 図57.9に同じ、ただし縦軸は露場通風率(非常に広い理想的な露場の風速を
100%としたときの露場の風速)。
注意として、表57.1の注2にも記したように、露場通風率は、測風塔風速が近傍地物
の影響を大きく受けていないとき、測風塔風速に対して露場風速が大きく落ち込んで
いるかどうかを表すパラメータである。ところが現実には、測風塔の高度が不十分で
あったり、近傍の建物など(例:農環権研の南側にできた工場)の影響により、
測風塔風速が弱めに観測されていることもある。このような場合、風速比は大き目
に、同時に露場通風率が見かけ上大きな値となることがある(図57.10の横軸が7.7の
プロット=農環研のプロット)。
それゆえ、測風塔高度が低いときや、露場周辺に目立った建物・
樹木がある場合、通風率が大きいからといって、露場が理想に近いと判断しては
ならない。
次の計画:
このシリーズ研究は、気象観測所の露場周辺環境の維持保全の指針を作成することを
主な目的としてはじめたものである。
「日だまり効果」によって平均気温がいかほど上昇するかの具体的見積もりと実測を
行う前に、現実の気象観測所数か所について、本章と同様に開放空間(露場付近)の
広さと風速比の観測を行う。それら現実的な資料を参考資料にして、日だまり効果に
よる平均気温の上昇量を具体的に見積もりたいと考えている。
参考文献
Hayashi, Y., 1983: Aerodynamical properties of an air layer affected by
vegetation. Envi. Res. Center (ERC) Papers, Univ. of Tsukuba, No.3, 1-51.
Kondo, J. and G. Naito, 1972: Disrurbed wind fields around the obstacle
in sheared flow near the ground suraface. J. Meteor. Soc. Jpn., 50,
346-354.
近藤純正、1982:大気境界層の科学.東京堂出版、pp.219.
近藤純正(編著)、1994:水環境の気象学ー地表面の水収支・熱収支ー.朝倉書店、
pp.359.
資料
石郷岡康史・桑形恒男・横沢正幸・後藤慎吉・宮田 明、2006:新しい農業環境技術
研究所総合気象観測資料,インベントリー、第5号、20-22.
農業環境技術研究所:公開気象観測データ.1990~2012(継続中).http://niasaws.
ac.affre.go.jp/
渡来 靖・藪崎志穂・山中 勤、2006:熱収支・水収支観測データベース図表集、
1981年8月~2005年12月.筑波大学陸域環境研究センター報告、第7号別冊、pp.97.
渡来 靖・山中 勤、2007:熱収支・水収支観測資料ー2006年ー.筑波大学陸域環境
研究センター報告、No.8、55-80.
大庭雅道・山中 勤、2008:熱収支・水収支観測資料ー2007年ー.筑波大学陸域環境
研究センター報告、No.9、49-74.
大庭雅道・濱田洋平・山中 勤、2009:熱収支・水収支観測資料ー2008年ー.筑波大学陸域環境
研究センター報告、No.10、83-108.
鈴木智恵子・池上 翔・山中 勤、2010:熱収支・水収支観測資料ー2008年ー.筑波大学陸域環境
研究センター報告、No.11、35-60.
鈴木智恵子・池上 翔・山中 勤、2011:熱収支・水収支観測資料ー2008年ー.筑波大学陸域環境
研究センター報告、No.12、xx-xx.









