
このようにリンクの先端、あるいは一部分が直線運動をする機構を 直動機構といい、機構学の本に代表的な物が掲載されています。 しかし既存の直動機構は複雑すぎて「らぴすらずり」に搭載する事ができません。 そこで僕は4節リンクに注目しました。 これは文字どおり4本のリンク棒からなる最も簡単な機構で、 各リンク棒の長さを変更する事で さまざまな軌跡をリンク先端に描かせる事ができます (かわさきロボットの足として多用されるチェビシェフ近似直動機構も4節リンクの一種です)。
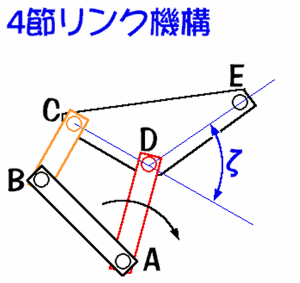
各リンク棒は接続されていて軸を中心に回転する事ができるようになっています。
ここでリンクDAが点Aを中心に回転したときに点Eはある動きをしますが、 この動きを使ってICBEを相手マシンの所まで運搬しようというのが僕の着想でした。
それは調べなければならないリンクの種類が多すぎるという事です。
図1において、固定されているリンクABの長さを1とし、
角度ζは一定として、BC,CD,DA,DEについてのみそれぞれ10通りの長さを調べるとしても、
調べる4節リンク機構の種類は10×10×10×10=10000通りとなります。
工作用紙を使うなどしてリンク機構の模型を作り、
リンク棒の動作を確かめていたら、時間ばかりかかってしまう事は明らかでした。
そこで各リンク棒の長さを与えると、 リンク機構がどのような動きをするかを計算するMatlabスクリプト −プログラムをまず作る事としました。
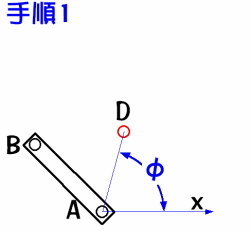
点A、点Bは固定点ですから位置を求める必要はありません。 全ての計算はここからスタートする事になります。
次に点Dの位置を決定します。 これは∠DAx=Φとすれば(DA×cosΦ、DA×sinΦ)として求められます。
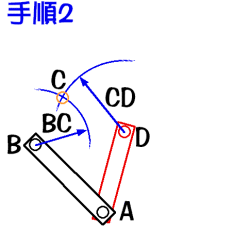
実際の計算では円の連立方程式を使う方法と、 ロボットアームの解析の初歩の練習問題としてよく使われる 2自由度SCALA型ロボットアームの逆運動学の問題として解く方法の二つがあります。 ogulinkでは後者を採用しています。
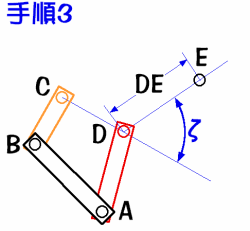
これはある角度Φに対する点Eですから、 Φに別の角度を入れて点Eを求める事を繰り返します。 するとΦの変化−−つまり点Aを中心としたリンクDAの回転に応じた 点Eの軌跡が得られるわけです。
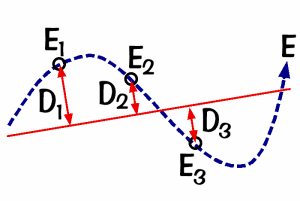
まず点Eの軌跡(左図の太い青の鎖線)から、 回帰計算によって直線(赤線)を導き出します。 次にこの直線とそれぞれの点E(E1、E2、E3……)との距離を調べます。 そして得られた距離を全て合計します(D1+D2+D3+…)。
この方式でまず1万通りのリンク機構に順番をつけた後、 上位の結果を得たリンク機構を選び、 改めて点Eの軌跡を調べて僕が最終的決定を下しました。
こうして決定されたリンク機構がどのような動作をするかは、 「らぴすらずり」のページを参照してください。
むしろogulink開発の意義は、 こういうスクリプトを作るのは非常に簡単である事を示した点にあります。 ささやかな計算機とちょっとしたプログラミング能力さえあれば 工作用紙と画鋲と方眼紙をリンク設計の過程から取り去り、 はるかに速いテンポで独自のリンク軌跡の検討が行えるのです。 さらにogulinkは中上君製作の 多節リンク汎用解析システム「LCL」 の開発の契機となるという役割を果たしました。 単品生産のためのスクリプトとしては、 まずまずの役割を演ずる事ができたといえるのではないでしょうか。