

この「ヘッケン+VMCの組み合わせ」は既に1997年第4回の ボウラ甲型 に始まりを見ることができます。
しかしVMCの導出については 近似的に円とみなしてCADなどでトライアル&エラーを繰り返す という手法が主流であり、詳しく解析的に追求した結果は 少なくともインターネット上では公開されていないのが実情です。
そこでラグオ電工異常設計事業部ではVMCの導出を 「らぴすらずりIX」 で採用した脚を例にとって解説し、 あわせて汎用のVMC導出プログラムを公表する事でかわさき参加者が 手軽にVMCを作成できるようにする事としました。
なお、CADを使った導出の仕方は 「機械の館」 さんが詳しく紹介しています。
さらに欲をだして、 通常は120°対向3枚で構成されるVMC用脚機構を180°対向2枚で構成する事をもくろみ スクリプトrectiflegを作成してVMCを計算で求めました。 しかし周囲の大会参加者の大半は VMCを円と近似してCADで円の半径を計算しているようでした。
正確なところ、足先の形状は円なのか否か、 VMCに使用するリンク機構としてはもっとも単純な「らぴすらずりIX」 「らぴすらずりIXx」の脚機構を対象として計算で結論を求めてみようと思います。

図1:らぴすらずりIX/IXxのVMC
らぴすらずりIXで使用したVMCの概念図を図2に示します。 スロッテッドクランクを元にVMCを構成しています。
ここで、
| A: | 原動節の軸の位置ベクトル(0,h) |
| B: | スロットを固定するピンの位置の位置ベクトル(0,H) |
| φ: | 原動節の角度(0〜2π) |
| D: | 原動節の先端の位置ベクトル(cosφ,h+sinφ) |
| F: | 補正曲線 |
| F0(φ): | 補正曲線の接地点 |
| l: | BD軸上の長さ1のベクトル |
と記号を定義します。なお原動節は一般性を失うことなく長さ1とおく事ができます。
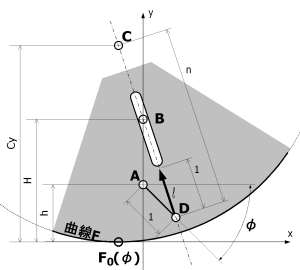
図2:らぴすらずりIXの脚機構概念図
ここで 曲線Fを円と仮定します。すると中心Cのy座標はφが変動しても一定です。
また円の中心Cと原動節の先端DはリンクBDを含む足先板(灰色部分)に固定されていますから、 CDの距離も一定となります。 そこで円の中心Cの座標をC=(Cx,Cy)とおくと、 点DからB方向に伸ばした単位ベクトル lに対してφに依存しない定数nが存在して以下の条件式が成り立ちます。
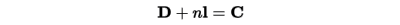
ここでそれぞれに値を代入し、 問題となるy軸側の値(Cy)だけを取り出すと、以下のようになります。
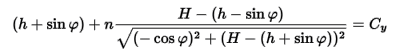
ここで調べたいのはCyがφによらずに一定値となるかどうかなので、 上の式をφで微分してみます。すると結果は以下のようになります (左辺と右辺がひっくり返っています。ご注意ください)。
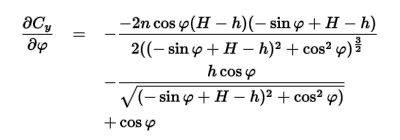
ここでnを適切な固定値にすると右辺の式がぴったり0になるとすれば、 そのnに対して曲線Fは円となる条件を満たしている事になります。 一方、どの値を選んでも右辺の式が0にならないならば、 曲線Fは円でないという事になります。
そこで上の式を=0としてnで解きます。すると、
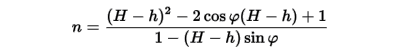
となります。解けはしましたが、nがφに依存している事が分かります。
唯一の例外はH=hの時で、この時n=1となります。 しかしそれは支点Bと原動節の軸Aが一致しているという意味ですから、 そこから得られるのは車輪のような脚どころか車輪そのものです。
というわけで、車輪そのものを除くVMCでは、CDの距離をφの変化にあわせて変えてやらないと、 dCy/dφ=0を満たすことはできません。 曲線Fが円であるとすればnはφに依存しない一定値となるはずなので、 以上の結果は曲線Fは円ではないという事を示しています。
今回はスロッテッドリンクを利用したVMCについて、 それは円ではないということを証明しました。 ヘッケンリンクを利用したVMCについては計算をしていませんが、 状況はほぼ同じと考えています。誰か計算して確証を得ませんか。
曲線Fは任意の原動節角度φに対して、y<0の領域に入り込む事はありませんし (あったら足先が地面にめり込む事になります)、 脚が歩脚である間はx軸から離れてしまう事もありません (それじゃマシンが飛んでいる事になります)。
また、曲線Fはそのどの場所をとっても下に凸のカーブを持っています (仮に凹の部分があったとすると、 その部分は地面に触れないのでVMCとしては役に立っておらず、 曲線Fから除外する事ができます)。
というわけで、図2に示したF0はあるφに対して1点と仮定できます。 そこであらゆるφに対するF0(φ)の位置を次々求めていき、 それをつなげば曲線Fが作れそうです。
| F0(φ): | 補正曲線の接地点 |
| B(φ): | 中間節BDの支点 |
| P(φ): | Dを通りBDに直交する線がx軸と交わる点 |
| S(φ): | BDの延長線がx軸と交わる点 |
| Lp: | DP(φ)の距離 |
| Ls: | DS(φ)の距離 |
| XY軸 | リンクBDに固定された座標(大文字注意) |
今回は支点Bがφに依存して移動すると定義されていることに注意してください。 通常の四節リンク機構では、中間節の位置は原動節の角度に応じて移動するからです。
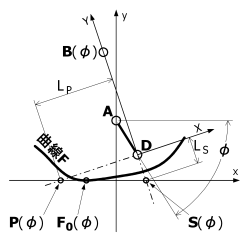
図3:VMC導出用の変数定義
「BDの延長線」と「Dを通ってBDに直行する直線」が それぞれx軸と交わる点がS(φ)、P(φ)です。 それぞれの直線の方程式は
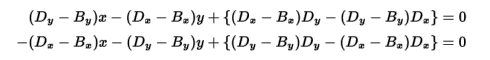
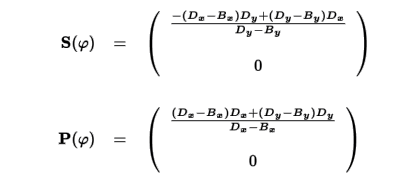
となります。DxとかByとか気安く書いてありますが、全部φの関数であることをお忘れ無く。
さて、曲線FはリンクBDにくっついて動くものなので、 この先は地面と胴体を基準としたxy(小文字)座標軸を離れて、 Dを原点とし、リンクBDに固定されたXY座標軸(大文字)に移ります。
xy座標からXY座標への回転変換行列E(-ζ)を作るためには、 当然の事ながら回転角ζを求めてやる必要がありますが、 今までそんな変数一言も触れてこなかったように、 全くノーマークだったわけです。
今更arctanとかを使うのも何だか無理矢理な感じがしますが、 実は既存の変数だけで回転変換行列E(ζ)を作ることができます。
右の図4が回転角ζと支点B,Dの関係です。
この関係を基に回転変換行列を書きます。すると以下のようになります。
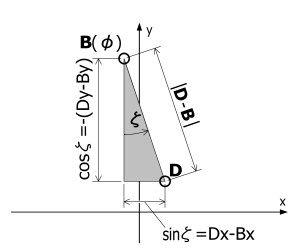
図4:回転角ζと支点B,Dの関係
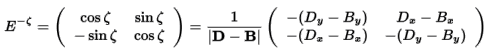
さて、この回転変換行列と平行移動を使って、S,PをXY座標で表しなおしてみましょう。
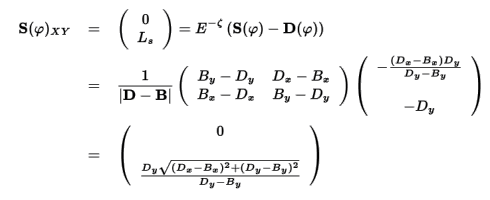
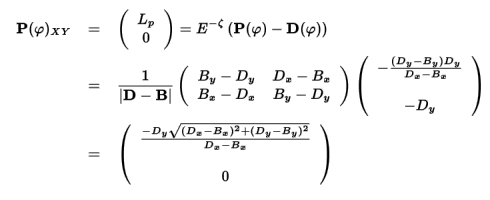
となります。何だかやたらに面倒になってきましたので、 ここから先はLs(φ),Lp(φ)で記述を進める事にします。 中身についてはこういう式なんだということをとりあえず覚えておいてください。 後になっても出てきませんけど。
さて、XY座標軸の下ではもとのx軸(地面)はSXY,PXYを通る直線として表せ、 以下のような式になります。
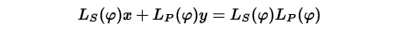
この直線を図5のようにφ=φ,φ=φ+Δ,φ=φ-Δと、φを変えて3本求めた時を考えます。 この時、F0(φ)は前提条件からP(φ)とS(φ)を結ぶ線上にあります。
よって、F0(φ)が存在できる場所は図4で青い太線で示した部分だけになります。
この青太線で示した部分の始まりと終わりは、それぞれS(φ),P(φ)を通る直線と、 S(φ±Δ),P(φ±Δ)を通る直線の連立方程式の解として求めることができます。
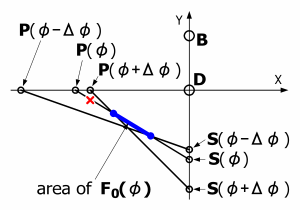
図5:S(φ)とP(φ)とF0(φ)の存在位置
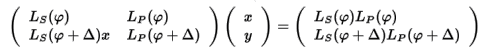
となり、その解は
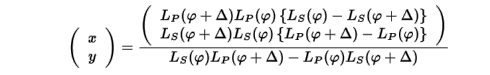
となります。行列で書いてあるからすごそうですが、 その内実は単なる2元1次の連立方程式です。
ここでΔ→0とすれば図4での青線の範囲がどんどん狭まっていき、ついには一点となります。 これが求めようとしていたF0(φ)の位置です。 この手順をVMCを必要とするすべての角度φに対して実行すれば、 必要な曲線Fを求めることができるのです。 もっともコンピュータにでも実行させなかったらとても面倒ですから、 これをそのまま手作業で実行することはおすすめしません。
F=VMCGen(B,D)
とタイプすることで実行されます。与える引数と返値は以下の通りです。
| B: | 図3の支点Bの座標。 今までの導出の中では固定値でしたが、VMCGenではn行2列の入力を許します。 これはヘッケンリンクを使用した場合などで支点Bが揺動運動した場合でも VMCを求められるようにするためです。 |
| D: | 図3の原動節の先端Dの座標をn行2列で入力します。 |
| F: |
VMC曲線FをXY座標で返します。(n-1)行2列の列ベクトルになります。
なお、このVMC曲線の原点(0,0)はクランクの先端Dとなり、Y軸はリンクBDと一致します。 |
これらB,Dでnの値は一致している必要がありますが、
FはVMCGenによって勝手に生成されるので心配の必要はありません。
また、エラーチェックは一つもしていないので、
B,Dの値につじつまがあっていなくても怪しげな曲線Fが生成されますが、
当然それは使えません。
次にらぴすらずりIXの脚機構のパラメータを入力します。値は以下の通り。 記号は一番最初の図2で定義した物と同じです。 ただし今回は原動節ADの長さで正規化していないのでADの長さも入れる必要があります。
| h: | 36[mm] |
| H: | 63[mm] |
| ad: | 18[mm] |
図6:octaveの起動
h=36;
H=63;
ad=18;
phi=linspace(pi,2*pi,100)';
B=[zeros(100,1) ones(100,1)].*H;
D=[ad*cos(phi) h+ad*sin(phi)];
で、最後に
F=VMCGen(B,D);
と入力するとFにVMCの結果が入ります。
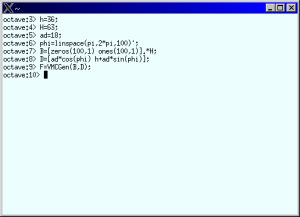
図7:パラメータの設定とVMCGenの実行
hold on; axis('equal');
plot(F(:,1),F(:,2),";curve-F;");
plot(B(:,1),B(:,2),"@16;joint-B;");
plot(D(:,1),D(:,2),";joint-D;");
別のウィンドウが開いて、右図のような結果が得られるはずです。 赤い線が今まで求めてきたVMCを与える曲線Fです。 試行錯誤は全くなし。簡単ですね。
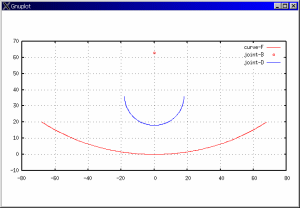
図8:結果の表示
| AD | 55[mm] |
| OB | 165[mm] |
| BD | 80[mm] |
| DE | 80[mm] |
| AO | 150[mm] |
さて通常の四節リンクの場合、 当然の事ながら支点Bは固定でなく揺動するのでこの揺動運動を求めてやらなければなりません。
そこで、やはりMatlabのスクリプトを用いて脚機構の動きを求めつつ、ついでにグラフ化してみました。 すると図9のようになります。
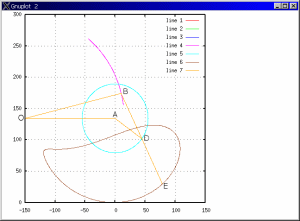
図9:ある四節リンクの動き
ここで実際にVMCを求める際に必要なのは、BとDの動きだけです。
これは、角ζが最大・最小の付近でVMCを追求するのは現実的ではない と言うことを示しています。
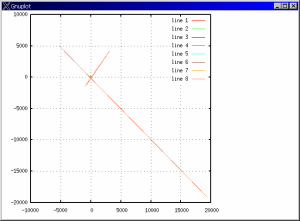
図10:発散した解
またその前後のかなり広い範囲で曲線Fは非現実的な値となるので、 暫定的にφ=200〜360°で計算をしてみました。 結果は図11のようになります。 オレンジ色の線がVMCを与える曲線Fで、 その内側の赤色の線が足先を円と近似した場合の曲線になります。
グラフより、二つの曲線が似たカーブを描くのは中央の一部のみで、 周囲に行くに従い次第に乖離していくことが分かります。
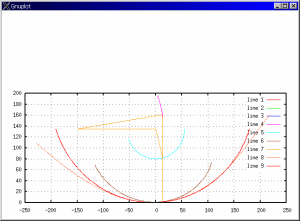
図11:原動節角度を限定した解
VMCGenを利用することで、近似では得られない厳密な上下方向移動零化足先を容易に構築することができます。 これにより設計者はVMCをいかに設計するかという入り口での問題に時間を取ることなく、 よりよいVMCの追求という一歩先の問題に十分な時間をかけることが可能となります。
またVMCGenが生成する曲線Fのデータを解析することによって、 VMCを利用した場合のマシン速度、 あるいは地形対応能力といった新たな見地での足先の設計も可能となることでしょう (マシン速度についての議論はラグオ電工でも後ほど展開する予定です)。

詳しくはアーカイブ同梱のLISENCE.TXTを見てください(LICENCE-ja.TXTの日本語訳は参考です)。 ライセンスを解釈する場合、LISENCE.TXTの内容が唯一正式なものになります。