2021.05.24
      気になったので、ウイルス増殖を記述する Viral Kinetic Model について幾つか論文を読んでみた。
●COVID-19でのウイルス量と死亡率の関係について
Modeling SARS-CoV-2 viral kinetics and association with mortality in hospitalized patients from the French COVID cohort
N. Neant et al.
PNAS 2021 Vol. 118 No. 8 e2017962118
・・・・・・・・・・・・・・・・・・・・・・
      2020年4月までの入院者の死亡リスクにウイルス排出量が関係していることを明らかにした。高齢、男性、心臓疾患というリスク因子とは独立にウイルス排出量という死亡リスク因子があることが判った。ウイルス排出量について、モデルを作った。Marc et al. がそのモデルを使って、ウイルス排出量を二次感染確率の相関性を証明したのだが、Marc の使ったのは、免疫効果を除いたものである。モデル自身についてもこちらの方がやや詳しいので、そちらに焦点を合わせて読んだ。論文の主旨とはやや外れているので、興味のある人は原文をお読みください。
・・・・・・・・・・・・・・・・・
初期条件や基本的なパラメータは同じである。患者のデータは発症日基準であるが、潜伏期間を５日に固定することで、感染日を推定している。
その感染日からウイルス排出モデル、Viral Kinetic Model がスタートする。可変パラメータは、ウイルスの感染力 β、感染細胞の死亡率 δ、ウイルス産生率 p である。これらのパラメータをまとめて Ψ とするが、これによってウイルス排出量の経時変化 V(t) が決まる。（下式 V＝Vi＋Vni）

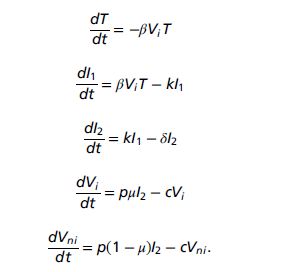
パラメータは個人個人によって異なり、その平均値と分散を持つから、これら６つのパラメータで決まる対数正規確率分布に従う。
個人を i、PCR検査を j で表現し、その検査日を感染日から tij とすると、ウイルス排出用 Vij は、３つのパラメータ（まとめて Ψi）で既定された時刻 tij での計算値となるが、これは勿論実測値  Vij(obs) とは異なる。その差が正規分布に従う確率変数であるとして、εij とすると、
・・
   Vij(obs)＝V(Ψi,tij)＋εij、 Ψi＝γ×exp(ηi)
ということになる。確率変数 ηi は正規分布である。
・・
Ψi と εij が分布を持つが、その分布の最大値が  Vij(obs) となるような γ と ηi を決めればよい。
Stochastic Approximation Expectation Maximization （SAEM）法というのがあるらしい。後述する。
EM の部分は Back Projectionで知っている。決めるべきパラメータから決定論的に決まる中間的なパラメータを固定しておいて、その上で決めるべきパラメータを最尤推定する。こうして得られたパラメータを使って、元に戻る。この繰り返しであった。
Back Projection では、感染発生確率を決めるパラメータ λ(t) から、潜伏期間分布 ρ を使って、中間的なパラメータ ρ(Δt)λ(t) が決まるので、これを観察された発症者数 y(t)obs から比率計算で仮に決めてしまう。そうすると、尤度最大となるような λ(t) が簡単に決まる。ポワッソン分布なので、簡単であったが、今回のはややこしい。
別途、R に導入した人の書いた説明論文を読んだ。⇒ 一番下に記述（E. Comets et al.）

・・・・・・
      結果は下記表にまとめてある。高齢、男性、心臓疾患というリスク因子とは独立にウイルス排出量という死亡リスク因子があることが判る。

・・・・・・・・
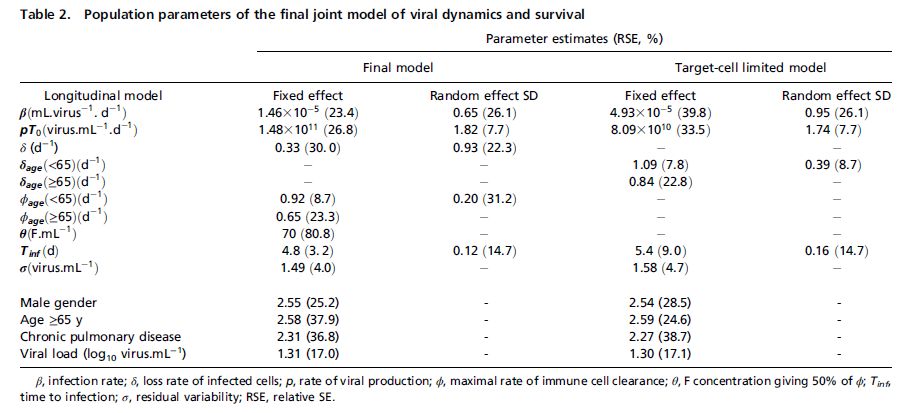
免疫効果については、因子 F を考えて、Ｆの時間変化 dF/dt がウイルス生産性細胞数 I2 に比例して増加し、F に比例して減少する。
・・
   dF/dt＝I2 - df×F
平均寿命が 1/df となる。
この免疫因子 F が具体的にどう作用するかであるが、ざっくりと、I2 を減らす効果として
・・
  - Φ(F/(F+θ))I2
を入れている。
付属資料の中では、他の免疫効果メカニズムも考えて試しているようである。

・・・・・・・・・・・・・・・・・・
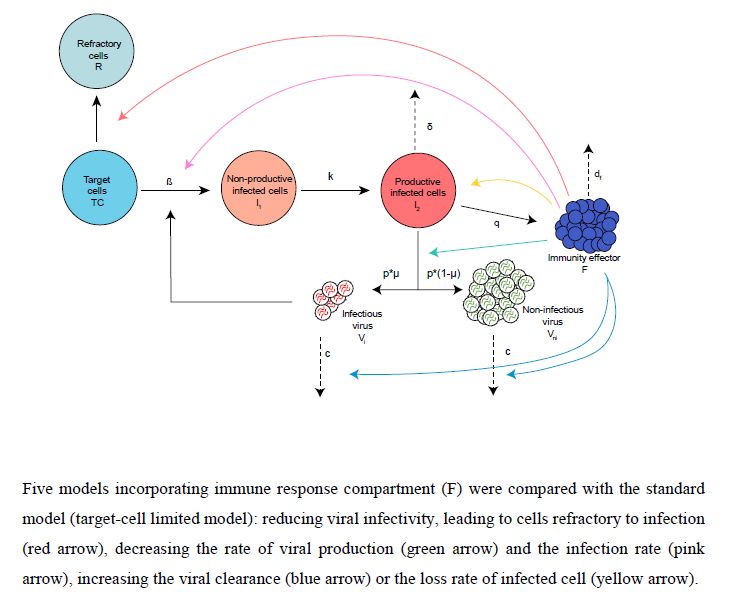
●COVID-19での早期治療の重要性について
Timing of Antiviral Treatment Initiation is Critical to Reduce SARS-CoV-2 Viral Load
Antonio Goncalves et al.
CPT Pharmacometrics Syst. Pharmacol. (2020) 9, 509?514; doi:10.1002/psp4.12543
・・・・・・・・・・・
Viral Kinetic Model としては、多分 Neant より前である。感染によってウイルス量が減る効果 －βTV が入っている。もう一つは、発生するウイルスが全て感染に寄与するようになっている。Neant では発生ウイルス量の 10000分の1 しか感染に寄与しない。これでデータフィッティングする、ということは βが 10000分の1 になる、ということで、実質的には同じことである。感染細胞が何個の感染細胞を生み出すか、という基本再生産数は
・・
  R0＝pβT0/δ(c+βT0)
・・
で、分母の違いがウイルスが感染によって消費される効果である。
Neant の場合は、
・・
R0＝pβT0μ/δc である。μ＝1/10000 である。
・・
パラメータ分布の推定は同じく SAEM で行っている。
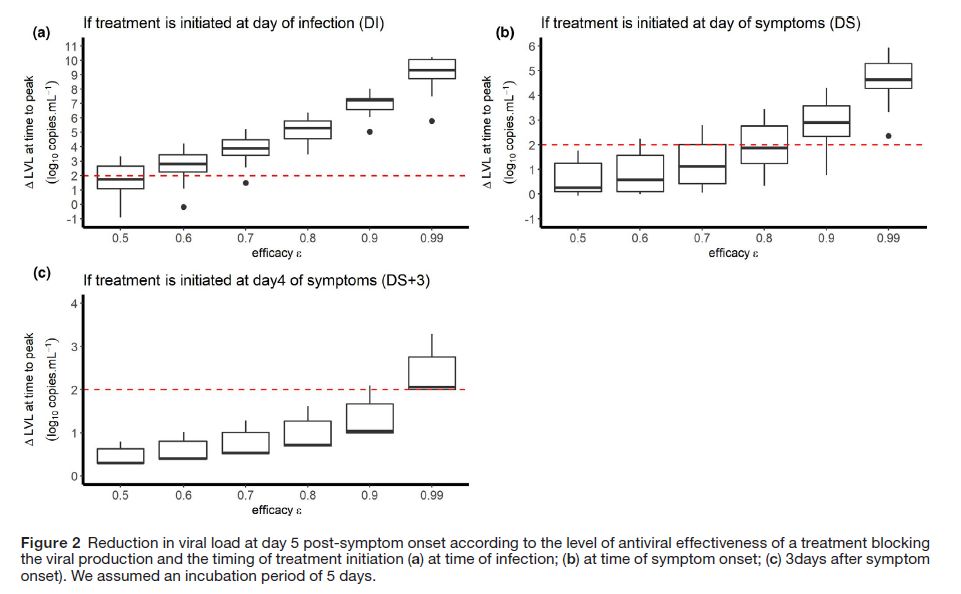
研究の目的は、治療介入の時期と効果である。
早く治療することで重症化が防げるというのが結論である。
治療効果をモデルのパラメータ R0 の変化として取り入れている。その具体的な推定方法については医学的知識が必要であるので、僕は読んでいない。
下図は横軸に治療の強度、縦軸にウイルス排出量低減度合いがプロットされている。各図が治療開始時期の違いである。

・・・・・・・・・・・・・・・・
●感染細胞に待機期間（V1）を入れたのと、V1による自然免疫誘導（IFN）効果の検証
Kinetics of Influenza A Virus Infection in Humans
Prasith Baccam et al.
JOURNAL OF VIROLOGY, Aug. 2006, p. 7590?7599 Vol. 80, No. 15
・・・・・・・・・・・・・・・
序文を読むと、体内でのウイルス増殖の数学的モデルは、1990年代以降、治療効果を表現する為のモデルとして様々に試みられてきた。感染の進行が極端に遅い HIV ウイルス感染については特にモデル構築が容易であるために、重要な役割を果たして来たが、進行の速いインフルエンザのような感染症ではなかなか難しい。
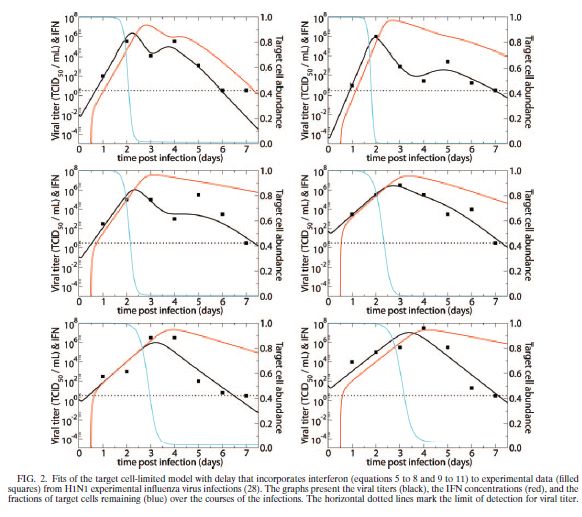
これは2006年の論文で、対象は H1N1 A香港型インフルエンザ である。HIVでのモデルを参考にして、必要最小限まで単純化してある。ただし、感染してもまだウイルスを出さない時期（V1）を入れない場合と入れた場合を両方やっていて、入れた方が良く合うことを示している。従って、SEIRモデルとほぼ同じモデルになる。パラメータは直接的に個別の感染者に対して最小自乗法で求めている。この場合は発症が早いので、ウイルス量最大値よりも前のデータが得られているところがCOVID-19とは異なり、パラメータ決定に有利であったと思われる。半分くらいの感染者ではウイルス発生量が２つのピークを持っており、これは感染された細胞が IFN を出して感染を抑制しているという効果を方程式に追加することで説明できる。感染してから少し遅れて IFN （赤線）が出始めて感染を抑制する。なお、COVID-19ではこの IFN の発現が抑制されるために、自然免疫が抑制され、発症も遅れ、感染の発見も遅れる。

・・・・・・・・・・・・・・・・・・・・・・・
●非線形混合モデルの解法：SAEM
Parameter Estimation in Nonlinear Mixed Effect Models Using saemix, an R Implementation of the SAEM Algorithm
E.Comets et al.
Journal of Statistical Software August 2017, Volume 80, Issue 3. doi: 10.18637/jss.v080.i03
・・・・・・・・
２．1.  非線形混合効果モデル
・・・・・・・・
  個人 i と その個人についての測定を j で区別する。測定時刻は xij である。測定結果は yij。測定値 yij についての非線形モデルがあるとする。そのパラメータを Ψi とする。つまり、Ψi が決まれば、yij は非線形関数 f(Ψi,xij) で予測できる。
Viral Kinetic Model であれば、f() はウイルス量の対数であり、Ψi は、ウイルス感染率 β、感染細胞死亡率 δ、ウイルス算出率 p、ウイルス死亡率 c、、、等々である。これらは、個人 i に依存するが、一旦パラメータが決まれば、あとは決定論的に yij が決まる。しかし、実際の測定値はそれとは異なるので、その差を誤差項として考える。測定誤差は勿論あるし、そもそもモデル自身の不確実性もその中に含まれている。
・・
  yij＝f(Ψi,xij) + g(Ψi,σ,xij)εij
εij が正規分布に従うように g が選択される。
・・
個々の i に対して j が沢山あれば、それぞれの Ψi を最適に決めることができるだろう。そして、Ψi の推定誤差も得られるだろう。2007年の Baccam 論文では H1N1 A香港型の解析を最小自乗法で行っている。しかし、COVID-19では、実際問題として j の数が多くないのが普通である。
そうすると、全ての i についての測定値 yij を使って推定誤差を小さくすることが考えられるが、全ての人が同じパラメータを持っているという仮定の元で異なる i のデータを足し合わせてしまうわけにはいかない。
これは、メタアナリシスと同じ状況である。つまり、個人差があるために、Ψi についてのバラツキを考慮しなくてはならない。
このバラツキの程度、つまり分布関数は正規分布であることが望ましいが、必ずしもそうではないので、正規分布に従う別のパラメータ φi を考えて、Φi から Ψi には適当な変換を考えておく。
・・
  φi＝h(Ψi)； Ψi＝h^-1 (Φi)
・・
Ψi の分布の期待値を μ とする。これは全ての人 i についての平均である。
Ψi の期待値から Φi の期待値へは線形変換 Ci で変換され、Φi がその周辺での正規分布をする。
・・
  φi＝Ci μ + ηi
・・
と書ける。ηi は個人毎に異なり、これを確率変数として扱う。
h の関数形は状況に応じていくつか選べる。単なる定数であれば、Ψi が正規分布という仮定になる。対数であれば、対数正規分布という仮定になる。他、logit や probit も選択可能である。これは解析における基本的な仮定であるから、経験的に選択される。
g については、通常定数としてしまうが、ウイルス量が多い程誤差も多いと考えて、f に比例するという選択もある。
結局、Ψi を個人誤差の分布として捉えていて、その分布関数は変数変換すれば正規分布となるように設定されていて、その正規分布を定義するパラメータが、Ci μ, vec(Ω),σ ということになる。
・・ μ はパラメータ Ψi の期待値であり、固定効果という。
・・ Ω は正規分布の共分散行列である。ランダム効果という。
・・ σ はこれらの分布とは独立した誤差分布の標準偏差である。
・・・・・・・・
２．２．パラメータ推定
・・・・・・・・
      パラメータ推定は最尤法を使う。尤度は個々の i の尤度の積になる。それは、観測値 yij を与えるような パラメータ θ での確率分布値であるから、p(yi|θ) と書く。パラメータ θ によって、ηi の「分布」が決まるのだから、yij を与えるような ηi について、θ で決まる元の確率分布を積算すればよい。
ここで、yi＝(yi1,yi2,yi3,,,) と表記する。
・・
  p(yi|θ)＝∫p(yi|ηi,θ)p(ηi|θ)dηi
・・
である。
ここで、p(yi|ηi,θ) は、θ と ηi が決まった条件下で、yi となる確率である。
そもそも yi の計算値 f は、 θ という確率分布において、パラメータ μ と 確率変数 ηi が決まれば Ψi が決まり、確定するが、
実測値とは一般に異なり、その差分を埋めるものとして、誤差項 εij があるので、p(yi|ηi,θ) とはその確率分布のことである。誤差項の標準偏差 σ は θ に含まれているので、これは計算できる。
対数尤度の全体は i についての和となり、
・・
  logL＝∑i log(p(yi|θ))＝∑i log(∫p(yi|ηi,θ)p(ηi|θ)dηi)
・・
である。
これを最大化するような θ を直接計算するのは困難であるから、２段階に分けて繰り返し計算をする。
・・
（１）Expectation
      この対数尤度に対して、k 回目の試行解 θ(k) での期待値を考える。そのために、個別の パラメータ Ψi の期待値を考える。
何も条件が無ければ、Ψi の期待値は Ψi＝h^-1 (Φi) の期待値であるから、μ となるが、
yij という個人差と測定誤差を含む測定値による拘束条件が加わるために、ηi の確率分布が条件付きになる。
つまり、ηi を動かして Ψi を変える。 それだけでは足りないので εij も動かして、yij が再現されるような ηi、εij を選ぶことができて、その範囲で Ψi の期待値を計算する。その全体の確率は θ(k) の一部として、 Ω と σ で決まっているから、これに拘束条件をいれて、その確率で Ψi の期待値を計算する。実際には MCMCで計算するようである。
・・この Ψi の期待値というのが、BackProjection における一次感染者数（ポワッソン分布のパラメータ λ(t)）による Δt 後の発症確率 y(t+Δt) への寄与 λ(t)ρ(Δt) に相当する。ρ() は潜伏期間分布である。BackProjection の場合は、実測値 y(t) を比例分割して、λ(t)ρ(Δt) を求めているが、ここではそこに確率計算が入る。
・・
（２）Maximization
      Ψi の期待値が決まると、それを実現するような θ についての尤度が決まる。
Ψi の分布は パラメータ θ で決まる単純な多次元正規分布の exponent であるから、最大尤度となる θ が決まる。
つまり、仮定した θ＝θk が新たに更新される。
この繰り返しである。
・・
最終的には、分布パラメータ、μ、Ω、σ が得られ、Ψi も期待値として決まる。
・・・・・・
２．３．対数尤度の推定
・・・・・・
２．４．標準誤差の推定
・・・・・・
    決定されたパラメータ θ＝(μ, Ω, σ) に対する標準誤差であり、これは尤度関数最大点付近での先鋭度である。
・・・・・・
２．５．モデル評価
・・・・・・
    使われたモデル f() が適切であるかどうかの指標。
・・
３．ソフトウェア
・・・
    既に Monolix というソフト（Lavielle 2014）が流通していて、使われている。MATLAB にも導入された。
    R としては、2017年 saemix という library を作った。saemixModel() でモデルオブジェクトを作り、saemixData() で解析データオブジェクトを作り、saemix() で解析を実行する。
・・・・・・・・・・・・・・
●計算原理のまとめ
・・・・・・・・・・・・・・
    判りにくいので、再度言語化してみた。

パラメータ Ψ が個人個人の差異による分布を持つ。Ψ が決まればウイルス量 V の経時変化が計算できる。だから、実測されているウイルス量から Ψ を個人別に最適決定することは出来る。その時計算されたウイルス量と実測されたウイルス量との間の誤差（εij）があり、それを最小化すればよい。しかし、実測データは限られているから、Ψ の予測誤差は大きくなる。多人数のデータを統合して Ψ のより良い予測値を求めたいが、個人間にパラメータ Ψ のバラツキがあるので、単にデータ数を増やすだけでは意味が無い。メタアナリシスと同じ状況である。メタアナリシスと同じように、個人間のバラツキをモデルに取り入れた上で、Ψ の個人間バラツキ Ω と全体としての期待値 μ を推定するのが、混合モデルである。バラツキ Ω のことを変量効果（ランダム効果）、Ψ の全体としての期待値 μ を固定効果と呼ぶ。

・・・基本的な原理は最尤法である。Ψ の分布パラメータ（固定効果 μ と変量効果 Ω）とウイルス量予測の誤差（εij）分布パラメータ（正規分布の標準偏差 σ ）の全体が分布パラメータ（θ＝(μ, Ω, σ)）である。観測されているウイルス量 Vij が実現するような全ての確率変数 の値の組（Ψi と εij）だけの空間（D）を考えて、その空間で分布確率を積分計算すれば、それはパラメータ θ の元での、Vij という拘束条件での尤度（L(Vij|θ)）である。これを最大化するように θ を決めればよいのだが、容易ではない。

・・・（Expectation）そこで、まず k 回目の試行パラメータ θ(k)の元での Vij という拘束条件における Ψi の期待値 を求める。先ほどの空間（D）における Ψi の期待値である。Ψi が決まれば j における計算値が決まり、それは標準偏差 σ の正規分布の平均値であり、実測値 Vij がそれからどれ位隔たっているか（εij）が判るので、これで、分布確率の値が決まる。具体的には μ と Ω から Ψi での確率分布値が決まり、それに exp(-εij^2/2σ^2) を掛ければよい。これを Ψi を変えながら計算して Ψi を掛けて積分すれば、Ψi の条件付き期待値は計算可能である。実際には MCMC法で計算する。

・・・（Maximization）こうして Ψi の期待値が計算できると、それを Ψi として採用し、その拘束条件の元で、今度は θ を最適化し直す。今度は Ψ の分布を考える。そもそも Ψ は確率変数であり、パラメータ θ で固定効果と変量効果が判れば、Ψ の確率分布が決まるが、これは多次元の対数正規分布であるから、その中の確率変数として各個人の Ψi が与えられたという条件での θ についての尤度 L(Ψ|θ) を最大化することは容易である。つまり、Ψi の（実際は対数正規分布なので exp(Ψi）の）平均値（の対数）が固定効果で、その分散が変量効果である。こうして、新しい θ(k+1) が決まる。これが決まれば、最初のステップに戻って、以下繰り返して収束させる。

・・・・・・・・・・・・
●結合モデルへの拡張
・・・・・・・・・・・・
      実際に Marc et al. や Neant et al. の使っているモデルには、もう一つ上の階層があって、ウイルス量が更に、二次感染確率あるいは死亡率に関係づけられている。従って、分布パラメータ θ にはそのための固定効果が追加される。例えば、 Marc et al. であれば、二次感染確率を表現する為に導入された γ である。対応する観測データは感染したか、しなかったかという二値データとなる。感染したという観測データであれば、それはその時の Vij と試行解 γ(k) によって決まるロジットから感染確率が計算できるのだから、それがEstimation 計算時の確率分布値に掛かることになる。