R.M.May & A.L.Lloyd, "Infection dynamics on scale-free networks", Phys. Rev. E, 64(6), 066112(2001)
・・・スケールフリーネットワークというのは、それぞれの node(節)が k 個の他のノードと結合していて、そのような node の比率 P(k) が k^-ν となるようなネットワークである。ここでは k の下限を m としている。ここでは、その node を人間とみなし、結合(edge)を感染可能な接触とみなすことで、感染症の拡がり方を議論する。従来このモデルは SIS モデル、つまり感染が治癒しても免疫を持たないモデル、で議論されてきたが、ここでは SIR モデル、治癒すると再感染しない、というモデルで議論する。
・・・治癒率 γ を想定する。D=1/γ は平均感染力保持時間となる。
・・・それぞれの node は感受性(未感染)者、感染者、治癒者 に分類される。結合数 i を持つ未感染者の全数に対する比率を xi、同感染者の同比率を yi とする。残りが治癒者である。
・・・大きな仮定として、平均場近似を採る。つまり、未感染者 xi の結合先の node はいつも全体の比率に従った分布をしているという仮定である。(これを外すと確率的な計算機シミュレーションをするしかなくなる。)その平均場近似を使えば、Σ を j での和として、
dxi/dt = -xiΣβij・yj
dyi/dt = xiΣβij・yj - γyi
と書ける。これは通常の SIRモデルを結合数で分別したモデルである。そこで使われる感染係数 β が感染・被感染の対(ij)に依存している。しかし、個々の(1:1の)感染確率は変わらずに β であるとすれば、
βij = ijβ/<k>
となる。つまり、結合数 i を持つから i 倍されるのであるが、相手が、j である確率は jP(j)/ΣkP(k) となるから、もしも yj = P(j) (j グループでは全員感染)であれば、これに個々の感染率 β をかけた速度で感染が起きるが、実際は yj であるから、ijβyj/<k> の速度で感染が起きる。(< > は期待値を意味する。)しかし、感染を受ける方は xi の比率でしか存在しないので、結局 xi・ijβyj/<k> の速度で xi が減少する。
・・・ρ0 を βD<k> と定義しておく。これは、感染係数×平均感染力保持時間×平均結合数であるから、均一な接触を想定した通常の感染モデル(SIRモデル)においては、基本再生産数を意味する。しかし、接触数(結合数)に統計的分布を想定したネットワークモデルにおいては、平均接触数よりも大きい接触数を持つ場合の感染がより多く起きるので、接触数の分散にも依存して、
R0 = ρ0(1+Cv^2) = ρ0<k^2>/<k>^2
となることが判っている。ここで、Cv は結合数の分散係数で、
Cv^2 = <k^2>/<k>^2 - 1
である。つまり、初期の感染力は接触数分散が有る場合には SIR モデルよりも高いように振る舞い、感染が接触数の大きい人達に拡がってくると、自然に感染力が下がっていくかのように振る舞う。しかし、ここではそのような時間経過については解析していない。
・・・この論文での解析の主目的は最終的な感染者数比率である。勿論、それが少なければ標準的な SIR モデルによる自然感染の成り行きよりは早い感染終息であることが言える。上記の方程式から、最終的な感染者数比率 I は
I = < I - exp(-kα) >
α = ρ0 < k(I - exp(-kα)) >/<k^2>
・・・ここで、 < > 期待値の計算の為に k を連続変数とみなす。また ν= 3 の場合を計算する。
そうすると和は積分で近似できて、
<k> = 2m ; <k^2> = 2m^2・ln(kmax/m)
となり、もしも感染集団が無限大のサイズだと、kmax→∞ が可能となり、分散がログ発散するので、感染の侵入を防ぐ閾値が無い。
φ=mα と定義して、
2/ρ0 = {1-exp(-φ)}/φ + E1(φ)
これを数値的に解いて φ を求めれば、
I = 1 - 2E3(φ)
として、最終感染者比率が得られる。
ここで、En(φ) は φのn次の指数積分というものだそうで、数学公式集にある。
En(x) = ∫ (1/x^n)exp(-φx)dx : 積分は 1 から∞。
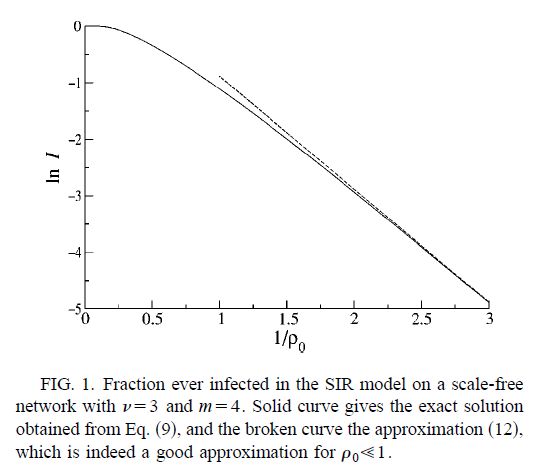
これが Fig.1 に描いてある。縦軸は ln(I) であるから、ρ0→∞ で I = 1、つまり全員感染である。
ρ0 が小さくなると、最終感染者比率 I は指数関数的に 0 に近づく(I ~ exp(-2/ρ0))が、明瞭な閾値は無い。
(注)
・・・比較の為に普通の SIR モデルの場合、I は、
1 - I = exp(-R0・I)
の解である。R0<1 では I=0 となる。
(注おわり)
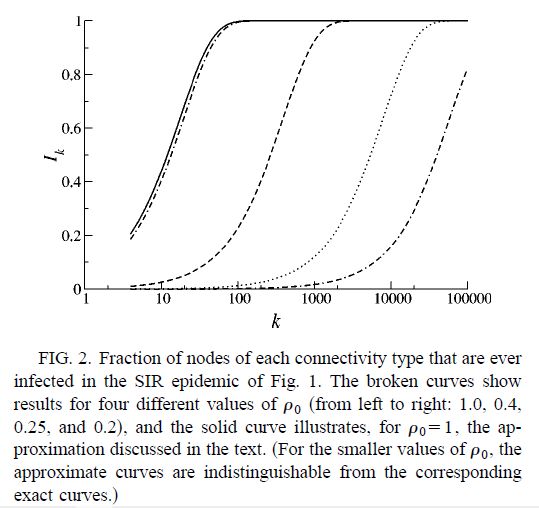
・・・個々のグループ k(k個の結合を持つ node )毎の最終感染者比率も計算できる。Fig.2 に図示してある。当然ながら結合個数の多い node、つまり、人との接触が多いグループ程最終感染者比率が大きい。グラフは横軸 k が対数目盛となり、左から、ρ0 = 1,0, 0.4, 0.25, 0.2 である。これらはいずれも 均一接触確率を仮定する SIR モデルでは現れない。
・・・νが2と3の間の時にも同様であるが、ρ0 が小さくなるときに、最終感染者比率 I は指数関数的ではなく、べき乗的に小さくなる。I ~ ρ0^(1/(3-ν))。
・・・人口サイズが有限であれば、k は有限である。この時、ν= 3 であれば、
R0 ≒ (1/2)ρ0・ln(kmax/m)
となる。kmax/m ≒ N^(1/3) と推定され、
R0 ≒ (1/6)ρ0・ln(N)
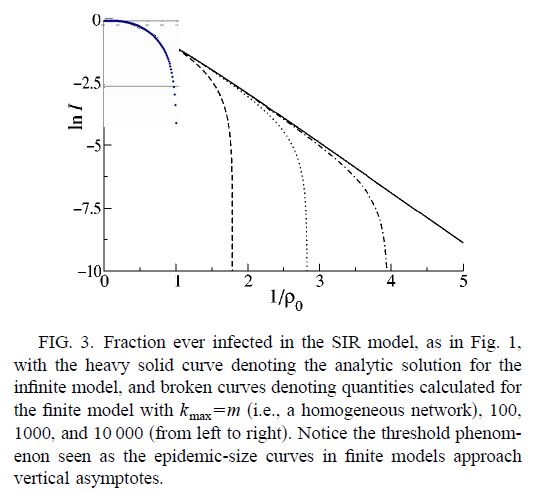
Fig.1 に対応する図が Fig.3 である。一番上の実線は Fig.1 の場合で、kmax=∞。
この図の説明では、kmax=m(均一結合数分布)、kmax=100、1000、10000 という4つがあることになっているが、kmax=4 の曲線は描かれていないようである。それは従来の SIR モデルであるから、1/ρ0 < 1 でしか値を持たない。計算して追加しておいた。
・・・この論文では、結合数(接触頻度)に分布があって、それがべき乗分布である場合について、それでも接触状況は結合数毎に平均化されている、という平均場モデルとなっているのだが、実際の社会状況を考えると局所的なネットワーク構造がある。つまり人はある程度の範囲での接触をしているから、完全には平均場近似が成り立たない。そういう場合の計算も行われていて[17,18]、ここでの解析と比較して、感染当初では感染が広がりやすいが、最終感染者比率は小さくなる、という結果が得られている。いずれにしても、接触頻度の高いグループの果たす役割が非常に大きいので、それを早く見つけ出して対策を講じるべきである。