マルカート方式だと、βを大きくすれば細かい波が平均化されて消えていくから、選択が容易である。ただ、自乗偏差は大きくなる。なお、全人数は保存するので、使われなかった固有ベクトル分の人数は全体を何倍かにして補正する。
2021.02.18
発症日ベースの新規感染者数推移から感染日ベースの推移へと変換するのは、簡単かと思ったら、厳密にやろうとすると、なかなか難しいことが判った。(まあ、実用上はそれほど厳密性に拘らなくても良いと思うけれども。。。)潜伏期間分布 c(t) の拡がりが 1 ~ L日 まであるとすると、観測された発症日ベースの人数 y(t) と未知数の感染日ベースの人数 x(t) の間には、
y(t)=∑s c(t-s)x(s)
の関係がある。ここで、t-s が 1~L だから、観測日数を M とすると、y(t) は t が M 個あり、x(t) としては、t が N= M+L-1 個必要となる。つまり、方程式が M個で、未知数が N+L-1 個である。これでは解が未定となる。(こういうのは 「逆問題」 と呼ばれている。)
なお、以下の計算には、潜伏期間分布として、1日後から20日後まで、順に、0.01 0.04 0.05 0.07 0.08 0.09 0.09 0.09 0.08 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.02 0.01 0.01 0.01 とした。これは下記の新しい文献からスプライン補間して求めた。https://advances.sciencemag.org/content/6/33/eabc1202.full である。全体に従来の潜伏期間よりも1~2日長い。発症者数データは、神奈川県・埼玉県・千葉県の2月24日~5月13日(80日間)を使った。
●特異値分解法
こういう時には特異値分解を使えば良いのではないか、と思って、試みている。Aij を c(i-j) とする。インピーダンスCT(解析プログラムは2001年に開発 )で使ったときは行数の方が多かったが、 ここでは列数の方が多い。いずれにしても、解の側に何らかの不定性があるために、解が安定的に求められなくなるという意味で共通性がある。一応、特異値分解の説明をしておく。
Aij = Σk Uki Dk Wkj
これが一般実行列(M行N列とする)の特異値分解であり、必ずできる。Dk が固有値、Uki が k 番目の左固有ベクトル Uk の成分 i、Wkj が k 番目の右固有ベクトル Wk の成分 j である。それぞれ正規直交条件を満たしている。k の数は i と j の少ない方だけある。今は、M個である。上の式の両辺に Wk'j を掛けて j で和を採ると、Wk の直交性から、
Σj Aij Wkj = Dk Uki
となることから判るように、未知数 xj の作る N次元空間内のベクトル Wk と 既知数 yi の作る M次元空間内のベクトル Uk とは1:1の関係で結びついていて、その長さの比例係数が Dk である。xj はベクトル Wk によってその全空間の内一部 M次元が展開され、一方 yi の方は完全にベクトル Uk の一次結合によって表現される。yi の Uki 成分を求めて、それを Dk で割れば、対応する xj の k 成分が得られるから、
ak = ∑i Uki yi
xj = ∑k ak Wkj/Dk
とすれば、xj が得られる。ただし、Wk で表現できない空間次元(余剰の N-M次元)の x 成分を加えても、y には影響しないから、その分だけ解が不定となる。
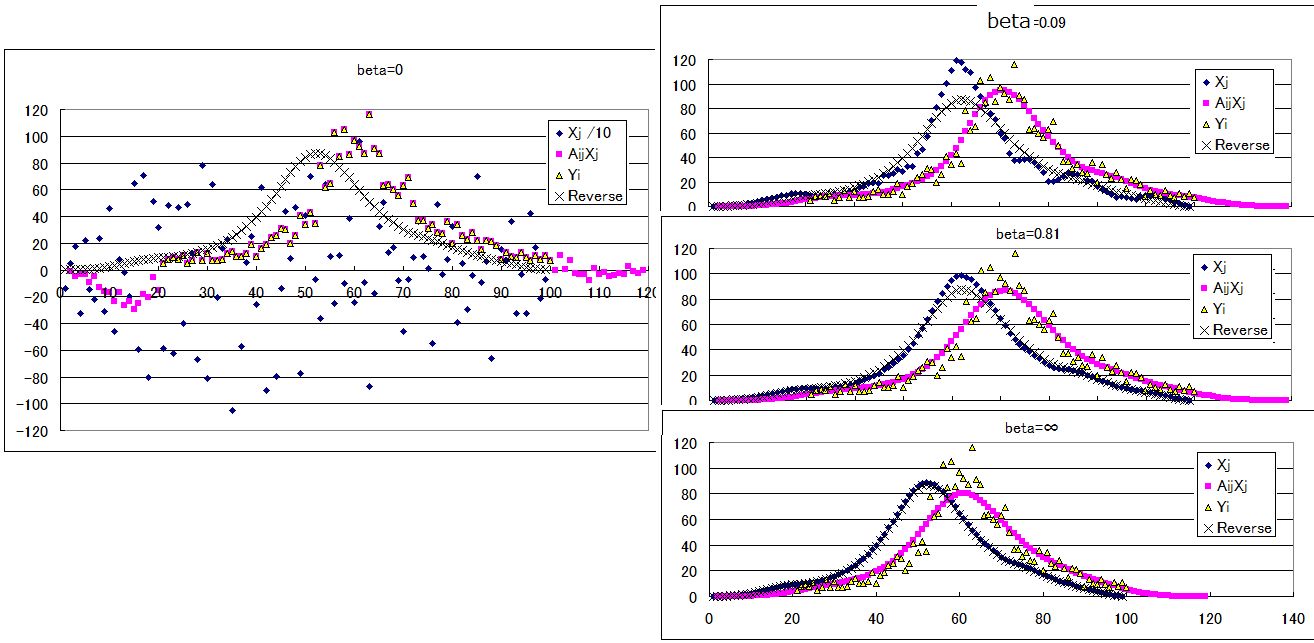
実際に解いてみたら、確かに yi を再現する xi が得られるが、相当にばらけていて、符号もいろいろである(次の次の図でβ= 0)。 後で説明する マルカート法に対応した固有ベクトル選択方法は、重みとして、
Rk=Dk^2/(Dk^2 + βD1^2)
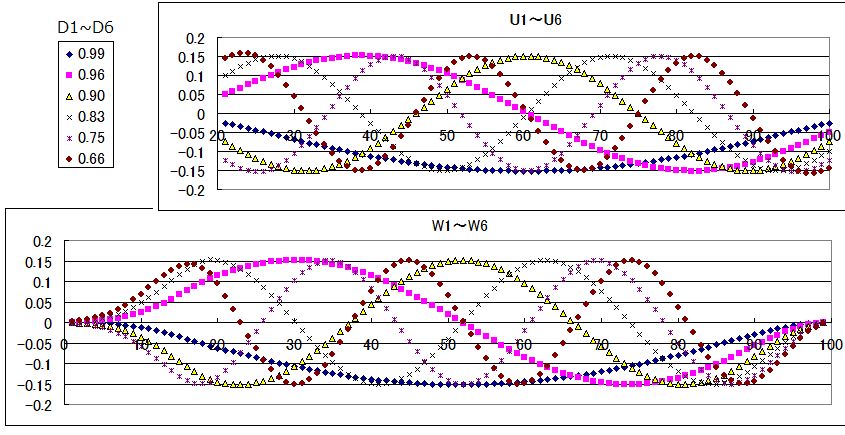
として、β をいろいろと選択する、というものである。 ここで D1 は最大固有値である。サンプル数を増やしながら、種々の固有ベクトル選択を試してみた。固有値の大きい方から一定数を取り出して使う方法と、マルカート法的に少しづつ寄与を変えていく方法(上記 β)を試してみる。前者の方法だと、癖のある振動が残ってしまう。固有ベクトルを見ると、これは一種のフーリエ成分のようなものであることが判る。つまり、固有値の大きさ順に並べると波長が短くなっていく。途中で切り取るとその辺りの波が強調されてしまう。下図は潜伏期間に 1日~20日までの分布を与え、観測発症日として21~100日のデータを与えた場合である。固有値の大きい方から6個示した。

マルカート方式だと、βを大きくすれば細かい波が平均化されて消えていくから、選択が容易である。ただ、自乗偏差は大きくなる。なお、全人数は保存するので、使われなかった固有ベクトル分の人数は全体を何倍かにして補正する。
そもそも、潜伏期間分布関数というのは、感染日から発症日までの日数データを集めてその頻度分布を作ったものだから、感染日から発症日を推定するための分布とも言えるが、逆に発症日から感染日を推定するための分布とも言える。だから、何も難しく逆変換する必要はないとも考えられる。(ただし、こういう解釈は一般的ではないようである。。。)つまり、
xj=∑i Aij yi
としてもよい。こうして得られた解 xj(Rev) をReverse解と呼ぶことにして、βによって特異値分解の固有ベクトルを限定して求めた解 xj(β) と比較した。青い菱形が解、赤い四角がその解から得られる発症数、黄色い三角が実測の発症数、×印が Reverse解である。β を大きくしていくと、波長の短い振動が抑え込まれて、次第に xj(Rev) に近づき、β=∞ にすると、一致してしまった。つまり、xj(Rev)=xj(β= ∞)
これを解析的に確認してみよう。β=∞ ということは Rk=Dk^2/(βD1^2) ということであるが、解 Xj は最終的には感染者数と発症者数が同じになるように定数倍されるので、定数因子は考えなくても良い。つまり、Rk=Dk^2/D1^2 となり、これは Dk を 1/Dk に置き換えることに相当する。
Aij=∑k Uik Dk Wjk
が特異値分解であるから、
Bij=∑k Uik (1/Dk) Wjk
として Bji を定義すれば、
yi=∑j Bij xj(β=∞)
となり、
xj(Rev)=∑i Aij yi
である。xj(β=∞)=xj(Rev) ということは、t(A)=(B)^-1 を意味する。t()は転置行列を意味する。
∑l AilBjl=∑l{∑k UikDkWlk}{∑k' Ujk'(1/Dk')Wlk'}
=∑kk' UikDkUjk'(1/Dk)Σl WlkWlk'
=∑k UikUjk=δij
となるから、予想通り、A と t(B) とは互いに逆行列であることが判る。要するに、β=∞ という Reverse解を一番解像度の悪い推定として、βを小さくしていけば、解像度を上げることができる、という判りやすい解法になっている。問題は解像度をどこまで上げれば良いのか? である。これには答えが無い。
●特異値分解とマルカート法との関係
マルカート法は、おそらく最も効率的な非線形最小自乗法である。もともと、Yi と 関数 Fi (X)から、
∑i{Fi(X) - Yi}^2
を最大あるいは最小にするような (X) を求める。今の場合は、関数 Fi が線形関数:∑j Aij Xj になっていると考えれば良い。線形であれば、上記のように連立方程式を解くことになるが、非線形であれば、∂Fi/∂Xj = Aij として、自乗和の Xj 微分から得られる正規方程式
∑j(Σi Aim Aij)ΔXj=∑i Aim ΔYi
を解き、Y の誤差 ΔY から X の補正 ΔX を求める。A が特異値分解されているとすると、この方程式は、
∑k (Dk^2 Wmk)(∑j Wjk ΔXj)=∑k (Dk Wmk)(∑i Uik ΔYi)
と変形されて、( ) の k 成分同士が Dk 倍の関係になっていることから、原理上正確に、ΔX が得られる。ところが、Dk が小さいような k に対しては、ΔY のその成分から ΔX の成分を求めると非常に大きくなってしまい、ΔY に少しでも観測誤差があると、容易に線形範囲を逸脱するので、解が振動発散する。そこで、正規方程式の対角成分に βD1^2 を追加すると、左辺に ∑j βD1^2 δmj ΔXj が追加されることになるが、直交性から、δmj=∑k Wmk Wjk と表現できるから、正規方程式は、
∑k {(Dk^2 + βD1^2) Wmk}(∑j Wjk ΔXj)=∑k (Dk Wmk)(∑i Uik ΔYi)
となる。すなわち、
X の k 成分(∑j Wjk ΔXj)= Dk Wmk(∑i Uik ΔYi)・Dk/(Dk^2 + βD1^2)
となって、Dk の小さな場合の寄与が縮小されて、安定化する。Dk で割る代わりに (Dk^2 + βD1^2)/Dk で割ることになるので、結局 k 成分の寄与が
Rk= Dk^2/(Dk^2 + βD1^2)
倍されていることになる。答えが暴れない程度に β を大きく採るので、どうしても主観性を免れない。逆に β を無限大にすると、正規化方程式が対角行列となり、ΔX=∑i Aim ΔYi、つまり Reverse解となる。
今回の問題では、F が線形であるから、Aij はイテレーションによって変わらず、ΔX は方向か変わらない。従って、イテレーションをするまでもなく、比例計算だけで最適解に到達する。ただし、β を小さくして誤差を小さくすると、観測値の誤差のために答えが大きな振動を起こすということである。
●特異値分解の余剰次元を使って感染者数を平滑化する方法
特異値分解法でそのまま解くと、xj が大きく変動するが、当然ながら、観測値 yi が厳密に再現される。yi=∑j Aij xj(β=0) である。固有ベクトルを制限することで、変動が収まる。極限まで変動を抑えると、逆解 xj(β=∞)=∑i Aij yi が得られる。次節での議論のように、本来最大尤度条件であれば、厳密に 観測値 yi を再現しなくてはならないので、パラメータ β を使った変動抑制は、実用的ではあっても「論理的必然性」には乏しい。そこで、xj の空間の中で使っていない、N-M=L-1 次元を考える。これは固有値が 0 なので、yi に対しては寄与が無い。つまり、この自由度を使えば、観測値の再現に影響することなく、xi の変動を制御できるかもしれない。ただし、特異値分解ではその空間は無視されるので、別途その直交規定ベクトルを取り出す必要がある。特異値分解で取り出した k=1~M(M<N)の固有ベクトル Wik (i=1~N) の全てと直交するような N-M-1個のベクトル Wik (k=M+1~N)を求めるには、シュミット法を使う。初期ベクトルとして、aik を与える。これは独立となるように採れば良い。具体的には対角行列とした。
Wik= aik - ∑(l=1~k-1) {(∑i' ai'k Wi'l)/(∑i' Wi'l Wi'l)}Wil
である。実際にM=80、N=99 でやってみたら、k が N に近い部分で直交性がかなり甘くなってしまったので、そのベクトルを初期条件として再度行うとうまく行った。
xi の変動を抑える為には、最小化すべき関数が必要である。そこで、滑らかな変動を示す逆解を選んだ。すなわち、(xj(∞) - xj(0) - Δxj)^2 とし、Δxj が k=M+1~N からの寄与である。
Δxj=∑(k=M+1~N) ak Wjk
である。未知数は ak であるから、これは最小自乗法で解くことができる。正規化方程式は、
∑j Wjk Wjk' ak' = ∑j (xj(∞) - xj(0))Wjk
となるが、∑j Wjk Wjk' = δkk' となるから、
ak=∑j {xj(∞) - xj(0)}Wjk
となり、
Δxj=∑(k=M+1~N){∑j' {xj'(∞) - xj'(0)}Wj'k Wjk}
=∑j'{∑(k=M+1~N)(Wj'k Wjk)}{xj'(∞) - xj'(0)}
{∑k } 内は予め計算しておける。
実際にやってみたら、驚いた。Δxj=0 になった!
考えてみれば当然である。xj(0) も xj(∞) も、一般的に xj(β) も全て、k=1~M の空間内のベクトルである。それと k= M+1~N の空間のベクトルは直交しているから、何の寄与も出来ないのである。プログラムの確認が出来たという事になる。
滑らかさの尺度として、何か別な関数を考えねばならない。 隣接する xj 間の差異の自乗和を設定してみた。これは最小自乗法で解ける。しかし、殆ど効果が無かった。つまり、差異の自乗和を最小にしても xj 自身が殆ど変わらない。データ採取期間が長くなっても、余剰空間の次元は 潜伏期間の最大日数だから、その影響は小さくなるばかりである。つまり、これで明確になったのだが、感染者数の推移 xj の大きな変動の原因は観測値 yi のばらつきそのものにある。従って、先に観測値の平滑化をすべきだろうが、そうすると、そのやり方の根拠を問われる。そこで、観測値を確率現象として解釈する、という方法が必要になる。
● EMS法
ところで、現在標準的に使われている方法は Smoothed EM Algorithm と言われる方法らしい。西浦さんの解説の中で紹介されているが、どんな方法であるかについては触れていない。ネットで探したら、その 解説のブログ があった。下記の論文がオリジナルらしい。
N G Becker, L F Watson, J B Carlin, "A method of non-parametric back-projection and its application to AIDS data", Stat Med. 1991 Oct;10(10):1527-42. doi: 10.1002 sim.4780101005. PMID: 1947509 DOI: 10.1002/sim.4780101005
この論文は open access ではないので、どこか大学の図書館まで行かないと入手できない。ブログの解説によると、発症日での発症者数を Yt、感染日での感染者数の推定値(未知数)を λi として、潜伏期間分布 f(t-i) が所与とする。実測の Yt は パラメータ ∑i f(t-i)λi を持つ、つまり期待値が 時刻 t で予測される発症者数として与えられた、ポワッソン分布に従うと考えるのである。これは二次感染を解析した Cori et al. と同様の確率解釈である。
Yt ~ (∑i f(t-i)λi)^Yt exp(-∑i f(t-i)λi) /Yt!
である。Yt か継続的に観測されている日数を T とすると、この分布関数の t についての積が、(Y1,Y2,Y3,,,,YT) の実現する確率であり、逆に、その一連の Yt が観測された時には、これが パラメータ ∑i f(t-i)λi の尤度分布である。対数を取って尤度を最大にすることを考えると、
対数尤度(λi)=∑t Yt ln{∑i f(t-i)λi} - ∑i f(t-i)λi
である。(定数項は省略)
これを直接最大化するのは難しいので、Expectation-Maximization-Smoothing 法というので、イテレーションで λi を求めたということらしい。旧 λi から 新λi を求める式が書いてあるが、当然理解できないので、僕としては、まず直接最大化することを試みる。つまり、対数尤度を λi で微分して 0 とする。
t の和が 1 から T であり、i の和が 1 から t であることに注意すると、i<t<T。
∂(対数尤度(λ))/λi = ∑(t=i~T) f(t-i)[Yt/{∑j f(t-j)λj} - 1] = 0
となる。∑t の中身は同じ式で、t の和の始まりが i なので、順に引き算すれば、
∂(対数尤度(λ))/λi - ∂(対数尤度(λ))/λ(i-1) =f(i-1)[Yi/{∑j f(i-j)λj} - 1]=0
が得られ、{ } 内が 0 ということになり、
Yi=∑j f(i-j)λj
という連立方程式が得られる。まあ、当然とも言えるが、これは僕が特異値分解で解いたのと同じ方程式(f(i-j);λj → Aij;Xj)である。一般的に i の数が j の数より少ないので、解は不定となるから、特異値分解によって、感度の高い成分を取り出したのである。
このやり方だと、
∑i{Yi - ∑j f(i-j)λj}^2
を最小化していることになり、本当にゼロまで最小化していれば、対数尤度を最大化していることになるのだが 、不要な振動を除くためにそれが出来ないので、その場合に、 対数尤度の最大化とどういう関係にあるのか?
Vt=∑j f(t-j)λj
と書き直すと、対数尤度の最大値は、T次元空間 (V1,V2,,,VT) の中の Vt=Yt という点にある。その点の周りで、対数尤度を展開すると、
対数尤度≒∑t {Yt ln(Yt) - Yt - (1/2Yt)(Vt - Yt)^2 } + ・・・
となる。つまり、最小自乗法というのは、対数尤度を最大値からの2次形式で近似している、ということである。
ということで、EMS法について勉強してみることにした。とりあえず、別の同等な文献を探さねばならない。