K51.放射冷却量予測の簡便法(津山)
著者:近藤 純正
夕方から朝までの冷却量は、夕方の有効放射量と一般風の風速、及び地表層の熱的パラメータに
よって決まる。ここでは数100mスケールの狭い範囲の気温冷却量を「地表面の放射冷却の原理」
に基づいて、夕方の気温と相対湿度から予測する。実例として、岡山県内陸の代表地点・津山観
測所用の簡便図作成までの手順を示した。作成した簡便図は図51.7(晩秋用)と図51.8(初春用)
である。今後、津山の基本データに基づいて作成する津山周辺のアメダスについては次の章で説明
する。
(完成:2011年2月8日)
本ホームページに掲載の内容は著作物であるので、
引用・利用に際しては”近藤純正ホームページ”からの引用であることを
明記のこと
更新の記録
2011年2月2日:図の一部を掲載
2011年2月7日:ほぼ完成
2011年2月8日:完成
目次
51.1 はしがき
51.2 有効放射量と放射最大冷却量
51.3 風あり関数の決定
51.4 熱的パラメータの決定
51.5 冷却量予測の簡便図の作成(津山)
51.6 検証
まとめ
参考文献
51.1 はしがき
おもな記号:
a(m/s): 風あり関数の係数、風速依存性を表す。
b=DTUh=0/DTmax: 快晴微風夜の無次元冷却量。b から熱的パラメータが求められる。
Cgρgλg(J2s-1K-2m-4): 地表層
(植物など地物を含む)の熱的パラメータ。熱的パラメータは気温の冷却量の実測値から
得た b 値によって求められる。
DT(℃): 冷却時間 t の冷却量。
DTmax(℃): 放射最大冷却量、夕方の有効放射量の関数。
Ku: 風あり関数(Uh=0でKu=1)。風速依存度を表す係数が a.
Kc=DT(曇天)/DT(快晴):冷却量の快晴夜に対する比。
L0(W/m2): 夕方の下向き大気放射量、夕方の気温と湿度の関数として表す。
t(s): 冷却時間、日没30分前を基準にした日出までの時間(季節による)、ただし諸係数を
決める準備解析では t=12時間を用いる。「秒」のかわりに図では「時間」で表示する。
T0(℃):夕方の気温、10分ごとの気温から前後合わせた5データの平均値。
rh(%):夕方の相対湿度、気温と同様に5データの平均値。0<rh<1であるが、図では%で
表示する。
Uh(m/s): 一般風の風速、900hPa面(高度1km付近)の風速、松江(米子)の高層資料を利用する。
w*TOP(kg/m2=mm) : 地上から大気上端までに含まれる有効水蒸気量(可降水量より20%程度小さい)
「地表面に近い大気の科学」のp.6の式(1.8)を参照。
σ(=5.67×10-8Wm-2K-4):ステファン・ボルツマン
定数.
σT04-L0(W/m2):夕方の有効放射量、
夕方の気温と湿度の関数として表す。
夕方の有効放射量:
夕方の有効放射量は、気温と地表面温度がほぼ等しくなる夕方には、近似的に夕方の正味放射量
Rn0に等しい。夕方の有効放射量は、大気全層の気温・水蒸気量とそれらの鉛直分布
に依存するが、放射に対しては下層大気に重みのかかった気温・水蒸気量の影響が大きく、近似的に
は地上の気温と水蒸気圧の日平均値の関数として表される。実用上、日平均値の代わりに夕方の気温
と水蒸気量(湿度)を用いる。
夜間の冷却量は夕方の気温と相対湿度で表すことができる。有効放射量が代表できる水平の空間
スケールは、20~30km程度であるので、一つの県内(または県内の地区)の地点については、
代表的な気象観測所(気象台、旧測候所)で観測された夕方の気温と相対湿度から推定した
有効放射量で代表する。ここでは岡山県内陸の津山周辺を対象とし、まずその代表地点の津山
観測所について放射冷却量予測の簡便図を作成する。
一般風の風速:
一般風の風速とは、地表面の冷却・加熱の直接的な影響を受けない大気境界層上端の風速であり、
高度1kmあるいは900hPa面の風速 Uh とする。冷却量に及ぼす一般風の影響は、晴天夜の気温
下降量(冷却量)から、あらかじめ求めておく。諸パラメータを決める準備解析が終わり、冷却量
予測の簡便図が作成された後の実用では、近傍のウインドプロファイラ観測による風速 Uh を利用
する(津山およびその周辺では、高松と鳥取のウインドプラファイラ観測を利用する)。
熱的パラメータ:
強風夜でなければ、地表面付近の空気塊がひと晩に移動する距離は10km程度であるので、
ここで考える地表層の熱的パラメータとは、対象地点から1km程度以内に重みのかかった地域
の平均的な熱的パラメータであり、土壌のほか草木の葉・小枝などの地物を含んでいる。
この熱的パラメータは、晴天夜の冷却量から推定できる。対象地点ごと、また季節によって変わる。
熱的パラメータは降雨後や積雪時には変化するはずである。積雪50cm以上で大きく変化することは
1980年代の解析で分かっている。降雨後、雨量によって変りうるという心がけは持たねばならないが、
当面は無視して解析する。最初から放射冷却に影響すると考えられる数多くのパラメータを用いて解析する
と、解析が困難になる。解析結果から、外れたプロットがあれば、それは何によるかを検討して、
その理由が見つかれば、それ相応の対処をする。
有効放射量の推定誤差やその他による誤差は、簡便法として、すべて熱的パラメータに含める。
そのため、ここで得られる熱的パラメータは簡便法に適用する際の実効的な値である。
簡便図の作成順序:
夕方の気温と相対湿度を用いる冷却量予測の簡便図は、次の順序で作成する。
(1)有効放射量と放射最大冷却量:日本各地に共通して利用できる。津山観測所の観測値に基
づいて推定された日々の値は、岡山県内陸の他の地点にも日々の値として用いる。
(2)風あり関数:地点ごと、ここでは津山観測所について作図する。
(3)熱的パラメータ:地点ごと、ここでは津山観測所についての値を求める。
(4)放射冷却量予測の簡便図:津山について季節ごと(10~12月と2~4月)に作成する。
51.2 有効放射量と放射最大冷却量
有効放射量の図:
有効放射量は、夕方の気温(絶対温度)、夕方の下向きの大気放射量、有効水蒸気総量、
夕方の水蒸気圧(e0)、夕方の相対湿度(rh)によって、次のいずれかの関数として
表される。
σT04-L0=σT04
(1-L0/σT04)・・・・・(51.1)
=f1(T0, w*TOP)
≒f2(T0, e0)
=f3(T0, rh)
f は関数を意味し、有効放射量は夕方の気温と湿度で表すことができる。
注意:より正確には、夕方の有効放射量は日平均の気温と湿度で表されるが、実用目的から
夕方の気温と湿度で表す。このことで生じる誤差は、熱的パラメータに含まれることになる。
つまり、熱的パラメータには、ほかにも様々な誤差を含む実効的なパラメータとなる。
これが、簡便法の特徴である。
「地表面に近い大気の科学」のp.50の式(1.36)、p.75の式(2.33)、p.114の式(4.6)、p.299の
付録Bの式
(A2.1)~(A2.6)を参照すれば、快晴時の大気射出率(同書の図2.23と式2.33)は次式に
より表される。
L0/σT04=0.59+0.038y+0.011y2
・・・・・・・(51.2)
ただし、
y=ln(w*TOP)
水蒸気圧:e=rh×eSAT・・・・・・・・・・(51.3)
飽和水蒸気圧(ティーテンスの実験式):eSAT=6.1078×10cT/(d+T)・・・・(51.4)
水面上: c=7.5, d=237.3
氷面上: c=9.5, d=265.3
単位は、 eSAT:hPa, T: ℃
露点温度:TDEW=[237.3×ln(e/6.11)] / [17.27-ln(e/6.11)]・・・・(51.5)
TDEW<-5℃の範囲で:
y=0.0622TDEW+1.958-b0・・・・・・・・・(51.6a)
-5℃<TDEW<23℃の範囲で:
y=0.0714TDEW+2.003-b0・・・・・・・・・(51.6b)
23℃<TDEW<30℃の範囲で:
y=0.0345TDEW+2.851-b0・・・・・・・・・(51.6c)
b0=2.3026×[1-(p/1013)1/2] ・・・・・(51.7)
p(hPa):観測地点の大気圧(津山の年平均地上現地気圧p≒1000hPaを用いる)
図51.1は縦軸に有効放射量、横軸に夕方の気温、パラメータとして夕方の相対湿度で表した
関係である。この図51.1と次の図51.2は、津山以外の全国どこでも利用できる。この図は、
たとえば「きょうは同じ快晴微風だのに、なぜ冷却が大きいか?」など、現象の理解に役立つ
ものであり、簡便図ができ上がってからの予測作業そのもでは用いない。
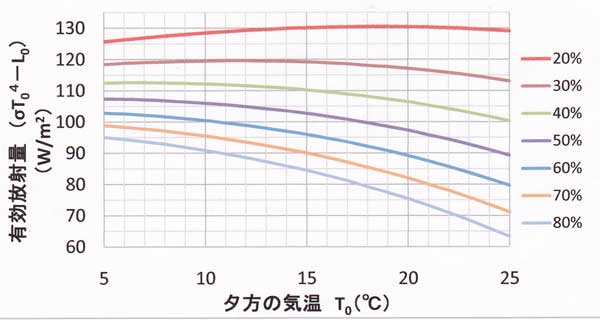
図51.1 夕方の気温と有効放射量の関係、パラメータは相対湿度(日本の各地で利用可能)。
(「研究の指針」の「K50.放射量予測の簡便法(概要)」
の図50.5に同じ。)
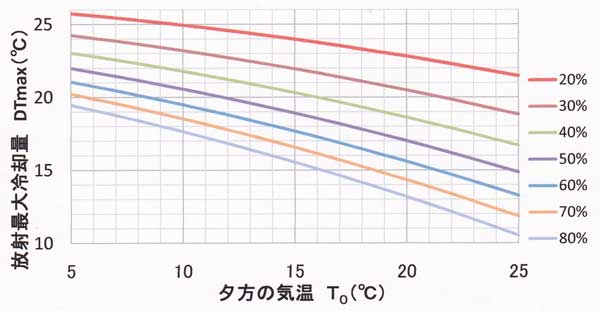
図51.2 放射最大冷却量と夕方の気温の関係、パラメータは相対湿度(日本の各地で利用可能)。
(「研究の指針」の「K50.放射量予測の簡便法(概要)」
の図50.6に同じ。)
放射最大冷却量の図:
放射最大冷却量は、冷却量の最大極限値を意味し、夕方の有効放射量を用いて次のように表される
(「地表面に近い大気の科学」のp.114の式4.6)。
DTmax=T0-TSC≒(T0/4)×
[1-(L0/σT04)]・・・・・・・(51.8)
TSCは、これ以下になることのない地表面温度の極限値である。
図51.2は放射最大冷却量を夕方の気温と相対湿度で表した関係である。
51.3 風あり関数の決定
風が吹く夜は、大気から地表面へ顕熱と潜熱(凝結・降霜)が供給されるために、風速の増加と
ともに冷却量は減少する。この減少率を表す関数が「風あり関数 Ku」である。
空気が非常に乾燥した夜は凝結・降霜ではなく蒸発となるので、簡便法ではこれがデータの
ばらつきの一因となる。
風あり関数は次の手順によって求める。
津山にもっとも近い高層気象観測所の松江(無人化前は米子測候所)で観測された900hPa面の
21時と翌朝9時の風速の平均値を Uh とする。
一方、快晴夜の夕方から12時間後までの気温低下量を冷却時間12時間の冷却量(DT12)とし、
放射最大冷却量DTmaxで割り算した無次元冷却量をDT12/DTmaxとする。12時間の冷却量は次式によって
求めた。
DT12=夕方の気温-12時間後の気温
夕方の気温は日没30分前の気温ただし10分ごとデータの前後合わせて5データの平均気温とし、
12時間後の気温も同様に10分ごとデータの前後合わせて5データの平均気温とした。
これは乱流的に変化する気温の瞬間値を用いると誤差となるので、ばらつきを小さくするためである。
風あり関数の決定に際して12時間の冷却量を求める理由は:
(1)冷却時間が季節(10~12月と2~4月)によって変わり、解析方法が複雑になるので、
冷却時間を短いほうに合わせて一定の12時間とした。
(2)津山では朝方霧が発生するなどにより、気温の下降傾向が途中で変化するデータを除外すると、
風あり関数(熱的パラメータでも同じ)を決める際のデータ数が少なくなる。
しかし、最後に作成する冷却量予測の簡便図は、季節に合わせて 14 時間用(10~12月)、
及び 12.5 時間用(2~4月)を作成する。その理由は、朝方に霧が発生するなど予測できない場合
でも利用するからである。
無次元冷却量と風速 Uh の関係を作図する際に、快晴夜のデータ数は20日以上を用いるべきだが、
今回は各シリーズ(10~12月、2~4月、弱凍結条件、凍結条件)について10日以下の少ないデータ数
で解析してみる(表51.2参照)。通常より少ないデータ数で解析する場合は、次の工夫が必要となる。
無次元冷却量DT12/DTmaxは熱的パラメータと関係する。そこで、縦軸(DT12/DTmax)を
対数目盛に選べば、熱的パラメータの異なるシリーズごとに関係グラフは縦方向に平行移動させても
関係グラフの形は変わらない。
図50.3のように、左に縦軸が対数目盛の図、右に縦軸が直線目盛の図を並べる。左の図で同シリーズ
(10~12月)のプロット群と異種シリーズ(2~4月、弱凍結条件、凍結条件)のプロット群を比較し
ながら4本の線の形(つまり風あり関数のUh 依存性)を試行錯誤で描いて決める。
関数形の形(曲線の形)が決まれば、右の図から Uh=0のときの縦軸の値 b=(DT12Uh=0/DTmax)
を読み取る(もちろん、対数目盛りの左図から b 値を読み取ってもよいが、感覚が異なるので
対数目盛りに慣れるまでは読み取りに注意が必要である)。この読み取った値 b から、次に説明する
熱的パラメータを決めることになる。
シリーズごとに読み取った b 値は後掲の表51.2に示した。
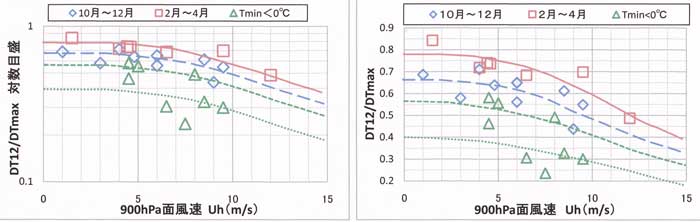
図51.3 冷却時間12時間の無次元冷却量と風速の関係、各シリーズごとに記号分けしてプロット。
左図は縦軸が対数目盛り、右図は縦軸が直線目盛り、両図に同じデータをプロットしてある。
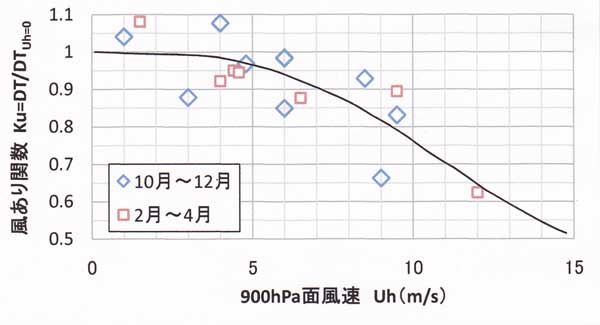
図51.4 風あり関数の風速依存性、秋シリーズと春シリーズのデータを記号わけしてプロット
してある。
データ数の多いほうの10~12月シリーズと2~4月シリーズについて、 Uh=0 のときの縦軸の
値 b=(DT12Uh=0/DTmax)が1になるように各データを規格化して図50.4にプロット
すれは「風あり関数 Ku」 が風速 Uhの関数として決まる。
Uh=0 でKu=1であり、Uh<3m/s の範囲で冷却量は微風夜とほぼ同じ(Ku≒1)としてよいことがわかる。
Uh=10m/sでは微風夜の0.76倍と読み取れる。
風あり関数(冷却量の風速依存性)は上空の風速が同じでも、その近傍100mスケールの地形
その他によって変わるので、地点ごとに求めなければならない。
「風あり関数 Ku」 が地点ごとに違うことは、次式のハイパボリックタンジェントの係数 a で
比較する。
縦軸の無次元冷却量:DT12/DTmax=b × tanh(a/Uh)・・・・・・・・・(51.9)
注: 式(51.9)は、風あり関数の実験式である。風あり関数を表すために、指数関数など
簡単な関数の中からもっとも適当な関数を探したところ、 tanh 関数による近似がよいことがわかった。
最近ではエクセルでも tanh 関数が作図できるようになった。
1980年代に、すでにアメダス68地点(山形県20地点、宮城県19地点、福島県の29地点)について
係数 b とa は求めてある(近藤・森、1982)。a はこれら68地点のうち不正確な11地点を除く
57地点でa=4~19m/sの範囲にある。a が大きいほど風速依存性が弱いことを意味する。
津山は内陸であるが、丘の上に位置するためなのか a=10m/sとなり、これら68地点の係数 a と
比較すれば、中間的な値として得られた。
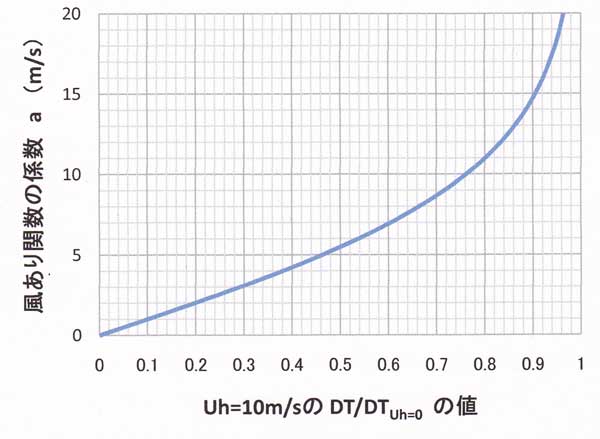
図51.5 風あり関数の風速依存性を表す係数 a を決める図。
図51.5は、「風あり関数 Ku」の図においてUh=10m/s のときの値(津山では0.76)から係数 a を決め
るための図である(全国で共通に利用できる)。図51.5の横軸=0.76から縦軸の値を読み取ると津山の値
として a=10m/s を得る。
注: もちろん、この図は使わずに各地点ごとに tanh の関数を作図すれば、その図から
係数 a、 同時に b も決まる。図51.5は tanh のグラフに慣れていない読者のために示したもので
ある。
係数 a は上空の一般風の影響を表す係数であるが、おおまかな地形だけからは判断し難い。
表51.1 風あり関数の数値表(津山)
上空の一般風速 微風夜に対する 上空の一般風速 微風夜に対する
Uh(m/s) 冷却の割合 Uh(m/s) 冷却の割合
0 1.00 8 0.86
1 1.00 9 0.81
2 1.00 10 0.76
3 0.99 11 0.70
4 0.98 12 0.65
5 0.96 13 0.59
6 0.94 14 0.54
7 0.90 15 0.50
51.4 熱的パラメータの決定
微風晴天夜の無次元冷却量は次式によって表される(「水環境の気象学」のp.147)。
b≡DT(t)Uh=0/DTmax = P(x) ・・・・・・・・・・・・・・・・・・(51.10)
P(x)≒[ 0.001+1.168x1/2+x ]/[ 1.062+1.725x1/2+x ]、 ただし0< x <64・・・・(51.11)
無次元時間:x =(4σT03)2 × (t/ Cgρgλg) ・・・・・・・
(51.12)
この P(x) の近似式は 0< x <64 の範囲で成り立ち、通常はこの近似式だけで十分である。
つまり、前節で求めた b 値から次の手順で熱的パラメータ Cgρgλg を知ることができる。
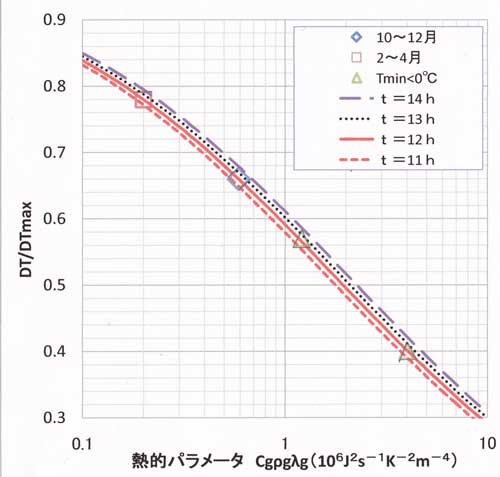
図51.6 無次元冷却量 DT(t)Uh=0/DTmax から熱的パラメータを決める図。パラメータ
として解析では様々な冷却時間(t=11時間、12時間、13時間、14時間)を用いることが
あるので、今回用いた12時間以外の線も描いてある。
図中の冷却時間=12時間の線の上にプロットした4点は、津山の各シリーズの値である。
図51.6は横軸に熱的パラメータ、縦軸にb=DT(t)Uh=0/DTmax、パラメータとして冷却
時間 t をとってある。津山の準備解析では t=12 時間の無次元冷却量 DT(t)Uh=0/DTmax
を用いたので、図51.6に示す4本の曲線のうち、t=12時間の曲線から津山の熱的パラメータ
Cgρgλgを読み取る。
表51.2は各シリーズについて得た熱的パラメータである。凍結時の熱的パラメータが大きく
評価されたのは、現実では凍結の潜熱が解放され冷却量が小さくなっているが、見掛け上では
熱的パラメータが大きく、熱慣性が大きいことになる。
表51.2 熱的パラメータ(Cgρgλg)と気温ほかの条件の表
シリーズ 夕方の 夕方の 翌朝の b= Cgρgλg
気温 相対湿度 最低気温 DT12Uh=0/DTmax
℃ % ℃ J2s-1K-2m-4
10~12月 15~24 44~65 2~14 0.66 0.6×106
2~ 4月 11~23 22~54 1~5 0.78 0.2×106
弱凍結 9~12 39~49 -0.2~-2 0.57 1.2×106
凍 結 0~5 54~63 -4 ~ -6 0.40 4×106
春(2~4月)の熱的パラメータが秋(10~12月)の値よりも小さいのは、植物など地物が乾燥し含有
水分の減少による可能性が考えられる。この可能性を確証するには、より詳細で精密な解析が
必要となる。
51.5 冷却量予測の簡便図の作成
以上の準備解析から熱的パラメータが分かったので、簡便図の作成に進む。
注:簡便図を描く手順
係数 a は風あり関数の形を表すもの、b は熱的パラメータを決めるために必要な係数であった。
熱的パラメータが決まったので、熱的パラメータと冷却時間 t を設定して簡便図の作成に取り
掛かる。
図51.7のように相対湿度をパラメータとした線を描くために、まず rh=0.3(=30%)として、
気温 T が5、6、・・・・25℃の時の有効放射量 →放射最大冷却量 →放射最大冷却量×P(x) →
放射冷却量が計算される →相対湿度30%のグラフを描く。今度はrh=0.4(=40%)として
同様に40%のグラフを描く。・・・・・・図が完成する。
簡便図は風速がゼロ(Uh=0)で冷却時間が t のときの放射冷却量DT(t)Uh=0を、夕方の
気温と相対湿度の関数として表すことである。前述の式を再び書けば次の通りである(「水環境の
気象学」の式6.64;「地表面に近い大気の科学」の式4.6)。
DT(t)Uh=0=DTmax ×P(x) ・・・・・・・・・・・・・(51.10)
無次元時間: x =(4σT03)2×t/ Cgρgλg ・・・・・(51.12)
DTmax=T0-TSC≒(T0/4)×
[1-(L0/σT04)] ・・・・(51.8)
放射最大冷却量 DTmax は前記の図51.2で示したように、夕方の気温と相対湿度で表される。
したがって、t 時間後の冷却量DT(t)Uh=0 は冷却時間 t と熱的パラメータCgρgλgを与
えれば計算できる(「身近な気象」の「M50.放射冷却の演習問題」
の演習2を参照)。
表51.3 放射冷却量予測の簡便図、または計算に用いる条件
シリーズ名 Cgρgλg 冷却時間
J2s-1K-2m-4 時間
10~12月 0.6×106 14
弱凍結 1.2×106 14
2~ 4月 0.2×106 12.5
弱凍結 1.2×106 12.5
凍結(12~1月) 4×106 14
注:冷却量予測の簡便図の作成では、表51.3に示す熱的パラメータと冷却時間を用いる。本章では、
おもに降霜が起こるか否かの秋と春についての簡便図を作成する。この方法で予測せずとも
最初から「弱凍結」ないし「凍結」がわかるような条件(夕方の気温が5℃以下)については
作図せずに、冷却量は上記の計算式から予測する。
表51.3に示す熱的パラメータと冷却時間を用いて前記の式(51.10)から、最終目標の放射冷却予測
の簡便図を作成した。
図51.7と図51.8はそれぞれ、津山の10~12月用と2~4月用である。
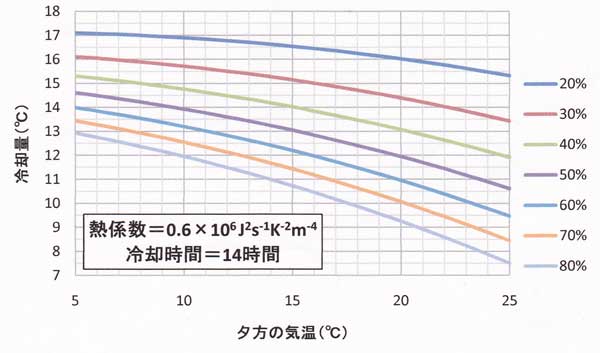
図51.7 放射冷却量予測の簡便図、津山の10~12月用。冷却時間=14時間、熱的パラメータ
=0.6×106J2s-1K-2m-4の場合。
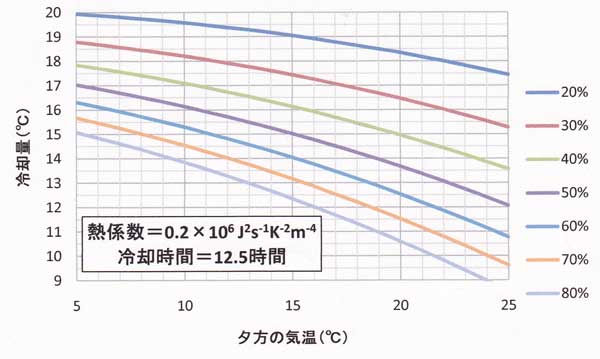
図51.8 図51.7に同じ、ただし津山の2~4月用。冷却時間=12.5時間、熱的パラメータ
=0.2×106J2s-1K-2m-4の場合。
参考:
ここでは凍結条件でも、熱的パラメータを見掛け上大きく用いて、冷却量を計算することとした。
これとは別に、凍結の影響を具体的に見るために、熱的パラメータを大きくせずに秋または春の
熱的パラメータを用いて計算冷却量と実際の冷却量の比較をしてみた。
図51.9は津山観測所の朝の最低気温が氷点下になった晴天夜間における冷却量の低下の割合である。
ただし、冷却量は風速 Uh によって変わるので、風あり関数によって補正し、風速ゼロのときの
冷却量に規格化した値で比較してある。
朝の最低気温が-4~-6℃の範囲の4点のプロットは、凍結の影響がないときの冷却量の約50%で
ある。これは別の章で見積もりしたように、10時間当たりに水の厚さ5mmの厚さが凍結し潜熱を解放
して夜間の冷却を抑制したことに相当している。水の厚さ5mmは凍結に寄与した土壌と植物など
地物に含まれる水を意味する(「放射冷却量予測の簡便図(概要)」の
50.4 補足的な事項-凍結の影響を参照)。
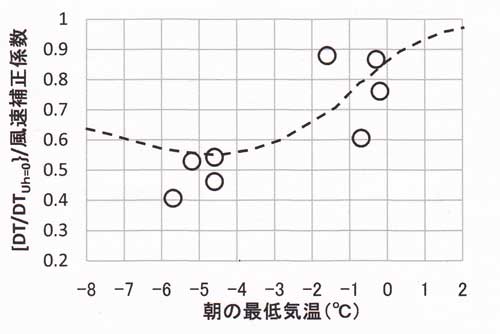
図51.9 朝の最低気温が氷点下の時の冷却量の低下の割合(最低気温が氷点下のときの冷却量/最低気温
が0℃以上のときの冷却量)。津山観測所の気温の冷却量から求めた関係、ただし上空の風速 Uh の
影響は補正してある。(「研究の指針」の
「K50.放射量予測の簡便法(概要)」の図50.13に同じ。)
51.6 検証
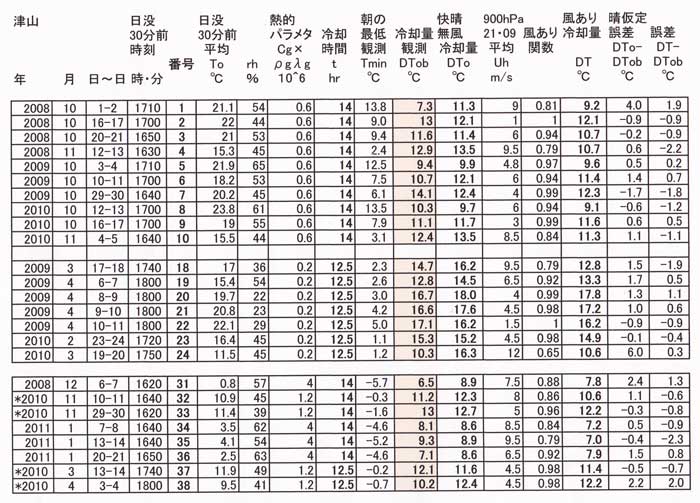
2008年10月~2011年1月の快晴25夜を選び、図51.7または図51.8から快晴微風夜の放射冷却量を読み取る。
次いで、一般風の影響を補正するために「風あり関数 Ku」の値を掛け算して風がある夜間の
冷却量 DT を求めた。今回は晴天夜のみの解析であるので、雲の影響は補正しない。
朝の最低気温が氷点下になる日は、上記の計算式から冷却量を求めた。
図51.10は横軸に資料番号を表し、縦軸は冷却量の予測値と観測値の差である。番号1~10は
10~12月、番号18~24は2~4月、番号31~38は朝の最低気温が氷点下、そのうちの弱凍結は番号
32~33と番号37~38である。
参考:
参考までに、弱凍結の条件については、図式と計算式による両方法で冷却量を求めた。ただし図式は、
秋または春の熱的パラメータを用い、計算式ではそれらより大きい熱的パラメータを用いた(表51.2
に掲げた熱的パラメータ)。
図51.10中の番号11~12と16~17の青色で塗りつぶした赤四角印は、凍結を考慮しない図51.7または
図51.8から求めたもので、予測冷却量が大きめに出ている。
赤色で塗りつぶした四角印または三角印(凍結条件の熱的パラメータを使用)は最終的な予測
誤差であり、±2℃の範囲内に分布している。誤差の標準偏差は10~12月で±1.2℃、2~4月で
±1.1℃、弱凍結と凍結条件で±1.4℃である。
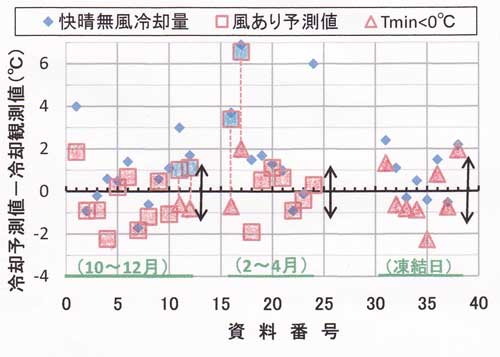
図51.10 冷却量予測値の誤差(=予測値ー観測値)。横軸は資料の番号(本文と表51.5を参照)、
赤で塗りつぶした赤四角印と赤三角印が最終的な誤差、小さい青印は快晴無風を仮定したときの
誤差、青で塗りつぶした赤枠四角印(全部で4プロット)は凍結条件の熱的パラメータを用いず
に秋または春の熱的パラメータを用いて予測した場合の誤差である。矢印は各シリーズの誤差の
幅を示す。
10~12月のデータにおいて、誤差の大きい番号1、4、7について夜間の10分ごとの気温を
みると、変動が激しいか、あるいは朝方の薄い霧(あるいは薄い上層雲)が晴れて急激に気温が
低下したと思われるデータである。こうした現象は予測できない、広い意味での不規則な変動であり、
誤差が大きくなるのはやむをえない。
一般に、乱流的不規則変動においては、統計的には標準偏差の3倍程度が最大誤差と想定しなければ
ならない。したがって、最大3~4℃の誤差が小さい確率で起こる可能性がある。
表51.4 気象条件と冷却量予測の誤差
シリーズ 誤差 データ数
℃
10~12月 ±1.3 10日
2~ 4月 ±1.1 7日
弱凍結・凍結 ±1.4 8日
表51.5 解析したデータ一覧
第一列の年に*印をつけたのは「弱凍結」の条件であり、冷却量予測は2つの方法で行った。
その1の方法は、秋または春の熱的パラメータを使用して図51.7または図51.8から求める方法、
その2の方法は、弱凍結の熱的パラメータを用いて計算式によって求める方法である。
この章では、快晴日のみを解析し、「微風晴天夜の冷却量」に風あり関数を掛け算して
「風あり冷却量」を求めた。
雲がある夜は、さらに図51.11の縦軸に示す係数を「風あり冷却量」に掛け算して
最終的な冷却量を予測することになる。
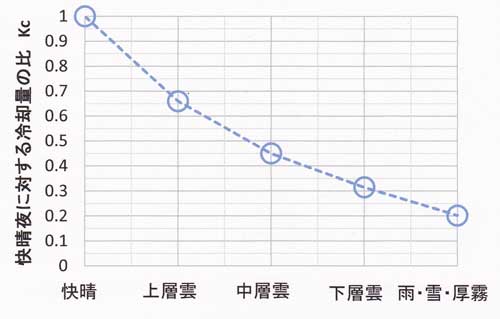
図51.11 快晴夜の冷却量に対する曇天夜の冷却量の比。上層雲で一面に覆われた夜の冷却量は
快晴夜の0.66倍、天空の半分が上層雲で覆われた夜は(1+0.66)/2=0.83倍の補正を行う。
(「研究の指針」の「K50.放射量予測の簡便法(概要)」
の図50.8に同じ。)
まとめ
(1)放射冷却量を夕方の気温と相対湿度から求める簡便な図(岡山県内陸の津山用の図51.7、
図51.8)を作成した。この作成の手続きの説明は、簡単ではなかったが、パソコンなどがなくても
冷却量の見積もりが簡単にできる。
図式によらずとも、冷却量は式(51.10)によって簡単に計算できるのに、なぜ簡便図を作成するか?
一般に、デジタル的な計算は能率的であるが、現象の理解の助けには図式のほうが優れている。
図式では、「今夜は冷却が大きそうだ!」と直感的に予測している現象の理解に役立つ。例えば、
「乾燥して低温ぎみだったので冷却が大きく何℃も下がったのだ」と図から理解できる。図式での
慣れは、直感力を強くするのにも役立つ。
(2)風あり関数を求めてみると、式(51.9)の係数として津山の値 a=10m/s を得た。この係数は
冷却量の風速 Uh に対する依存性を表すもので、1980年代に東北地方のアメダス68地点について得た
係数と比較すれば、中間的な値に相当する。
係数がa=10m/sという意味は、一般風の影響によって冷却量が76%以下に低下するのは一般風の
風速 Uh が10m/s 以上であるということである。仮にa=5m/s の場合は、Uh が5m/s 以上で冷却量
が76%以下に低下し、風速依存性が大きい地点である。
(3)快晴で夕方の気温が5℃以下のときは(表51.2)、土壌中や地物に含まれる水分が夜間に凍結し
潜熱の解放によって冷却量がおおよそ半分に抑制される。
このことから、凍結に寄与した水分は土壌内含水量に換算すると、水の厚さで5mmに相当する。
土壌の体積含水率=0.2 m3/ m3の場合には、土壌の厚さ25mm が
凍結したことに相当する。
(4)地表層(草木など地物も含む)の実効的な熱的パラメータを評価してみると、
秋と春はそれぞれ、0.6×106と0.2×106
J2s-1K-2m-4
と推定された。春の値が小さいのは、地表層が秋よりも乾燥していることによると考えられるが、
確証には詳細で精密な解析が必要となる。
(5)放射冷却予測の簡便図(凍結条件では作図していないので計算式)によって冷却量を読み
取り、それに図51.4の風あり関数を掛け算して得た夜間の風あり冷却量と、実測の冷却量
(=夕方の気温―朝の最低気温の観測値)を比較すると、誤差は±1.1~1.3℃(凍結条件の氷点下
では±1.4℃)となった。
(6)この章では快晴夜と判断された25日分を解析した(秋10日、春7日、凍結条件8日)。
(7)雲があるときには、快晴夜の冷却量に対する曇天夜の冷却量の比 Kc を表す図51.11を用いて
補正することになる。例えば、上層雲による薄雲がでている夜、あるいは夕方は晴れているが、
西のほうから上層雲が広がってきて数時間後から全天薄曇りとなりそうな夜は、快晴夜として求めた
冷却量に0.66倍を掛け算した値が冷却量になる。
(8)注意1: 今回の津山の解析では、秋と春の熱的パラメータを決
めるために用いたデータ数は、
それぞれ10日と7日で、いずれも少数日であり、簡便図作成に用いた熱的パラメータに誤差を含む
可能性がある。今後、実際に延べ日数10~20日以上について応用してみて、冷却量の誤差がプラス
またはマイナスに偏る傾向がでてくれば、パラメータの値がずれていたことになる。
その場合は、それらのデータも今回の準備解析に用いたデータに加えて、再度、熱的パラメータと
風あり関数を決め直すがよい。
(9)注意2: 今回は夕方から朝の最低気温(瞬間値)までの気温
下降量を観測値として、予測値との誤差を評価した。この誤差は、どこまで小さくすることが可能か?
近藤・森(1982)の研究によれば、朝の最低気温(瞬間値)の代わりに、乱流的変動を平滑する
目的で、最低気温が起こる時間帯の1時間平均気温を知る目的で予測したとしても、予測精度には
限界があり、誤差の標準偏差は±0.8℃程度であることを示した。
このことから、乱流的な変化で生じる最低気温の予測誤差の限界は、±1.0℃程度とみなさ
なければならない。
参考文献
近藤純正、2000:地表面に近い大気の科学.東京大学出版会、pp.324.
近藤純正(編著)、1994:水環境の気象学ー地表面の水収支・熱収支ー.朝倉書店,pp.350.
近藤純正・森 洋介、1982:アメダス(地域気象観測所)データを用いた夜間冷却量の解析と
最低気温予測式(1).天気、29、1221-1233.











