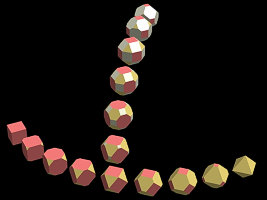
The 5 polyhedra on the uppest line are Platonic. Scene file : lpplhfrm.txt |
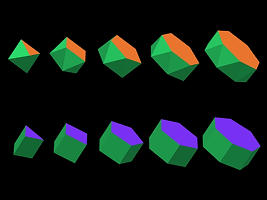
I got a family from hexahedron to octahedron which can be expressed by one function. Scene file : lpplhmd4.txt |
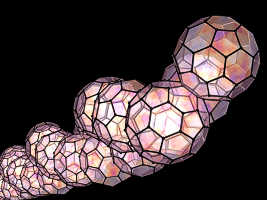
Scene file : lpplhmd5.txt |
Scene file : lpplhmdn.txt |
Scene file : lpplhchn.txt |
Scene file : lpplhrad.txt |