問題4-4-1 解説
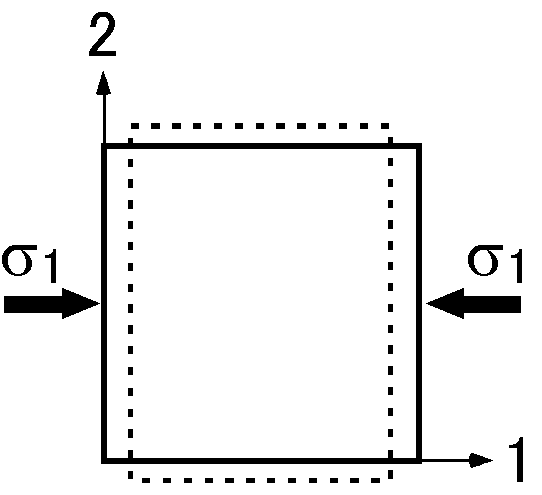
本文の式 (6) で \(\sigma_2\) = \(\sigma_3\) = 0 とおくと次のようになります. \begin{eqnarray} \sigma_1 & = & (\lambda+2\mu)\epsilon_1 + \lambda\epsilon_2 + \lambda\epsilon_3, \label{eq01} \\ 0 & = & \lambda\epsilon_1 + (\lambda+2\mu)\epsilon_2 + \lambda\epsilon_3, \label{eq02} \\ 0 & = & \lambda\epsilon_1 + \lambda\epsilon_2 + (\lambda+2\mu)\epsilon_3. \label{eq03} \end{eqnarray} 式 (2) から式 (3) を引くと, \[ 2\mu\epsilon_2 - 2\mu\epsilon_3 = 0, \] より, \[ \epsilon_2 = \epsilon_3. \] これを式 (2) または (3) に代入して, \begin{equation} \epsilon_2 = \epsilon_3 = -\frac{\lambda}{2(\lambda + \mu)}\epsilon_1. \label{eq04} \end{equation} この結果を式 (1) に代入すると, \begin{eqnarray} \sigma_1 & = & (\lambda + 2\mu)\epsilon_1 - \frac{\lambda^2}{\lambda + \mu}\epsilon_1, \nonumber \\ & = & \frac{\mu(3\lambda + 2\mu)}{\lambda + \mu}\epsilon_1. \label{eq05} \end{eqnarray} \(\epsilon_1\) で表わして, \begin{equation} \epsilon_1 = \frac{\lambda + \mu}{\mu(3\lambda + 2\mu)}\sigma_1. \label{eq06} \end{equation}
補足:ヤング率 \(E\),ポアソン比 \(\nu\),体積弾性率 \(K\) について
式 (5) と本文の式 (2), \(\sigma_{xx} = E \epsilon_{xx}\),を比較することでヤング率 \(E\) は, \begin{equation} E = \frac{\mu(3\lambda + 2\mu)}{\lambda + \mu}. \label{eq07} \end{equation} と表せます.また,式 (4) に含まれる次の式をポアソン比 \(\nu\) といいます. \begin{equation} \nu = \frac{\lambda}{2(\lambda + \mu)}. \label{eq08} \end{equation} ポアソン比は弾性体に法線応力を加えた場合の法線方向の歪みに対する横方向の歪みの比で,式 (8) から最大値は 1/2 です.式 (7) と (8) を用いると,式 (6) と (4) は次のように表せます. \begin{eqnarray} \epsilon_1 & = & \frac{1}{E}\sigma_1, \label{eq09} \\ \epsilon_2 & = & \epsilon_3 = -\frac{\nu}{E}\sigma_1. \label{eq10} \end{eqnarray} 式 (9) と (10) を合わせてフックの法則と呼ぶことが多いようです.また,体積変化 \(\Delta\) は, \begin{equation} \Delta = \epsilon_1 + \epsilon_2 + \epsilon_3 = \frac{1 - 2\nu}{E}\sigma_1, \label{eq11} \end{equation} となります.式 (11) からは, \(\nu\) = 0.5 の物体は体積変化がゼロとなり,そのような特性を非圧縮性といいます.また,流体では剛性率 \(\mu\) がゼロですので, \(\nu\) = 0.5 となります.地震学の観測から外核のポアソン比は 0.5 ですので,外核が流体であることが分かります.
体積弾性率 (非圧縮率) \(K\) については,本問題からは離れますが,3つの主応力がゼロでないとして,本文の式 (6) を3辺加えることで次式となります(本文で導きました). \[ K = \frac{3\lambda + 2\mu}{3}. \] この式を変形すると, \begin{eqnarray*} K & = & \frac{1}{3}\times\frac{\mu(3\lambda + 2\mu)}{\lambda + \mu}\times\frac{\lambda + \mu}{\mu}, \\ & = & \frac{E}{3}\times\frac{\lambda + \mu}{\mu}. \end{eqnarray*} ここで, \[ \frac{\mu}{\lambda + \mu} = 1 - \frac{\lambda}{\lambda + \mu} = 1 - 2\nu, \] の式を利用すると,体積弾性率 \(K\) は次式で表わされることになります. \begin{equation} K = \frac{E}{3(1 - 2\nu)}. \label{eq12} \end{equation} この式からは,ポアソン比が 0.5 の物体では体積弾性率は無限大となることが分かります.
以上の,ヤング率 \(E\),ポアソン比 \(\nu\),体積弾性率 \(K\),剛性率 \(\mu\),ラメの第1定数 \(\lambda\) は等方性弾性体の5つの弾性定数です.これらの中で独立な定数は2つだけで,任意に選んだ2つの定数で他の定数を表わすことができます.なお,ラメの第1定数 \(\lambda\) は理論上の定数で,測定は不可能で物理的意味もないそうです.