問題4−3−1 解答
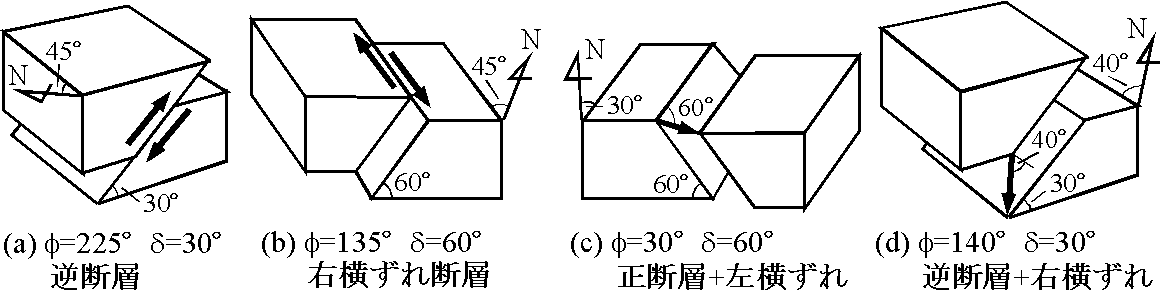
断層運動による発震機構は (1) から (4) については次の通りです.水平および下向きのスリップベクトルについては,その投影を記号 ♦ でプロットしました.スリップベクトルは,2つの節面のうち断層でない節面に垂直となることに注意する必要があります.即ち,スリップベクトルは断層でない節面の投影である大円の「極」を表わします.
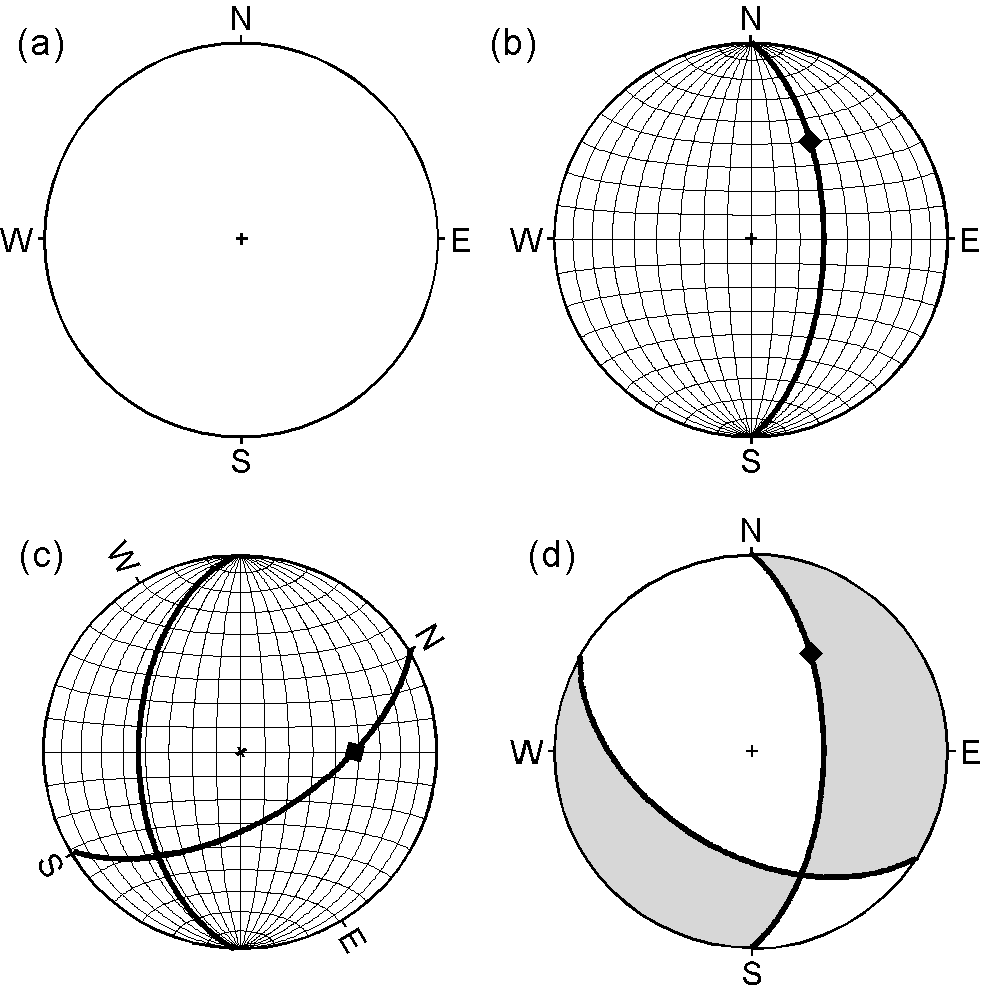
断層運動 (5) については,作図の様子を4段階に分けて説明しました.
- トレーシングペーパーにシュミットネットの外周(水平線)と中心(鉛直下方向)を写し取ります.
- トレーシングペーパーの NS を中心の経度線に合わせ,東に 60° 傾いた経度線を写し取ります.スリップベクトルの向きは,走行の方向から断層面内で 50° 時計回りの方向ですので,写し取った経度線上で極から 50° の点(極から5本目の緯度線との交点)に ♦ をプロットします.
- スリップベクトル ♦ がシュミットネットの赤道上に来るようトレーシングペーパーを回転し, ♦ から 90° 離れた経度線を描きます.この例では,スリップベクトルの水平面からの傾きは約 42° となるので, 10° 毎のシュミットネットでは該当する経度線はなく,比例配分を考えて手書きします.
- トレーシングペーパーの回転を元に戻し,押しの領域を着色します.
問題4−3−2 解答
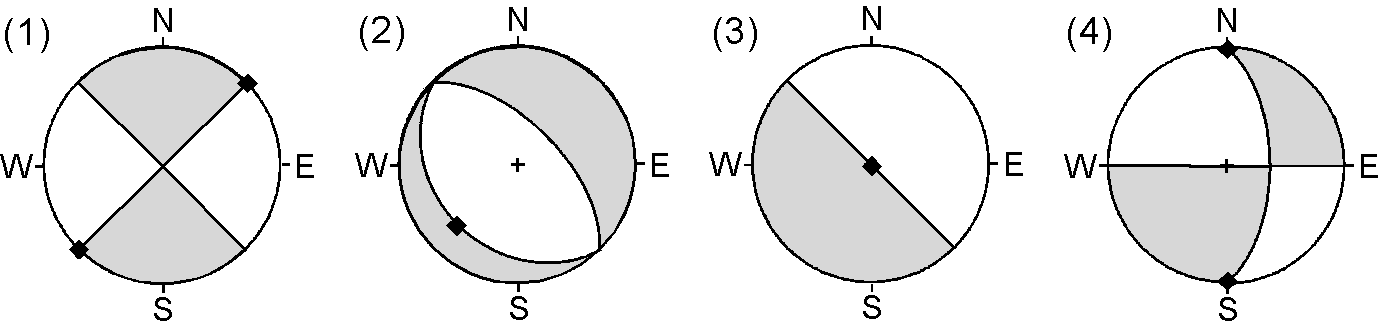
スリップベクトルを伴う節面が断層面ですので,どちらの節面かの判断は容易です.(a) では \([\phi=225°,\delta=30°]\) (N45°E30°NW) の面が断層で典型的な逆断層のパターンですが,傾斜が浅いので押しの領域が変形しています.(b) では \([\phi=135°,\delta=60°]\) (N45°W60°SW) の面が断層です.典型的な右横ずれ断層ですが,断層面が垂直でないので十字のパターンからずれています.(c) と (d) はそれぞれ \([\phi=30°,\delta=60°]\) (N30°E60°SE) と \([\phi=140°,\delta=30°]\) (N40°W30°SW) が断層です.これらは縦ずれと横ずれの両方を含み発震機構は複雑ですが,(c) と (d) はそれぞれ正断層と逆断層のパターンの変形と考えることもできます.
断層の見取り図の描き方は任意ですが,一例を下図に示します.なお,(c) と (d) では2つのスリップベクトルのうち発震機構にプロットされた下向きのベクトルだけを描きました.