問題４−２−１ 解答

（１） 正弦関数は周期が 2\(\pi\) の関数ですので，波長 \(\lambda\) は次のように求まります． \[ k(x + \lambda) = kx + 2\pi, \quad \Rightarrow \quad \lambda = \frac{2\pi}{k}. \] 同様にして， \[ \omega(t + T) = \omega t + 2\pi, \quad \Rightarrow \quad T = \frac{2\pi}{\omega}. \] なお， \(1/\lambda\) は単位長さあたりの波の数（山または谷の数）で，その 2\(\pi\) 倍の \(k=2\pi/\lambda\) は波数とよばれます．また， \(f=1/T\) は単位時間あたりの振動の数で振動数（周波数）とよばれます．振動数の 2\(\pi\) 倍の \(\omega=2\pi f\) は角振動数（角周波数）とよばれ，角速度と同じです．

（２） 正弦関数 \(\sin\theta\) の \(\theta\) は位相とよばれ，波の特定の位置を表わします．いま，時間の \(t_0\) から \(t_1\) への経過につれて (\(t_1\) > \(t_0\))，位置が \(x_0\) から \(x_1\) へ変化したとします．そこで，それらの位相を等置すれば，波の特定の位置の移動速度 \(v\) が分かります． \(\sin(kx - \omega t)\) については， \[ kx_1 - \omega t_1 = kx_0 - \omega t_0, \quad \Rightarrow \quad x_1 - x_0 = \frac{\omega}{k}(t_1 - t_0). \] \(t_1 - t_0\) は正ですので，波は \(x\) の正の方向へ伝わることが分かります．伝播速度は， \[ v = \frac{x_1 - x_0}{t_1 - t_0} = \frac{\omega}{k}. \] \(\sin(kx + \omega t)\) についても同様にして，波は \(x\) の負の方向へ伝わり，伝播速度 \(v\) は， \[ v = -\frac{\omega}{k}. \]

（３） \(\sin(kx \mp \omega t)\) の \(t\) と \(x\) についての一階微分はそれぞれ， \[ \mp\omega\cos(kx \mp \omega t), \quad k\cos(kx \mp \omega t). \] 二階微分はそれぞれ， \[ -\omega^2\sin(kx \mp \omega t), \quad -k^2\sin(kx \mp \omega t). \] これらを本文，式 (3) の波動方程式 \(\partial^2\phi/\partial t^2 = \alpha^2\ \partial^2\phi/\partial x^2\) の \(\phi\) へ代入すると， \[ -\omega^2\sin(kx \mp \omega t) = -\alpha^2 k^2\sin(kx \mp \omega t). \] 即ち， \[ \alpha^2 = \frac{\omega^2}{k^2}, \] の関係を得ます．また，上の問い（２）の結果から \(\alpha\) が波の速度であることが分かります．

（４） Pa = N/m² = kg m^-1 s^-2 に注意して本文の式 (4) と (5) を計算すると次の結果を得ます． \[ v_P = 5.97\times 10^3\ \mathrm{m/s}, \quad v_S = 3.42\times 10^3\ \mathrm{m/s}. \] 花崗岩のP波とS波の速度はそれぞれ約 6 km/s と 3.4 km/s となりました．なお，地球を構成する岩石の密度 \(\rho\) は深さとともに増加するので， \(v_P\) と \(v_S\) の式は地震波速度は深くなるほど遅くなるような印象を与えます．しかし，実際は弾性定数の \(K\) や \(\mu\) が密度の増加以上に大きくなるので，地震波速度は深さとともに増大します（但し，深さ 100〜200 km のアセノスフェアに相当する低速度層は除きます）．

問題４−２−２ 解答

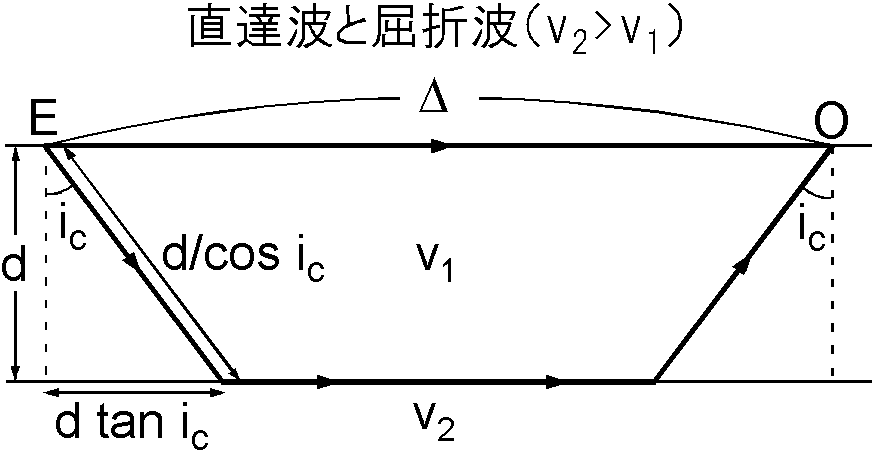
（１） 上図から臨界屈折波が点 O に到達する時間 \(T_3\) は次式で表わされます． \[ T_3 = 2\frac{d/\cos i_c}{v_1} + \frac{\Delta - 2d\tan i_c}{v_2}. \] この式の変形手順はいくつか考えられますが，以下はその一例です． \begin{eqnarray*} T_3 & = & \frac{\Delta}{v_2} + \frac{2d}{\cos i_c}\left(\frac{1}{v_1} - \frac{\sin i_c}{v_2}\right), \\ & = & \frac{\Delta}{v_2} + \frac{2d}{v_1\cos i_c}\left(1 - \frac{v_1}{v_2}\sin i_c\right). \end{eqnarray*} ここで， \(\sin i_c = v_1/v_2\) と \(\cos i_c=\sqrt{v_2^2-v_1^2}\left/v_2\right.\) を代入して， \begin{eqnarray} T_3 & = & \frac{\Delta}{v_2} + \frac{2d}{v_1}\frac{v_2}{\sqrt{v_2^2 - v_1^2}}\frac{v_2^2 - v_1^2}{v_2^2}, \nonumber \\ & = & \frac{\Delta}{v_2} + \frac{2d}{v_1 v_2}\sqrt{v_2^2 - v_1^2}. \label{eq01} \end{eqnarray}

（２） 式 (1) で \(\Delta = \Delta_c\) とした \(T_3\) と 直達波が点 O に到達する時間 \(T_1 = \Delta_c/v_1\) を等置して \(d\) について解きます． \[ \frac{\Delta_c}{v_2} + \frac{2d}{v_1 v_2}\sqrt{v_2^2 - v_1^2} = \frac{\Delta_c}{v_1}, \] \[ \frac{2d}{v_1 v_2}\sqrt{v_2^2 - v_1^2} = \Delta_c\frac{v_2 - v_1}{v_1 v_2}, \] \begin{equation} d = \frac{\Delta_c}{2}\sqrt{\frac{v_2 - v_1}{v_2 + v_1}}. \label{eq02} \end{equation}

（３） P波の地殻とマントルにおける速度 \(v_1\) と \(v_2\) は [km/s] の単位で， \begin{eqnarray*} v_1 & = & 179/31 = 5.77, \\ v_2 & = & (292 - 179)/(45 - 31) = 8.07 \end{eqnarray*} これらの値を式 (2) に代入して，次にように約 36 km です． \[ d = \frac{179}{2}\sqrt{\frac{8.07 - 5.77}{8.07 + 5.77}} = 36.485 \]

問題４−２−３ 解答

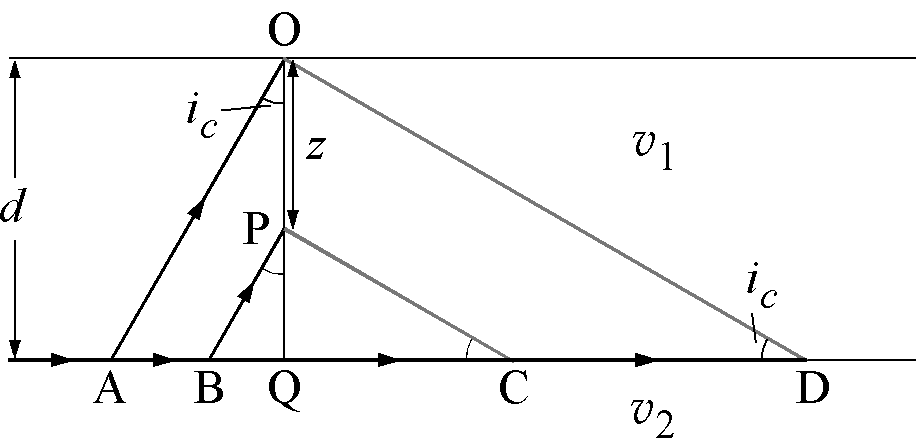
第1層の厚さを \(d\) とすると図より， \begin{eqnarray*} T_1 - T_2 & = & \frac{\overline{AO}}{v_1} - \left(\frac{\overline{AB}}{v_2} + \frac{\overline{BP}}{v_1}\right) = \frac{d}{v_1\cos i_c} - \left(\frac{z\tan i_c}{v_2} + \frac{d-z}{v_1\cos i_c}\right) \\ & = & \frac{z}{v_1\cos i_c} - \frac{z\tan i_c}{v_2}. \end{eqnarray*} ここで， \(\sin i_c = \frac{v_1}{v_2}\) より， \[ \cos i_c = \frac{\sqrt{v_2^2 - v_1^2}}{v_2}, \quad \tan i_c = \frac{v_1}{\sqrt{v_2^2 - v_1^2}} \] を代入して， \begin{eqnarray*} T_1 - T_2 & = & \frac{zv_2}{v_1\sqrt{v_2^2 - v_1^2}} - \frac{zv_1}{v_2\sqrt{v_2^2 - v_1^2}} = \frac{z}{\sqrt{v_2^2 - v_1^2}}\frac{v_2^2 - v_1^2}{v_1v_2} \\ & = & \frac{z\sqrt{v_2^2 - v_1^2}}{v_1v_2}. \end{eqnarray*}

別解：

→ ホーム