問題6−4−1 解答
(1) 本文の式 (8) より, \begin{eqnarray*} (R_X, R_Y, R_Z) & = & (-1.7986, 2.7895, -2.1636), \\ R & = & 3.9620. \end{eqnarray*} 式 (9) より, \[ \tan D_m = 2.7895/(-1.7986), \] の解は -57.187° ですが, \(R_X\) < 0, \(R_Y\) > 0 より, \[ D_m = 180 - 57.187 = 122.813 \approx 122.8°. \] となります.また, \(I_m\) については, \begin{eqnarray*} I_m & = & \sin^{-1}(-2.1636/3.9620), \\ & = & -33.099 \approx -33.1°. \end{eqnarray*} 得られた古地磁気平均方向はサイト(30°N,130°E)としては,地磁気逆転の途中か地磁気エクスカーションのデータと思われます. \(k\) については,式 (10) より, \begin{eqnarray*} k & = & (4-1)/(4-3.9620), \\ & = & 78.947 \approx 78.9. \end{eqnarray*} 式 (11) より, \begin{eqnarray*} \alpha_{95} & = & \cos^{-1}\left(1 - \frac{4-3.9620}{3.9620}\left[20^{1/3} -1\right]\right), \\ & = & \cos^{-1}(0.9836), \\ & = & 10.391 \approx 10.4°. \end{eqnarray*}
(2) 古緯度 \(\lambda\) は \(I_m\) を本文の式 (1) に代入して, \begin{eqnarray*} \lambda & = & \tan^{-1}(\tan(-33.099)/2), \\ & = & -18.053°. \end{eqnarray*} よって,角度 \(p\) は式 (2) より, \begin{eqnarray*} p & = & 90 - (-18.053), \\ & = & 108.053°. \end{eqnarray*} VGP の緯度は式 (3) から, \begin{eqnarray*} \lambda_P & = & \sin^{-1}(\sin 30\times\cos 108.053 + \cos 30\times\sin 108.053\times\cos 122.813), \\ & = & \sin^{-1}(-0.60114), \\ & = & -36.952 \approx -37.0°. \quad (37.0°\mathrm{S}) \end{eqnarray*} 式 (4) の解を \(\beta\) として, \begin{eqnarray*} \beta & = & \sin^{-1}(\sin 108.053\times\sin 122.813/\cos(-36.952)), \\ & = & \sin^{-1}(0.99991), \\ & = & 89.231°. \end{eqnarray*} ここで, \(\cos p\) = -0.3099, \(\sin\lambda_S\sin\lambda_P\) = -0.3006 より, \[ \cos p < \sin\lambda_S\sin\lambda_P, \] ですので, VGP の経度は式 (6) を使用して, \begin{eqnarray*} \phi_P & = & 130 + 180 - 89.231, \\ & = & 220.769 \approx 220.8°. \quad (220.8°\mathrm{E}) \end{eqnarray*}
問題6−4−2 解答
前問「問題6-4-1(1)」の結果は次の通りで,逆転途中または地磁気エクスカーションの方向でした.
- 地点 S の緯度・経度: (30°N, 130°E)
- 古地磁気方向: 伏角 I = -33°, 偏角 D = 123°
- 古緯度 λ = 18°S, 角度 p = 108°
【作図】: 最初に,シュミットネットにトレーシングペーパーを重ね,外周,中心,両極,赤道の両端を写し取ります.
- 経度線は左端を 90°E,中心を 180°E,右端を 270°E と見なして, S をプロットします.さらに, S を極軸の回りに 50° 右方向へ回転し, S' とします(回転1, R1).
- S' を,赤道面内で 90°E と 270°E を結ぶ軸の回りに下方へ 120° 回転して南極点に移し, S'' とします(R2).
- 中心の経度線は S'' から見た北方向ですので,東に偏角 123° の経度線に沿って,角度 \(p\) の 108° 離れた点を VGP の P'' とします.但し,当該の経度線は図の裏側となりますので,点線で表わし, P'' は白丸で表示します.
- トレーシングペーパーはそのままで,シュミットネットを横向きにしてから, S'' と P'' を (b) と逆に回転し(-R2),それぞれ S' と P' とします.その際, S'' は図の表側を移動し, P'' は裏側を移動するので,移動の向きが逆になります. P' は裏側で右端の 270°E のごく近傍に来るはずですので,白丸で表示します.
- シュミットネットを元の縦向きにしてから, S' と P' を (a) と逆に回転し(-R1), S' を S に戻します. P' は僅かに右に移動後に表に現れてから左に移動し,合計で 50° 回転します. P の緯度経度は (37°S, 221°E) と読めます.
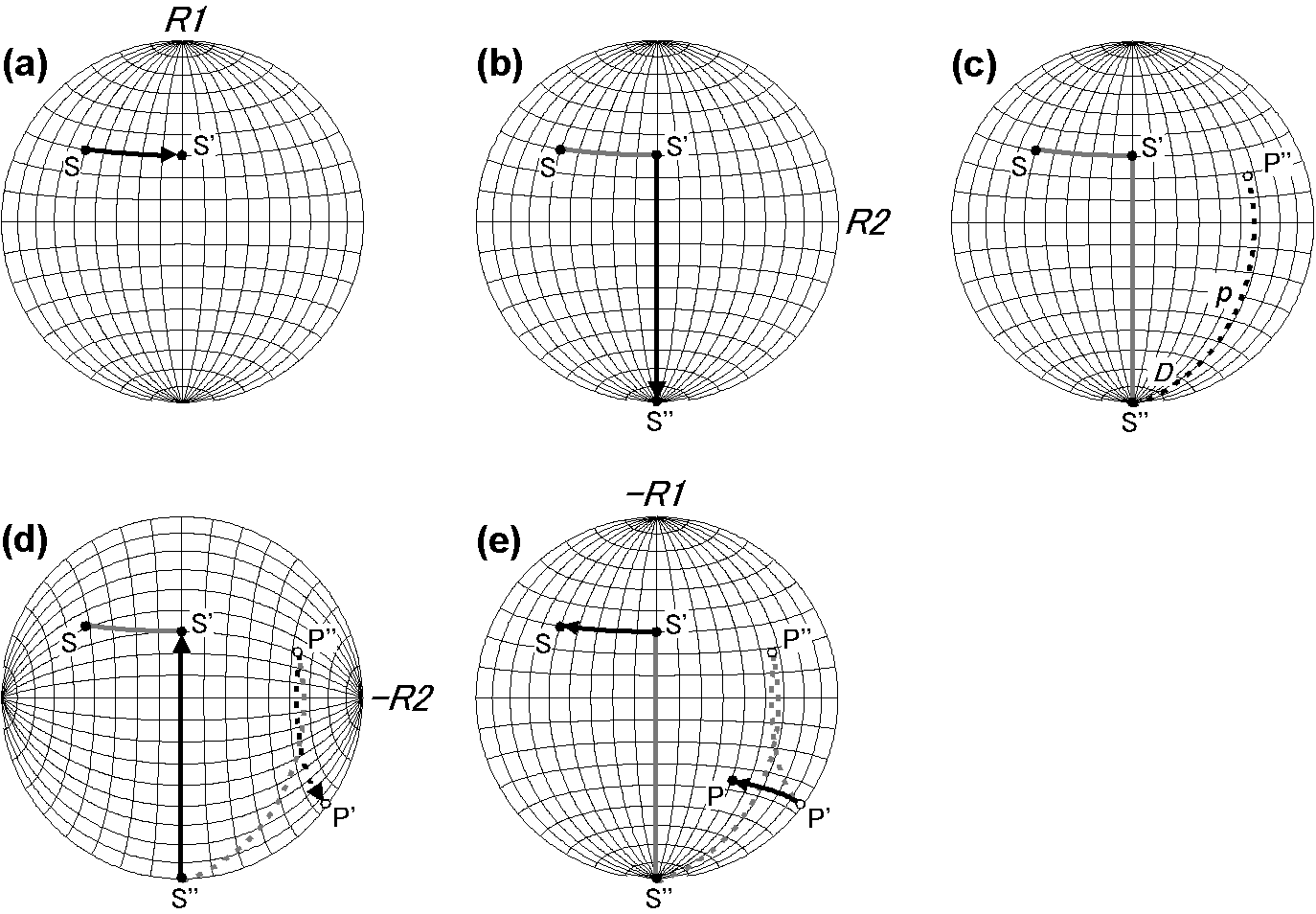
その他の作図法としては,(b) で S' を北極へ移動する方法や,シュミットネットの左端の経度線を 130°E と見なす方法など幾つか考えられますが,ここでは省略します.