問題6-4-1 解説
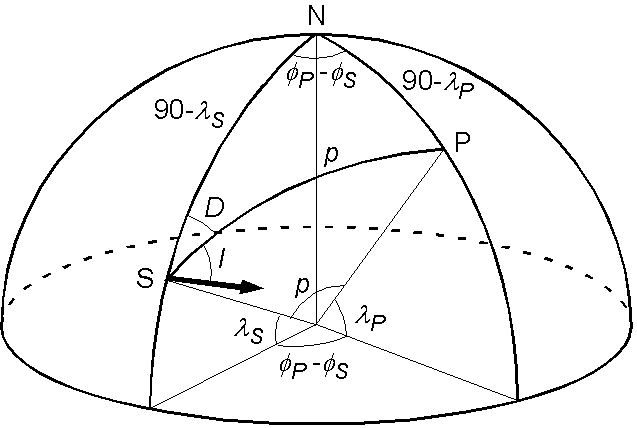
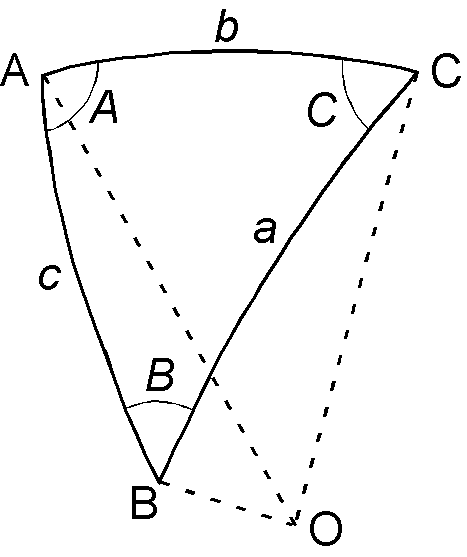
左図の三角形 NSP を右図の三角形 ABC に対応させると,次の形の余弦定理, \[ \cos b = \cos c\cos a + \sin c\sin a\cos B, \] を用いると分かり易いです.すると,偏角 \(D\) を角 \(B\) へ,辺 \(b\) を \(90 - \lambda_P\) へ,などと対応させ, \begin{eqnarray*} \cos(90-\lambda_P) & = & \cos(90-\lambda_S)\cos p + \sin(90-\lambda_S)\sin p\cos D, \\ \sin\lambda_P & = & \sin\lambda_S\cos p + \cos\lambda_S\sin p\cos D, \end{eqnarray*} と,本文の式 (3) を得ます.同様に,正弦定理から, \begin{eqnarray*} \frac{\sin p}{\sin(\phi_P-\phi_S)} & = & \frac{\sin(90-\lambda_P)}{\sin D}, \\ \frac{\sin p}{\sin(\phi_P-\phi_S)} & = & \frac{\cos\lambda_P}{\sin D}, \\ \sin(\phi_P-\phi_S) & = & \frac{\sin p\sin D}{\cos\lambda_P}, \qquad (*) \end{eqnarray*} と,本文の式 (4) を得ます. (*) の \(\phi_P-\phi_S\) の解を \(\beta\) (-90° ≤ \(\beta\) ≤ 90°) とし,図のように \(\phi_P\) が \(\phi_S\) より大きい場合については, \(\phi_P-\phi_S\) が 90° より大きいか小さいかで次のように場合分けする必要があります. \begin{eqnarray*} \phi_P & = & \phi_S + \beta \quad(\mathrm{for}, \ \phi_P-\phi_S\ ≤ 90), \\ \phi_P & = & \phi_S + 180 - \beta \quad(\mathrm{for}, \ \phi_P-\phi_S\ > 90). \end{eqnarray*} その判断のためには,次のように \(\phi_P-\phi_S\) を含む余弦定理を使用して, \begin{eqnarray*} \cos p & = & \cos(90-\lambda_P)\cos(90-\lambda_S) + \sin(90-\lambda_P)\sin(90-\lambda_S)\cos(\phi_P-\phi_S), \\ \cos p & = & \sin\lambda_S\sin\lambda_P + \cos\lambda_S\cos\lambda_P\cos(\phi_P-\phi_S). \end{eqnarray*} この式から, \[ \cos(\phi_P-\phi_S) = \frac{\cos p - \sin\lambda_S\sin\lambda_P}{\cos\lambda_S\cos\lambda_P}, \] となりますが,右辺の分母は常に正なので,次の本文の式 (5) と (6) を得ます. \begin{eqnarray*} \phi_P & = & \phi_S + \beta \quad (\mathrm{for}, \ \cos p ≥ \sin\lambda_S\sin\lambda_P), \\ \phi_P & = & \phi_S + 180° - \beta \quad (\mathrm{for}, \ \cos p < \sin\lambda_S\sin\lambda_P). \end{eqnarray*} また,偏角が西寄りで \(\phi_P\) が \(\phi_S\) より小さい場合は \(\beta\) は負となりますが,この場合も同じ条件式で良いことが分かります.