地心直交座標（x-y-z）と局地座標（n-e-d）の変換行列

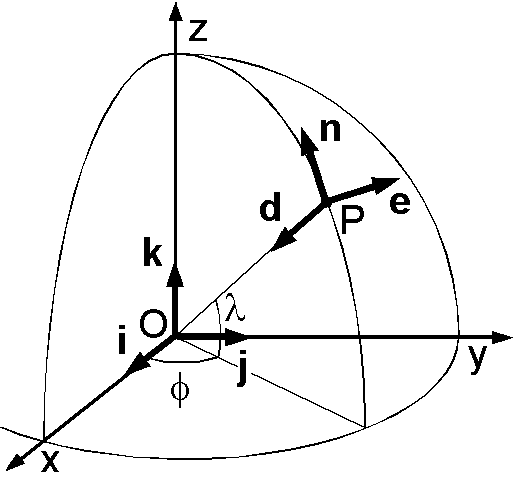
１つのベクトルを異なる２つの直交座標で表すときの座標の変換行列を導きます．原点 O を地球中心とし赤道上で 0°E と 90°E の方向を x と y，自転軸の北極方向を z とした座標系（地心直交座標）を x-y-z 座標とします．また，（緯度，経度）が（\(\lambda\), \(\phi\)）の地点を原点とし北-東-鉛直下を n， e， d 軸とする局地座標系を n-e-d 座標とします．

図のように， x-y-z 座標系の基底ベクトルを \({\bf i}\)， \({\bf j}\)， \({\bf k}\)， n-e-d 座標系の基底ベクトルを \({\bf n}\)， \({\bf e}\)， \({\bf d}\) で表わします．任意のベクトル \({\bf v}\) は次のように２通りに表わすことができます． \[ {\bf v} = v_x{\bf i} + v_y{\bf j} + v_z{\bf k} = v_n{\bf n} + v_e{\bf e} + v_d{\bf d}. \] これより \(v_x\)， \(v_y\)， \(v_z\) は， \begin{eqnarray*} v_x & = & {\bf v}\cdot{\bf i} = v_n{\bf n}\cdot{\bf i} + v_e{\bf e}\cdot{\bf i} + v_d{\bf d}\cdot{\bf i}, \\ v_y & = & {\bf v}\cdot{\bf j} = v_n{\bf n}\cdot{\bf j} + v_e{\bf e}\cdot{\bf j} + v_d{\bf d}\cdot{\bf j}, \\ v_z & = & {\bf v}\cdot{\bf k} = v_n{\bf n}\cdot{\bf k} + v_e{\bf e}\cdot{\bf k} + v_d{\bf d}\cdot{\bf k}, \end{eqnarray*} となるので，次の座標の変換行列を導入します． \begin{equation} A = \left(\begin{array}{ccc} {\bf n}\cdot{\bf i} & {\bf e}\cdot{\bf i} & {\bf d}\cdot{\bf i} \\ {\bf n}\cdot{\bf j} & {\bf e}\cdot{\bf j} & {\bf d}\cdot{\bf j} \\ {\bf n}\cdot{\bf k} & {\bf e}\cdot{\bf k} & {\bf d}\cdot{\bf k} \end{array}\right). \label{eq01} \end{equation} そこで同じベクトルを局地座標で表わしたものを \({\bf v}_L\) とすると，局地座標から地心直交座標への変換は次式となります． \begin{equation} {\bf v} = A {\bf v}_L. \label{eq02} \end{equation} 同様にして， \(v_n\)， \(v_e\)， \(v_d\) は， \begin{eqnarray*} v_n & = & {\bf v}\cdot{\bf n} = v_x{\bf i}\cdot{\bf n} + v_y{\bf j}\cdot{\bf n} + v_z{\bf k}\cdot{\bf n}, \\ v_e & = & {\bf v}\cdot{\bf e} = v_x{\bf i}\cdot{\bf e} + v_y{\bf j}\cdot{\bf e} + v_z{\bf k}\cdot{\bf e}, \\ v_d & = & {\bf v}\cdot{\bf d} = v_x{\bf i}\cdot{\bf d} + v_y{\bf j}\cdot{\bf d} + v_z{\bf k}\cdot{\bf d}, \end{eqnarray*} となり，変換行列は \(A\) の転置行列です． \begin{equation} ^tA = \left(\begin{array}{ccc} {\bf n}\cdot{\bf i} & {\bf n}\cdot{\bf j} & {\bf n}\cdot{\bf k} \\ {\bf e}\cdot{\bf i} & {\bf e}\cdot{\bf j} & {\bf e}\cdot{\bf k} \\ {\bf d}\cdot{\bf i} & {\bf d}\cdot{\bf j} & {\bf d}\cdot{\bf k} \end{array}\right). \label{eq03} \end{equation} よって， \({\bf v}\) の地心直交座標から局地座標への変換は次式となります． \begin{equation} {\bf v}_L = {^t}A {\bf v}. \label{eq04} \end{equation} ここで， \[ {\bf i}=\left(\begin{array}{c}1 \\ 0 \\ 0\end{array}\right), \quad {\bf j}=\left(\begin{array}{c}0 \\ 1 \\ 0\end{array}\right), \quad {\bf k}=\left(\begin{array}{c}0 \\ 0 \\ 1\end{array}\right), \qquad {\bf n}=\left(\begin{array}{c}n_x \\ n_y \\ n_z\end{array}\right), \quad {\bf e}=\left(\begin{array}{c}e_x \\ e_y \\ e_z\end{array}\right), \quad {\bf d}=\left(\begin{array}{c}d_x \\ d_y \\ d_z\end{array}\right), \] を (1) と (3) へ代入すると， \(A\) と \(^tA\) は次のようになります． \begin{eqnarray} A & = & \left(\begin{array}{ccc} n_x & e_x & d_x \\ n_y & e_y & d_y \\ n_z & e_z & d_z \end{array}\right), \label{eq05} \\ ^tA & = & \left(\begin{array}{ccc} n_x & n_y & n_z \\ e_x & e_y & e_z \\ d_x & d_y & d_z \end{array}\right). \label{eq06} \end{eqnarray}

次に，これらの行列の各成分を n-e-d 座標の原点の緯度経度 (\(\lambda\), \(\phi\)) で表わしますが，基底ベクトル \({\bf n}\), \({\bf e}\), \({\bf d}\) の各成分は幾何学を用いて容易に決定できます．例えば，ベクトル \({\bf n}\) は上図のように経度 \(\phi\) の子午面上にあり，z 軸への射影の大きさは \(\cos\lambda\) ですので，\(n_z=\cos\lambda\) となります．また，\({\bf n}\) の x-y 面への射影の大きさは \(\sin\lambda\) で，さらに x 軸と y 軸へ射影し，正負も考慮して，\(n_x=-\sin\lambda\cos\phi\), \(n_y=-\sin\lambda\sin\phi\) となります．\({\bf e}\) と \({\bf d}\) も同様にして，結局 \({\bf n}\), \({\bf e}\), \({\bf d}\) の各成分は次式となります． \begin{equation} \begin{array}{lll} n_x=-\sin\lambda\cos\phi, & n_y=-\sin\lambda\sin\phi, & n_z=\cos\lambda, \\ e_x=-\sin\phi, & e_y=\cos\phi, & e_z=0, \\ d_x=-\cos\lambda\cos\phi, & d_y=-\cos\lambda\sin\phi, & d_z=-\sin\lambda. \end{array} \nonumber \end{equation}

これらを式(5)に代入し，式(2)より \({\bf v}_L\) の局地座標から地心直交座標への変換は， \begin{equation} \left(\begin{array}{c} v_x \\ v_y \\ v_z \end{array}\right) = \left(\begin{array}{ccc} -\sin\lambda\cos\phi & -\sin\phi & -\cos\lambda\cos\phi \\ -\sin\lambda\sin\phi & \cos\phi & -\cos\lambda\sin\phi \\ \cos\lambda & 0 & -\sin\lambda \end{array}\right) \left(\begin{array}{c} v_n \\ v_e \\ v_d \end{array}\right), \label{eq07} \end{equation} となります．同様に式 (6) と式 (4) よりベクトル \({\bf v}\) の地心直交座標から局地座標への変換は次式となります． \begin{equation} \left(\begin{array}{c} v_n \\ v_e \\ v_d \end{array}\right) = \left(\begin{array}{ccc} -\sin\lambda\cos\phi & -\sin\lambda\sin\phi & \cos\lambda \\ -\sin\phi & \cos\phi & 0 \\ -\cos\lambda\cos\phi & -\cos\lambda\sin\phi & -\sin\lambda \end{array}\right) \left(\begin{array}{c} v_x \\ v_y \\ v_z \end{array}\right). \label{eq08} \end{equation}

なお，ベクトル \({\bf n}\), \({\bf e}\), \({\bf d}\) の各成分は以下のようにしても求めることができます．上図から基底ベクトル \({\bf n}\)-\({\bf e}\)-\({\bf d}\) は \({\bf i}\)-\({\bf j}\)-\({\bf k}\) を，(1) y 軸の回りに \(-(90°+\lambda)\) 回転（+yから見て時計回り）してから，(2) z 軸の回りに \(\phi\) 回転（+z から見て反時計回り）すると得られます（原点の平行移動は考慮しません）．回転行列 \(T\) は y 軸と z 軸の回りの回転行列 \(A_y\) と \(A_z\) を利用して次のようになります． \begin{eqnarray*} T & = & \left(\begin{array}{ccc} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{ccc} \cos[-(90°+\lambda)] & 0 & \sin[-(90°+\lambda)] \\ 0 & 1 & 0 \\ -\sin[-(90°+\lambda)] & 0 & \cos[-(90°+\lambda)] \end{array}\right), \\ & = & \left(\begin{array}{ccc} -\sin\lambda\cos\phi & -\sin\phi & -\cos\lambda\cos\phi \\ -\sin\lambda\sin\phi & \cos\phi & -\cos\lambda\sin\phi \\ \cos\lambda & 0 & -\sin\lambda \end{array}\right). \end{eqnarray*} 回転行列の公式によると（ → このページの式 (6)），この回転行列 \(T\) の第1列，第2列，第3列はそれぞれ基底ベクトル \({\bf n}\), \({\bf e}\), \({\bf d}\) となります．結局，この回転行列 \(T\) は式 (5) の \(A\) を表わします．

→ ホーム