問題7-3-1 解説
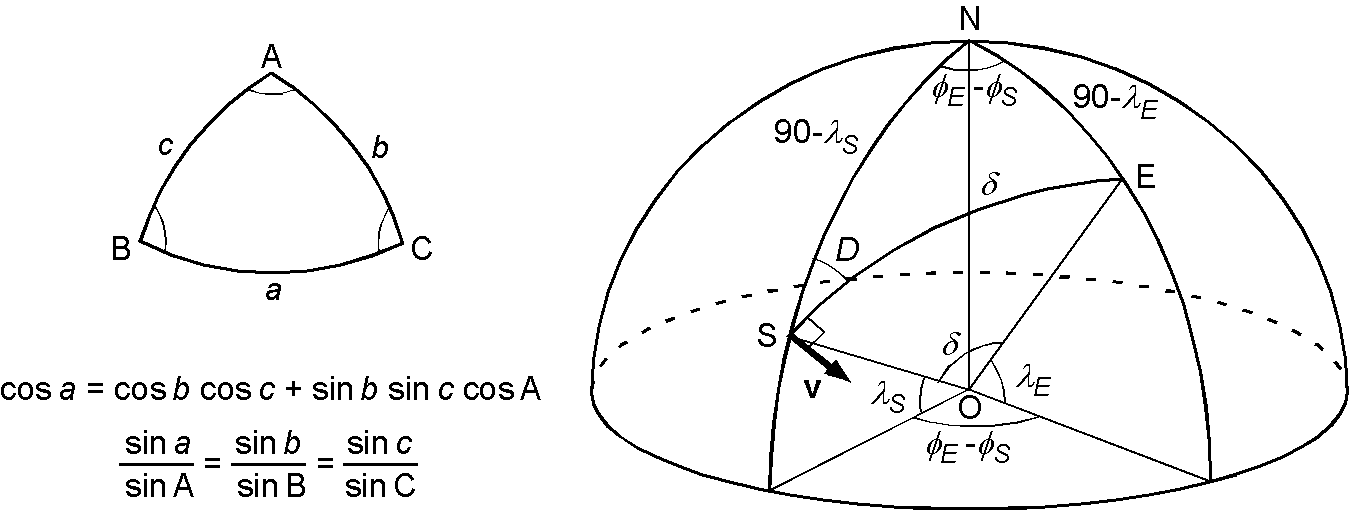
(1) 図(左)と(右)の球面三角形の対応を, A→N, B→S, C→E とすると,余弦定理からは, \begin{eqnarray*} \cos\delta & = & \cos(90-\lambda_E)\cos(90-\lambda_S) + \sin(90-\lambda_E)\sin(90-\lambda_S)\cos(\phi_E-\phi_S), \\ & = & \sin\lambda_E\sin\lambda_S + \cos\lambda_E\cos\lambda_S\cos(\phi_E-\phi_S). \end{eqnarray*} 正弦定理からは, \begin{eqnarray*} \frac{\sin\delta}{\sin(\phi_E-\phi_S)} & = & \frac{\sin(90-\lambda_E)}{\sin D}, \\ \sin D & = & \frac{\cos\lambda_E\sin(\phi_E-\phi_S)}{\sin\delta}. \end{eqnarray*}
(2) これらの式に数値を代入して, \[ \cos\delta = \sin 62.4\sin65 + \cos 62.4\cos65\cos(135.8+20) = 0.6246 \] これより, \(\delta\) = 51.35 となります.この値を使って \(D\) は, \[ \sin D = \cos 62.4\sin 155.8/\sin 51.35 = 0.2432 \] より, \(D\) = 14.07 となります.回転運動の角速度をラジアンに直すと, \begin{eqnarray*} \omega & = & 0.21\ \mathrm{°/Myr}, \\ & = & \left(0.21\times\frac{3.14}{180}\right)\times\frac{1}{10^6}, \\ & = & 3.663\times 10^{-9}\ \mathrm{rad/yr}. \end{eqnarray*} アイスランドでの,北米プレートに対するユーラシアプレートの相対速度は本文の式 (11) から, \begin{eqnarray*} v & = & (3.663\times 10^{-9})\times(6400\times 10^5)\times\sin(51.35), \\ & = & 1.83\ \mathrm{cm/yr}. \end{eqnarray*} 以上より,相対速度の大きさは約 1.8 cm/yr で,速度ベクトルの方向は \(D\) に 90° を加えて,北から東回りに 104° となります.
大西洋中央海嶺はアイスランドでは地上に現れています.中央海嶺の拡大速度は両側拡大速度を指すことが多いようで,その場合は上の値で良いですが,片側拡大速度の場合は上の値を2で割って 0.9 cm/yr となります.また,中央海嶺におけるプレートの拡大方向については,ユーラシアプレートに対する北米プレートの速度方向,北から西回りに 76°,についても言及する必要があるでしょう.
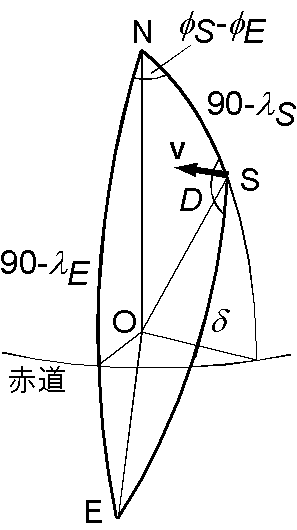
(3) \(\lambda_E\) や \(\phi_E-\phi_S\) が負になりますが,上の式にそのまま代入すれば解が得られます(但し,逆正弦関数の角度の任意性には注意が必要です).しかし,ここでは右図の角度 \(D\) が鈍角の球面三角形に直接公式を当てはめてみます. \begin{eqnarray*} \cos\delta & = & \cos(90-38)\cos(90+61.1) \\ & & + \sin(90-38)\sin(90+61.1)\cos(142-94.2), \\ & = & -0.2832 \end{eqnarray*} これより, \(\delta\) = 106.45 となります.この値を使って \(D\) は, \[ \sin D = \sin 151.1\sin 47.8/\sin 106.45 = 0.3733 \] より, \(D\) = 21.92 ですが,正しい値はこの補角ですので, \(D\) = 158.08 となります.速度ベクトル \({\bf v}\) の方向はこの角度から 90° 引いて,西回りに 68.08° となります.角速度については,ラジアンに直すと, \[ \omega = 0.86\times(3.14/180)/10^6 = 1.500\times 10^{-8}\ \mathrm{rad/yr}. \] よって,東北沖におけるユーラシアプレートに対する太平洋プレートの相対速度の大きさは, \[ v = (1.500\times 10^{-8})\times(6400\times 10^5)\times\sin(106.45) = 9.21\ \mathrm{cm/yr}. \] 以上より,東北付近での太平洋プレートの運動は北から西に 68° で年間 9.2 cm の速度となり,問い (2) で求めた大西洋中央海嶺のアイスランド付近での拡大速度より格段に大きいことが分かります.
別解:
与えられたオイラー極 (61.1°S, 94.2°E) の対極 (61.1°N, 274.2°E) をオイラー極として,太平洋プレートに対するユーラシアプレートの回転運動を求めます.すると問い (1) の図と同じ設定で, \(\delta\) は 73.55°, \(D\) は 21.92° となり,当然 \(v\) は同じ値を得ます.よって,東北付近での太平洋プレートに対するユーラシアプレートの運動は北から東に 112° で年間 9.2 cm との表現となりますが,日本列島を主体に考える立場からは違和感があります.実際,ホットスポットを基準とした絶対運動モデルでは(HS3-NUVEL-1A, Gripp & Gordon 2002),太平洋プレートの角速度はユーラシアプレートの約5倍大きいようです.また,プレートの平均回転をゼロとする平均リソスフェアモデルでは(NNR-NUVEL-1A, Argus & Gordon 1991)3倍程度となっています.