問題1-3-2 解説
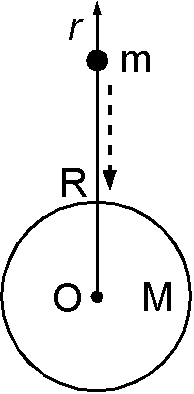
(1) 万有引力に抗する力は, \(GMm/r^2\) ですので,これを \(r=R\) から \(r=\infty\) まで積分して, \begin{eqnarray*} U & = & \int_R^\infty \frac{GMm}{r^2} dr, \\ & = & \left[-\frac{GMm}{r}\right]_R^\infty, \\ & = & GMm\left(-\frac{1}{\infty} + \frac{1}{R}\right), \\ & = & \frac{GMm}{R}. \end{eqnarray*}
(2) 重力エネルギーを運動エネルギーと等しいとおいて, \begin{eqnarray*} \frac{1}{2}mv^2 & = & \frac{GMm}{R}, \\ v & = & \sqrt{\frac{2GM}{R}}. \end{eqnarray*}
(3) \(M\) を計算すると, \[ M = \frac{4\pi\times(2000\times 10^3)^3\times 5000}{3} = 1.6755\times 10^{23}\ \mathrm{kg}. \] \(U\) は (1) から, \begin{eqnarray*} U & = & \frac{(6.674\times 10^{-11}\ \mathrm{m^3\,kg^{-1}\,s^{-2}})\times(1.6755\times 10^{23}\ \mathrm{kg})\times(1\ \mathrm{kg})}{2\times 10^6\ \mathrm{m}},\\ & = & \frac{1.1182\times 10^{13}}{2\times 10^6}\ \mathrm{kg\,m^2\,s^{-2}},\\ & = & 5.591\times 10^6\ \mathrm{J}. \end{eqnarray*} \(v\) は (2) から, \begin{eqnarray*} v & = & \sqrt{\frac{2\times(6.674\times 10^{-11}\ \mathrm{m^3\,kg^{-1}\,s^{-2}})\times(1.6755\times 10^{23}\ \mathrm{kg})}{2\times 10^6\ \mathrm{m}}},\\ & = & 3.34\times 10^3\ \mathrm{m/s}. \end{eqnarray*} 秒速約 3 km となります.
(4) 温度の上昇 \(\Delta T\) は,求めたエネルギー \(U\) を物体の熱容量(質量\(\times\)比熱)で割って, \begin{eqnarray*} \Delta T & = & \frac{5.591\times 10^{6}\ \mathrm{J}}{(1\ \mathrm{kg})\times(1000\ \mathrm{J\,kg^{-1}\,K^{-1}})},\\ & = & 5590\ \mathrm{K}. \end{eqnarray*}
補足:天体スケールの力学的エネルギー保存則
本文の式 (3) で表わされる力学的エネルギー保存則は重力加速度が一定と見なせる地表付近で適用されます.この問題のような天体スケールでは,引力が万有引力の法則に従い距離に依存します.天体スケールのエネルギー保存則は → このページで解説しています.