問題1-2-3 解説
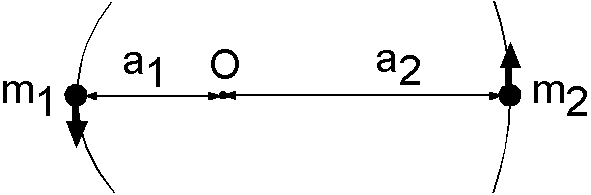
主星については,重心 O の回りの半径 \(a_1\) の円運動による向心力と,距離が \(a=a_1+a_2\) 離れた伴星との間に働く万有引力を等しいとおき, \[ m_1 a_1 \omega^2 = G\frac{m_1 m_2}{a^2}. \] この式から \(m_1\) を消去して整理すると, \[ a_1 a^2\omega^2 = G m_2. \] 伴星についても同様にして, \[ a_2 a^2\omega^2 = G m_1. \] これらの式を足し合わせて, \[ (a_1 + a_2)a^2\omega^2 = G(m_2 + m_1). \] これに, \(a=a_1+a_2\) と \(\omega = 2\pi/T\) を代入して整理すると,次の一般化されたケプラーの第3法則となります. \[ \frac{a^3}{T^2} = \frac{G}{4 \pi^2} (m_1 + m_2). \]
おおいぬ座の恒星シリウスは連星で,周期は約 50 年,両星間の平均距離は約 20 au(天文単位)です.軌道は楕円ですが,円軌道と仮定して,上で得た式を適用して両星の質量の和を求めてみます.
- \(G\) = 6.674\(\times\)10\(^{-11}\) m\(^3\) kg\(^{-1}\) s\(^{-2}\)
- \(a\) = 20\(\times\)1.496\(\times\)10\(^{11}\) = 2.992\(\times\)10\(^{12}\) m
- \(T\) = 50\(\times\)365.26\(\times\)24\(\times\)3600 = 1.578\(\times\)10\(^9\) s
を代入して計算すると, \[ m_1 + m_2 = 6.36\times 10^{30}\ \mathrm{kg}, \] となり,太陽質量の約3倍です.
一方, \(a_1\) と \(a_2\) の値,または比が分かれば, O は重心ですので, \[ \frac{m_1}{m_2} = \frac{a_2}{a_1}, \] の関係を利用して \(m_1\) と \(m_2\) を個別に求めることができます.そこで, \[ a_1 : a_2 = 1 : 2, \] と仮定すると,主星は太陽質量の約2倍,伴星はほぼ同じとなります.実測値は Wikipedia によると,質量の和は 5.96\(\times\)10\(^{30}\) kg,主星と伴星はそれぞれ太陽質量の 2.02 倍,0.978 倍となっています.