問題1−1−1 解答
\(T^2 = k a^3\) (\(k\)は比例定数) ならば, \[ \log_{10}T = {\scriptsize \frac{1}{2}}\log_{10}k + {\scriptsize \frac{3}{2}}\log_{10}a. \] よって,両対数グラフに \(a\) と \(T\) を直接プロットすれば,傾きが 3/2 の直線になり,結果は下図の通りです.グラフの傾きは定規や分度器などで直接確認できます.
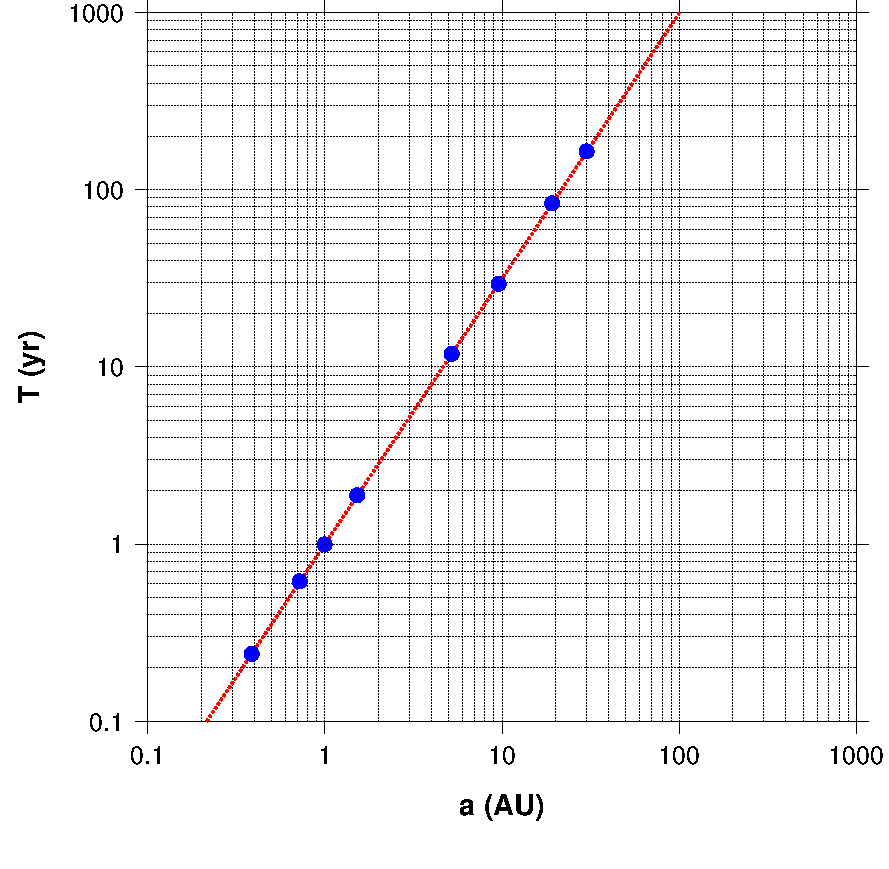
問題1−1−2 解答
\(a_n = a_0 p^n\) ならば,次式が成り立ちます. \[ \log_{10}a_n = \log_{10}a_0 + n\log_{10}p. \] 従って,片対数グラフに \(n\) を横軸,\(a_n\) を縦軸に取りデータをプロットすれば,直線に並ぶはずです.結果は下図の通りで,左がケレスを除外した場合,右が含めた場合です.
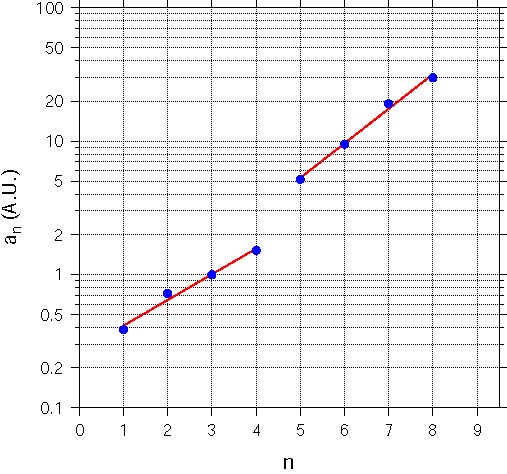
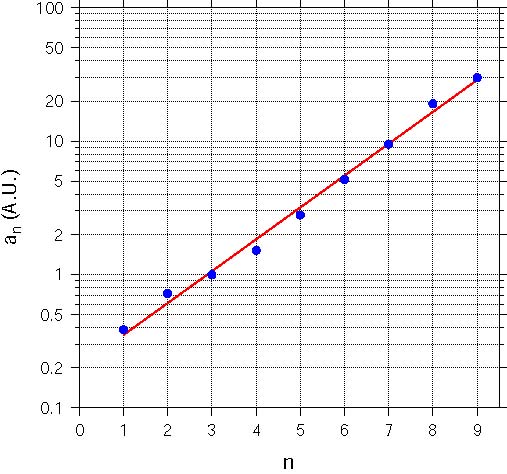
ケレスを含めた右のグラフの方がデータの直線性は良いように見えますが,左の図も1本の直線で近似して比較するべきでしょう.
問題1−1−3 解答
座標軸を下図のように取ります.
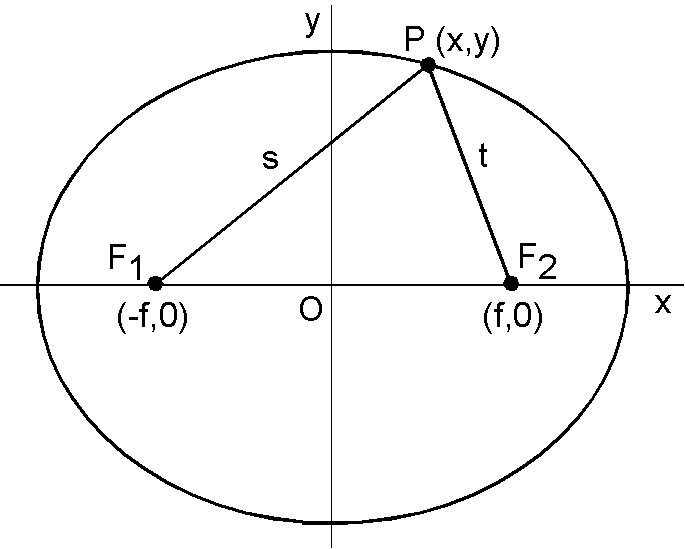
(1) 条件の \(s+t=2a\), \[ \sqrt{(x+f)^2 + y^2} + \sqrt{(x-f)^2 + y^2} = 2a. \] を2回2乗して変形すると楕円の方程式となります.まず,左辺の第2項を右辺に移行してから2乗するのがコツです.
(2) \(s+t\) は一定の 2\(a\) ですので,その平均 \(\overline{s+t}\) も一定値の 2\(a\) です.一方, \(s\) と \(t\) は全く反対称に変化しますので,その平均値は等しく, \(\overline{s+t}\) の 1/2 となります.よって, \[ \overline{s} = \overline{t} = (\overline{s+t})/2 = a. \] 別解としては,\(s\) を \(x\) の式で表すよう上記の式を変形すると, \[ s = \frac{f}{a}x + a. \] となります.よって, \(s\) は \(x\) の1次式で変化し,その平均は最小値と最大値の平均に等しくなるので, \[ \overline{s} = \frac{(a-f) + (a+f)}{2} = a. \]