問題3-5-3 解説
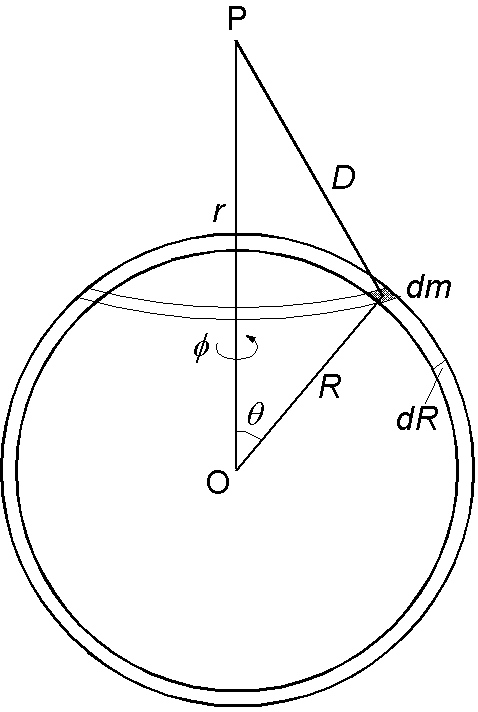
\(dV=-\frac{G}{D}dm\) を \(\phi\) は 0 から 2π, \(\theta\) は 0 から π, \(R\) は 0 から \(a\) まで積分します. \begin{eqnarray*} V & = & \int_0^a dR\int_0^\pi d\theta\int_0^{2\pi}-\frac{G}{D}\rho R^2\sin\theta d\phi, \\ & = & -2\pi\rho G\int_0^a dR\int_0^\pi R^2\frac{\sin\theta}{D}d\theta. \end{eqnarray*} ここで, \(D=\sqrt{r^2 + R^2 - 2rR\cos\theta}\) を \(\theta\) で微分すると, \[ dD = \frac{rR\sin\theta}{\sqrt{r^2 + R^2 - 2rR\cos\theta}}d\theta = rR\frac{\sin\theta}{D}d\theta, \] 即ち, \[ \frac{\sin\theta}{D}d\theta = \frac{1}{rR}dD, \] の関係を使用して,積分変数を \(\theta\) から \(D\) へ変換します. \begin{eqnarray*} V & = & -\frac{2\pi\rho G}{r}\int_0^a RdR\int_{r-R}^{r+R}dD, \\ & = & -\frac{2\pi\rho G}{r}\int_0^a RdR[r+R-r+R], \\ & = & -\frac{4\pi\rho G}{r}\int_0^a R^2dR, \\ & = & -\frac{4\pi\rho G}{r}\frac{a^3}{3} = -\frac{GM}{r}. \end{eqnarray*} 得られた \(V\) は \(r\) だけの関数ですので,点 P における球の引力による加速度 \(g\) は, \[ g = -\frac{dV}{dr} = -\frac{d}{dr}\left(-\frac{GM}{r}\right) = -\frac{GM}{r^2}. \] 負の記号は加速度が \(-r\) の方向,球の中心を向いていることを示します.
補足:球殻の内部の点のポテンシャルは一定となることについて
球殻の内部の点(球殻で囲まれた空間に位置する点)には力が働かないこともポテンシャルを用いると式が簡単になります.厚さ \(dR\) の球殻の内部の点 P のポテンシャルは,上記で \(R\) で積分する前の式を \(D\) について \(R-r\) から \(R+r\) まで積分することで得られます. \begin{eqnarray*} dV & = & -\frac{2\pi\rho G}{r}R\int_{R-r}^{R+r} dD, \\ & = & -\frac{2\pi\rho G}{r}R[R+r-R+r], \\ & = & -4\pi\rho GR. \end{eqnarray*} これは \(r\) に依存しない一定値ですので,球殻の内部の点 P には力は働きません.例えば,厚さ \((b-a)\) の球殻で囲まれた空間内の任意の点のポテンシャルは,これを \(R\) で積分して, \[ V = -4\pi\rho G\int_a^b R dR = -2\pi\rho G(b^2-a^2), \] となり, \(-\nabla V=0\) となります.