問題6−1−1 解答
(1) 伏角 \(I\),偏角 \(D\),全磁力 \(F\) の定義式(本文の式 (1))と \(Y\) = 0 より, \begin{eqnarray*} \tan I & = & \frac{Z}{X} = \frac{\mu_0 M\sin\lambda}{2\pi a^3}\times\frac{4\pi a^3}{\mu_0 M\cos\lambda}, \\ & = & 2\tan\lambda, \\ D & = & 0, \\ F & = & \sqrt{X^2 + Z^2} = \frac{\mu_0 M}{4\pi a^3}\sqrt{\cos^2\lambda + 4\sin^2\lambda} = \frac{\mu_0 M}{4\pi a^3}\sqrt{1 + 3\sin^2\lambda}, \\ & = & F_0\sqrt{1 + 3\sin^2\lambda}. \end{eqnarray*} ここで, \[ F_0 = \frac{\mu_0 M}{4\pi a^3}, \] は,赤道(\(\lambda\) = 0)での全磁力です.\(F_0\) = 30 μT と仮定すると,磁気双極子モーメントは \(M = 7.9\times 10^{22}\ \mathrm{Am^2}\) となります.
(2) 次の図のようになります.
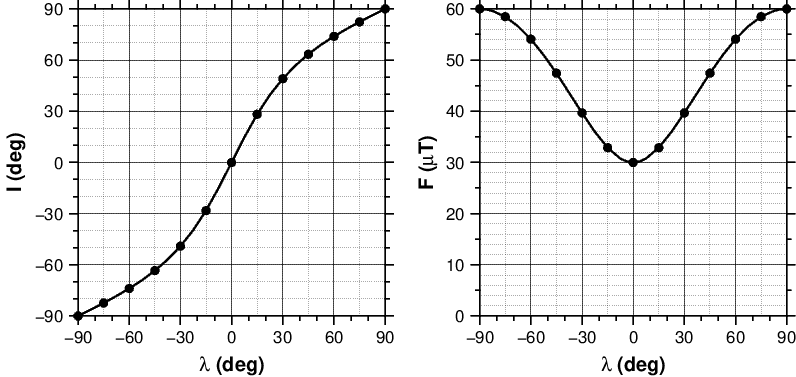
(3) 伏角については赤道域でほぼ水平(0°)で,緯度とともに深くなり両極域でほぼ 90° となります.また,伏角は北半球では下向き(正)で,南半球では上向き(負)です.偏角と全磁力については伏角ほど分かり易くないですが,よく観察すれば次のことが言えます.偏角は赤道域と中緯度地域ではほぼ北向き(0°)です.全磁力は大雑把に見れば赤道域で小さく,緯度とともに増加します.また,全磁力は赤道域ではほぼ 30 μT で,極域ではその2倍の約 60 μT です.
問題6−1−2 解答
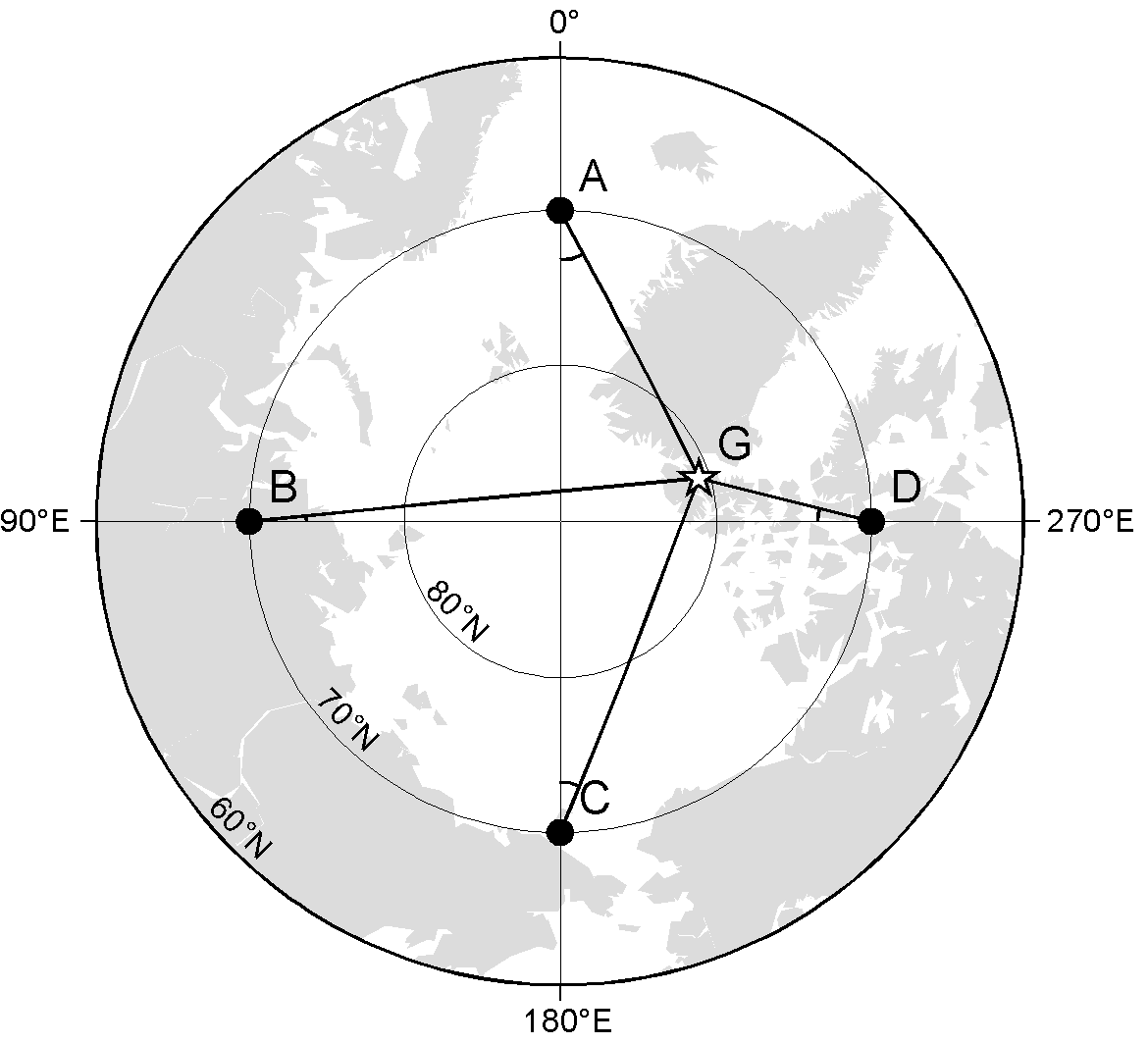
観測点の緯度として通常の地理緯度ではなく,磁極を基準とした磁気緯度を考え \(\lambda\) とし,その余角(余緯度)を \(\theta=90-\lambda\) とします.観測点における伏角 \(I\) は \(\lambda\) や \(\theta\) を用いて次のように表わせます. \[ \tan I = 2\tan\lambda = \frac{2}{\tan\theta}. \] 図で磁極 G と各観測点を結ぶ線は直線ではなく大円の一部で,その曲線に沿った角距離が \(\theta\) です.上の2番目の式から \(\theta\) が小さいほど,即ち曲線の長さが短いほど観測点における \(I\) は大きくなります.また,観測点における偏角は,曲線と観測点を通る経線とのなす角度です.以上の2点を考慮して図を観察することで下表の結果が得られます.
| 測定番号 | 伏角(°) | 偏角(°) | 地点記号 |
|---|---|---|---|
| 測定値1 | 84 | 13 | D |
| 測定値2 | 80 | -27 | A |
| 測定値3 | 77 | 21 | C |
| 測定値4 | 75 | -5 | B |
なお,上の結果は単純な双極子磁場による地磁気のモデルに対するものですので,実際の地磁気でもこの通り観測されるとは限りません.実際の地磁気は非双極子磁場も多く含み,特に極域ではこのモデルからのずれは大きくなります.