| トップページへ | 研究指針の目次 |
目次
215.1 私の研究観
215.2 はじめに
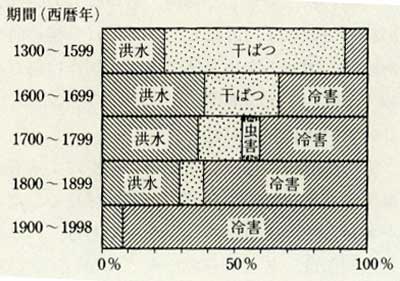
日本の途上国から先進国への道程ー災害克服の歴史
私の少年時代
私の大学~院生時代
極小低温層の研究
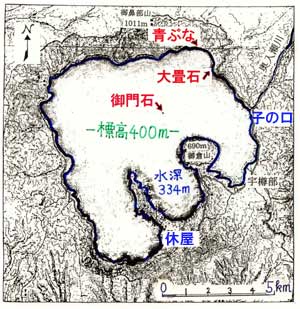
215.3 十和田湖物語ー戦後復興と電力不足
215.4 海面バルク法物語ー数値予報精度向上の「気団変質実験」
海面バルク法の精度向上
KEYPSの式の確認研究
カルマン定数
215.5 熱・水収支の研究
森林蒸発散と砂漠気候
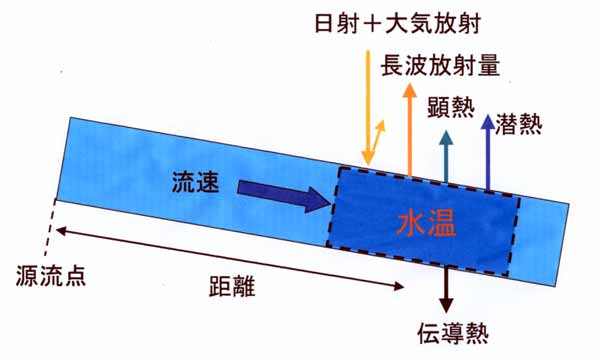
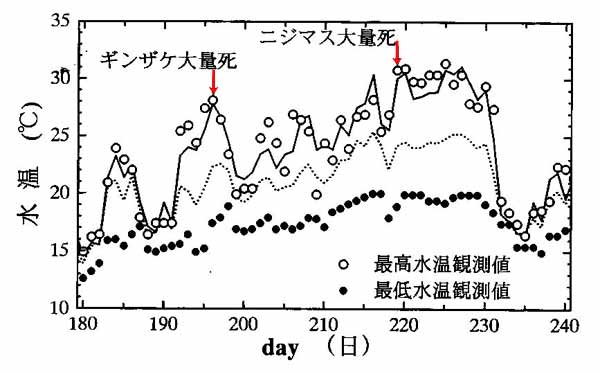
河川水温の研究
215.6 地球温暖化量の正しい評価(定年後の仕事)
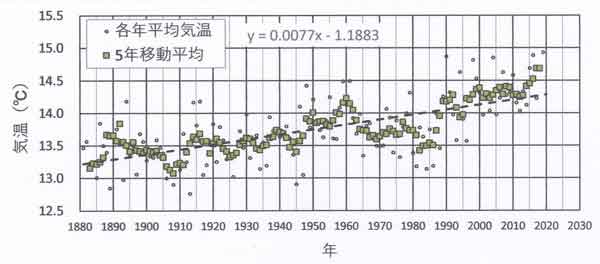
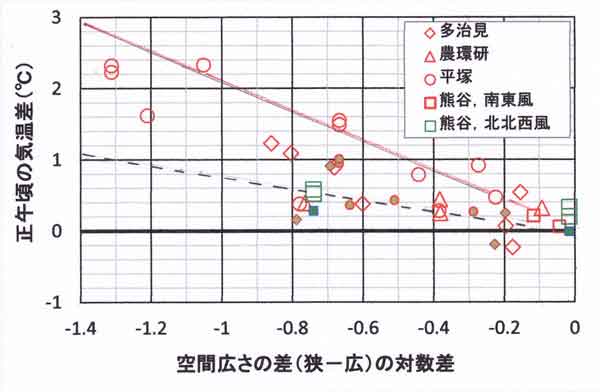
日だまり効果
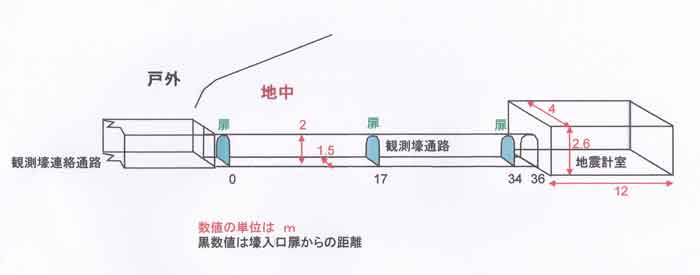
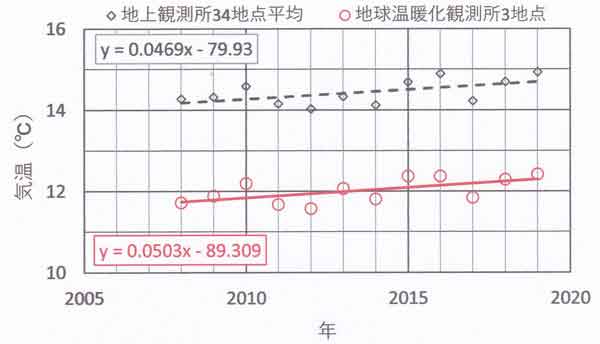
地中温度から地球温暖化量を知る
「地球温暖化観測所」設立の提案
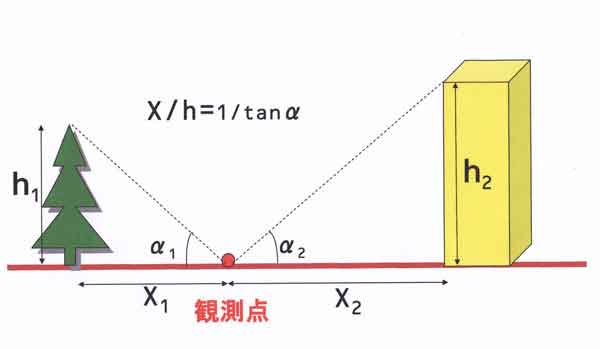
付録(1)樹木の風下における気温上昇の実測
付録(2)「地球温暖化観測所」設置の要請書(中央電気倶楽部)
文献


|
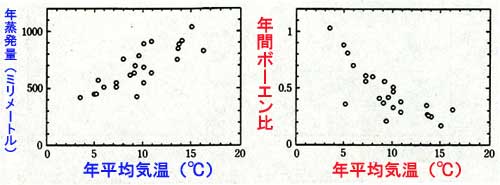
「キンク」(遷移層)の存在を否定する研究 最初に、「キンク」は風速計の動特性から生じる誤差ではないかと疑い、理論的に 誤差であることを示した(Kondo et al. 1971)。さらに観測によって確かめる 必要があり、独特な観測方法でキンクの存在を否定することができた。 特殊な方法とは、軽量で追従性のよい3個の風速計を一体支柱に下端から0.0m、0.6m、 1.8mの位置に固定する。他の1個は高度6mに設置しておく。一体支柱を上下に動か せば、例えば海面上の0.3m、0.9m、2.1m、6mの風速を測れる。続いて、一体支柱を 上げて、4.0m、4.6m、5.8m、6mの風速を測れば、この高度範囲では風速鉛直勾配 が小さいので風速計相互の器差が狂っていないかチェックできる。この方法を繰り 返せば海面上の風速の鉛直分布を正確に測ることができる。 こうした一連の観測で予期せぬ大きな副産物も得られた。風向と波の方向が 一致するときと反対のときで、海面波に誘起された風速変動の位相差が180度変わる ことがわかった(Kondo et al.1972)。 それは、海面上の風速鉛直分布を測るために、風速計が波で壊れてもよい覚悟で 取り付けてあった。台風による「うねり」が強くなり風速計が壊れていないか、 夜になって心配になり陸上で記録していた風速計の電磁カウンターを見に行くと、 カウンターのカチカチ音が「うねり」の周期と同じ約12秒の周期で変動するのが聞 こえたのである。 そうして、いろいろな条件について海面波と風速変動の関係を 明らかにすることができたのである。 |
|
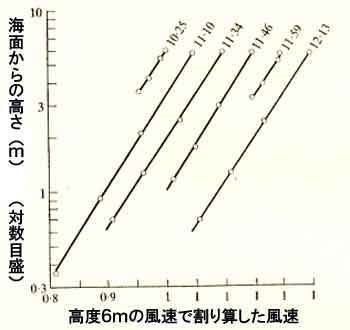
準備研究と追試研究 (1)準備研究 (1-1) 当時の風杯式風速計は風杯の大きさに比べて回転半径が大きい 小型の3杯式風速計が使われていた。この風速計の動特性(レスポンス)から乱流内で は平均風速が強めに観測される。1960年以前に気象庁で使われていた4杯式ロビンソン 風速計も乱流状態にある大気境界層内の風速は10~20%ほど強く観測される。 私はレスポンスのよい風速計が必要と考え、独自に開発した光の透過・遮蔽で回転数 を測る軽量の3杯式微風速計を1960年から使っていた。 (1-2) 観測塔に風速計をとりつけたいのだが、塔自体が自然風を乱すので、 測器を塔からどれだけ離せばよいかの検討を行った。観測塔の周りでの観測と模型に よる観測をおこなった。非粘性流体を仮定したときのポテンシャル流が塔の前方 から直角横方向の範囲までよい近似で表わされることもわかった (Kondo and Naito, 1972)。これらを参考にして測器取り付け位置を決めることが できた。 (2)追試研究 (2-1)大気安定度を考慮したバルク法ができた(Kondo, 1975)。 それを用いて東シナ海の大気・海面間の顕熱・潜熱交換量を評価した。 冬の東シナ海では莫大なエネルギーが黒潮から大気へ供給されて、気団変質が 行われている。世界でもっとも激しいエネルギー交換の場所であることがわかった。 AMTEX観測では、東シナ海の大気柱の熱・水収支量をラジオゾンデのデータから 計算する「大気水収支法」による計算も行われた(Nitta, 1976)。両者はよく 一致した(Kondo, 1976)。それゆえ、バルク法は完成したことになる。 (2-2)バルク法が精度よく海面熱収支量を評価できることについて、世界中で 行われた超音波風速計による海面熱・水収支量の渦相関法の観測から得られたバルク 係数と比較し、両者は矛盾なく一致していることを確認した(Kondo, 1977)。 (2-3)特に、大気安定度が不安定な微風時について渦相関法によって求められた Bradley et al(1991)の交換速度(=バルク係数×風速)とも比較し、両者は よく合っていることを確認した(Kondo and Ishida,1997)。 (2-4)海面が強風になるにしたがって、なぜ「空気力学的に粗な面」になるかを明ら かにしなければならない。微風のときは空気力学的に「滑らかな面」であるが、 「粗な面」になるのは、うねりや有義波高のような長周期波がつくる凹凸ではなく、 風波が砕ける高周波の砕波(波しぶきのもと)によることを示すために、3~40ヘルツ の範囲の高周波成分が測れるエナメル被覆の細い銅線で作った電気容量式波高計を つくり、高周波成分の大きさが風速と密接に関係している、つまり「空気力学的粗度」 と「高周波成分の幾何学的粗度」が密接に関係していることを示した (Kondo et al. 1973)。 われわれは強風時の海面を遠方から眺めて白波一面と感じるのだが、塔の上から見ると (写真撮影すると)その面積割合は意外に少ない。白波として認識される幾何学的 粗度は高周波成分の一部分であることがわかった。 |
|
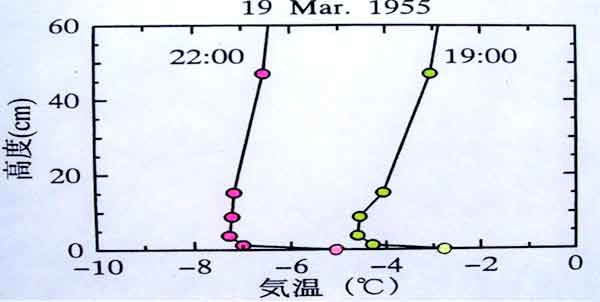
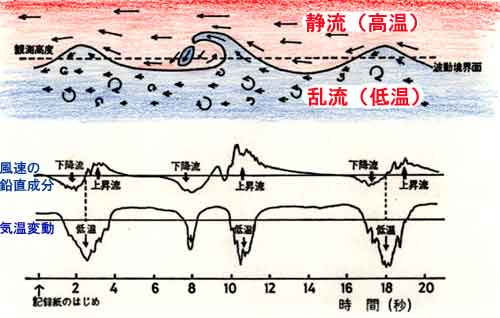
間欠乱流を確認する行動 観測時の夜半に乱流変動のモニター(ペン書き記録計)を見ていると、風速と 気温変動がピタリと止まることがある。記録計の変動幅フルスケールを越えた温度 なのか、実際に乱流が無くなったのか不明である。これまでは、高度数mで乱流変動 がなくなるということを論文で見たことはなかった。 念のために、うちわを持って観測塔に登り、超音波風速計の下から扇ぐと風速鉛直 成分のモニター記録計のペン先は上向き振れる。息を吹きかけると、気温変動成分の モニター記録計のペン先は高温側に振れた。 こうした結果、「本当に乱流が止まり”静流”状態になったのだ!」とモニターの 記録が真の変動を示していることを確認した。 すなわち、静流が続き、間欠的に乱流が起きていることを発見した。地表面に 近い層ではいつでも乱流であるが、非常に安定になると高度数mから上では乱流は なくなることがわかったのである。安定度を表すリチャードソン数(Ri)は、 安定時には、高度とともに大きくなり、0.2<Ri<2で間欠乱流が生じ、 2<Ri で静流となる。 図に示した模式図から理解されるように、静流状態が近づくと、乱流層と静流層の 境界面は波を打つかのように流れている。下層の低温気塊は波によって砕けて 落下しても、顕熱を運んだことにならず、上下に波打っただけである。そのために、 それらの層の間で運動量は上から下に輸送されても、顕熱はほとんど輸送されない。 それはこういうことだ。つまり、下層の風速の小さい気塊が持ち上がり、上層で 加速されたのち、下層に戻ってくると周囲から減速作用を受ける。これは運動量 が上から下へ輸送されたことになる。いっぽう、下層の低温気塊が持ち上がり、 上で混合されることなく、再び下層に落下してきても、波を打っただけで顕熱は 伝えたことにならないからである。 |
|
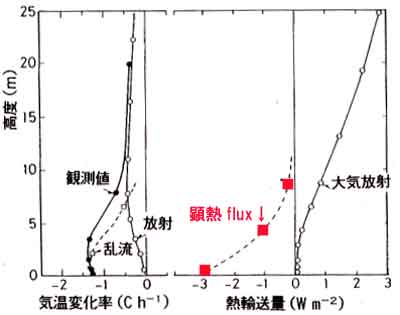
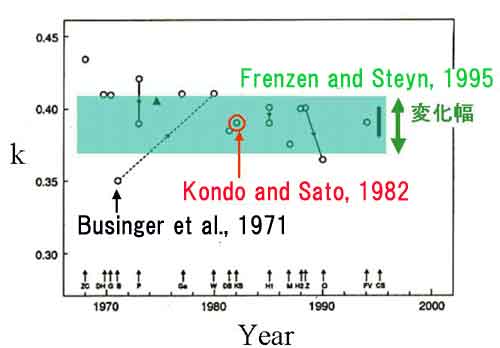
k=0.35を唱える世界の雰囲気を打ち払うべし k=0.35を信じる世界の雰囲気を打ち払うべきだと考えた。正確なカルマン定数を 求めるには、普通の方法・態度で観測してもだめ、特別な工夫・注意が必要である。 4年間にわたり観測した。大気安定度が中立で、高度20m以下の接地境界層内の 風速鉛直分布が対数則に従うとき、1ラン30分観測の合計259ランから、さらに条件を 厳選した175ランから得た値として、k=0.39±0.03であり、乱流の性質から標準 偏差7%のばらつきを持つことを発表した(Kondo and Sato, 1982)。 超音波風速計はプローブ(直径2cmほどの棒形状の音波の発信・受信部)自体が 風の場を変形させ乱流統計量の測定誤差を生じ、その他の誤差もある。プローブは まったく同一形に作ることはできないので、風向によって真の風が歪む。 また、風杯式風速計は風速が弱くなるときの時定数が強くなるときの時定数より大きい 特性をもち、乱流中では平均風速を強めに観測するという避けがたい誤差がある。 通常、多くの者はこれらを補正しないが、私たちは補正して結果を得たのであり、 世界中でもっとも正確な値だと思っている。 それ以後、k=0.35 の主張は消え去ってしまった。 その後Garratt and Taylor(1996)による、世界中で行われたカルマン定数に関する 論文のまとめによれば、大部分がk=0.37~0.41の間にあり、私たちのk=0.39は ちょうど真ん中に入っていることがわかった。 |
|
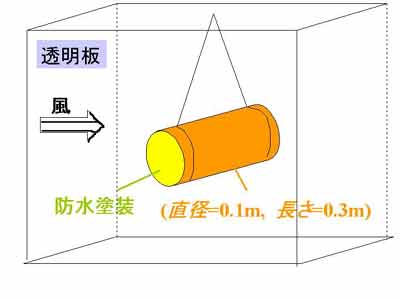
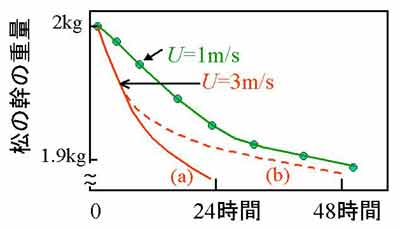
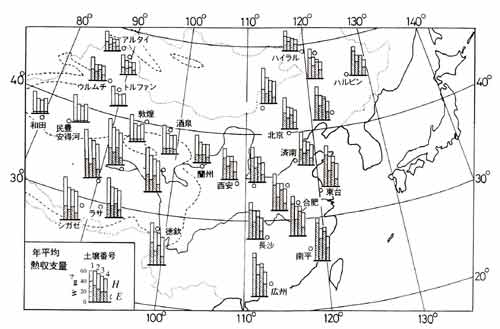
水収支に関するプロジェクト研究 この時代、中国の砂漠地域の水収支に関するプロジェクト研究が開始される状況に あったが、乾燥地の蒸発量の評価方法はできておらず、私は参加せずに準備研究を していた。上記のことからヒントを得て、砂漠など裸地の土壌粒子・大気間の熱・ 水分輸送過程のモデル化を行った(Kondo et al. 1992; Kondo and Saigusa, 1994)。 この計算モデルを中国全域に応用し、通常の気象観測資料を用いる「熱収支法」で 熱収支の時間変化を数値計算し、顕熱輸送量と蒸発量の季節変化と年間量を求める ことができた。土壌の水分パラメータにより結果は異なるので、代表的な4種類 の土壌について計算した(Kondo and Xu, 1997)。 |
|
河川再改修の提案が実行されたかの確認 再改修がどのように行われたかを確認するために、13年後の2007年10月22日、 その後の秋山沢川の状況を視察した。再改修によって造られた2~3m幅の溝(水路) があり、低水時の河川水はこの水路を流下していた。 |

|
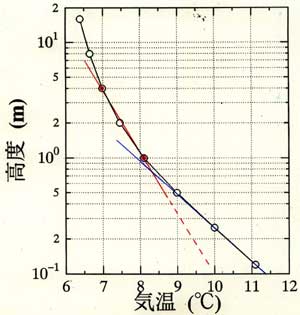
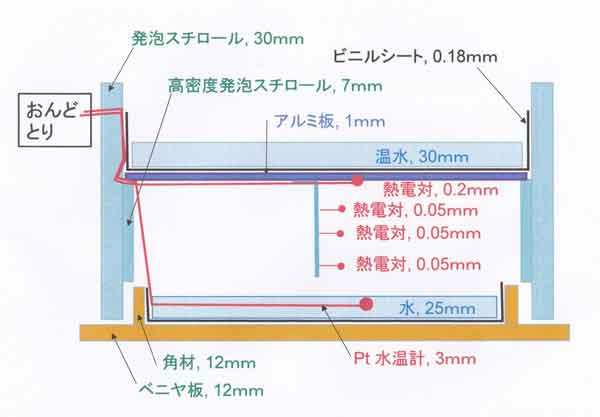
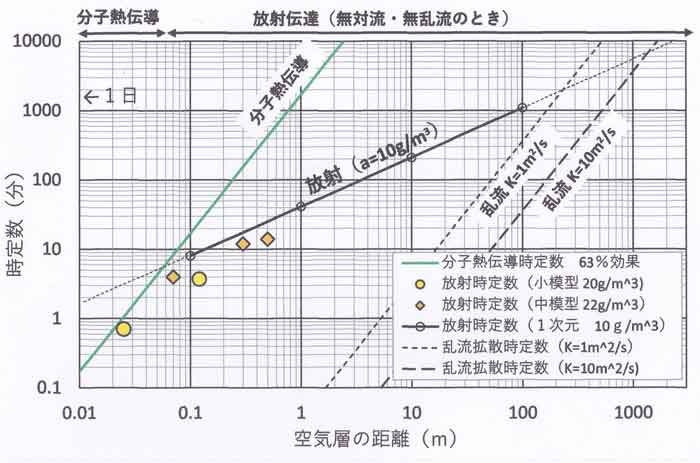
理論式から外れた実験値についての検討 空気層の距離z=0.025mのプロットが式(3)の線から大きく外れており誤差にしては 大きすぎる。ここで、理論計算は放射のみを考えたことに気づいた。外れのz= 0.025mでは分子熱伝導が効いているのではないか、と疑ったことが面白い結果を 導くことになる。 熱伝導のときは次の理論式で表される( 「K191.空間内の温度に及ぼす放射影響の実験(2)」)。 時定数:τ=Bz2 (4) 分子熱拡散係数K=2.1×10-5m2/sのとき、 B=1700分/m2 となる。外れたz=0.025mに対するプロットは式(4) とほぼ重なっており、外れたプロットの理由に納得できた。さらに(スライド㉝) 「K208」第2図から、水蒸気量=10g/m3 のときは空気幅0.06mを境にして、 これ以下なら伝導熱、以上なら放射の役割が大きいことが分かる。 これを盆地の下層大気にあてはめてみよう。下層雲の雲底が高度100mにあり、 その下に地表面温度と異なる高温空気が移流してきたとき。大気は安定成層で 乱流が働かないとする。100mの空気層の放射時定数は1050分(17.5時間)で あるので、移流暖気は17.5時間でほぼ消滅することになる。これは図に示す 水蒸気量が10g/m3 の場合である。水蒸気量がこれより多い場合は、 放射の作用が大きくなり放射時定数は短くなり、より短時間で移流暖気は消滅する。 続いて乱流がある場合を考えよう。乱流拡散係数K=1m2/s の場合は 地面からの概略高度z<200mでは乱流の効果が放射の効果より大きく作用するが、 概略z>200mでは放射の作用が上回る。大気の平均的状態である概略値 K=10m2/s の場合、大スケール(地球規模)に近づくほど放射の 作用が大きくなる。つまり,地球大気の平均的な温度分布や気候変化は基本的 に放射の作用によって決まってくる。このことが再認識できたのである。 教訓として、先入観・常識から外れた実験結果があったとき、誤差として捨てず、 外れの原因を考察しよう。論文の中には、外れたプロットを捨てて著者の先入観に 合致した図を公表している例がある。 |



| トップページへ | 研究指針の目次 |